Метод токов связей (контурных токов)

Вначале, на примере графа (рис.5.4), покажем справедливость следующего равенства:

представляющего собой связь между токами ветвей и контурными токами. Здесь [Ik] - матрица контурных токов, элементами которой являются контурные токи (токи ветвей связи), число которых равноnв = nв - nу +1

Для графа (рис. 5.4)с использованием контурной матрицы (5.10) получим

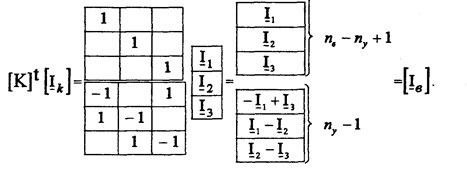
Первые nв - nу +1 строк полученной матрицы отражают в себе тот факт, что контурные токи равны токам связей. Остальные nу -1 строк определяют токи деревьев

по уравнениям ЗТК, записанным для главных сечений. Следовательно, после перемножения получается матрица токов ветвей.

Напомним, что в уравнениях контурных токов переменными являются ток связей. Для получения таких уравнений воспользуемся (5.13). Умножим все члены

этого равенства слева на матрицу [ К] и учтем, что

Теперь исключим из последнего выражения токи ветвей (выразим их через контурные токи) при помощи (5.15) и получим окончательно

представляющее собой матричное уравнение контурных токов. Правая часть (5.16) учитывает все источники ЭДС и токов, действующих вцепи. В левой части тройное матричное произведение

представляет собой матрицу контурных сопротивлений [Zk] . Действительно, для примера (рис 5.4), используя (5.10) и учитывая, что

Расчет цели методом контурных токов выполняется в следующем порядке: в

начале по (5.1 б) вычисляется матрица контурных токов [Ik], а затем по (5.15) - токи [Ik]

ветвей [Iв] Обычно для этих вычислений используются стандартные программы ЭВМ и некоторых отечественных программируемых калькуляторов.

5.4. Метод узловых напряжений

Покажем вначале на примере справедливость следующего матричного равенства

Равенство (5.17) устанавливает связь между напряжениями ветвей и узловыми напряжениями при условии, что базисный узел выбран за опорный.

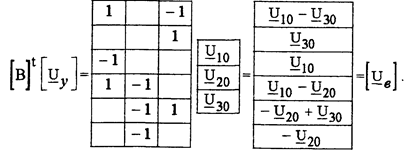
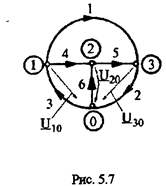
Для графа схемы (рис. 5.1 и 5.7), используя полученную ранее матрицу [ В], при базисном узле 4 имеем

Каждая строка полученной матрица определяет напряжение соответствующей ветви через узловые напряжения по ЗНК.

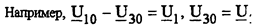
т.д. Следовательно, она является матрицей

напряжений ветвей [Uв] . Для записи

матричного уравнения узловых напряжении воспользуемся уравнением ветви форме (5.4) и умножим его

на матрицу[ B] слева. Учтем также, что

Исключим теперь напряжения ветвей [Uв ] при помощи (5.17) и получим окончательно

представляющее собой уравнение узловых напряжений в матричной форме Правая часть (5.18) учитывает источники токов и преобразованных

источников ЭДС. Тройное матричное произведение

в левой

части равно матрице контурных проводимостей схемы. Для схемы рис. 5.7 в этом не трудно убедиться, если воспользоваться полученными выше [B] и [B]^е, а так матрицами учесть, что

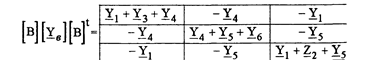
По методу узловых напряжении расчет выполняется порядке следующем:

вначале определяются узловые напряжения [Uy] (из 5.18), затем матрица напряжений ветвей по (5.17), а потом матрица токов ветвей из (5.14).

5.5. Метод напряжений ветвей дерева

Учитывая аналогию уравнений ЗТК через матрицу вершин[В] [Iв]=0 и матрицу сечений [ C][Iв] = [ 0], можно получить уравнение, аналогичное матричному уравнению узловых напряжений (5.18), заменив в нем матрицу вершин| В| на

матрицу сечений[С ]. При этом количество независимых переменных nу -1 не

изменится, а в качестве переменных будут использоваться не узловые напряжения, а напряжения ветвей выбранного дерева графа. Действительно, если

, то аналогичное уравнение, записанное через матрицу сечений

столбцовая матрица напряжений ветвей дерева.

В качестве примера запишем уравнение (5.19) для графа (рис. 5.8) с использованием матрицы [С ], записанной ранее (5.5)

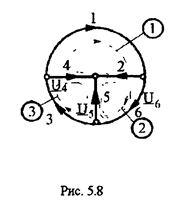
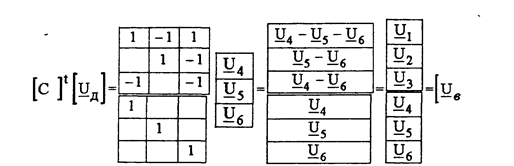
Первые три строки полученной матрицы - напряжения 1,2 и 3 ветвей связи, определяемые по уравнениям ЗНК, записанных для главных контуров 1,2 иЗ (рис 5. Остальные строки тривиально определяют напряжения ветвей дерева.

Используя уравнения (5.6) (5.14) и (5.19), получим уравнение, аналогичное уравнению узловых напряжений (5.18)

которое называется матричным уравнением напряжений ветвей дерева. Вычисление токов ветвей [Iв ] осуществляется аналогично методу узловых

напряжений.

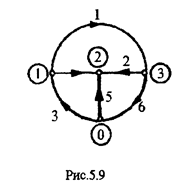
Уравнения узловых напряжений и напряжений ветвей дерева аналогичны и совпадают в том случае, если все ветви графа имеют общую точку, и она выбрана в качестве опорного узла (о) (рис. 5.9).

Основные определения, понятия. Законы коммутации.

Переходные процессы возникают в электрических цепях при переходе из одного режима в другой в следствие подключения источников в сеть, отключения от нее, изменения параметров сети или ее топологии. Любая причина, вызывающая переходный процесс, называется коммутацией.

В большинстве случаев переходные процессы возникают после срабатывания механического или электронного переключателя, работу которого сопровождают весьма сложные явления - горение дуги, перенос носителей в полупроводнике, пробой изоляции и другие- Учет всех этих факторов представляет собою трудную и часто практически неразрешимую задачу. Поэтому при анализе переходных процессов реальное устройство представляется схемой замещения, отражающей рассматриваемые физические процессы с достаточной для практики точностью. В результате получают идеализированную расчетную модель цепи, содержащую сосредоточенные параметры - активное сопротивление, индуктивность, емкость, взаимную индуктивность и идеализированный ключ мгновенного действия. Предполагается, что процесс переключения таким ключом совершается мгновенно за время Dt->0, в течение которого его сопротивление изменяется мгновенно от бесконечности до нуля при включение и от нуля до бесконечности - при выключение.

Задача исследования переходных процессов состоит в определение в мгновенных значений напряжений U(t), токов i(t), потокосцепдений y(t)

и т.п. после коммутации. Обычно момент коммутации совмещается с началом отсчета времени t =0. Момент времени непосредственно предшествующий коммутации обозначают t = 0^- и непосредственно после

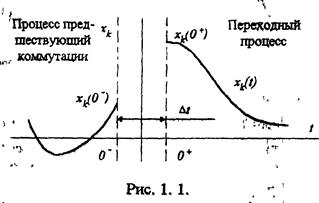
На рис. 1. 1 представлена кривая некоторой переменной напряжение тока и т.п.) хk(t) до и после коммутации. Расчету подлежит функция x_k(t) при t>=0⁺ . Она определяется, как решение системы

интегродифференциальных уравнении цепи образующихся после коммутации, с учетом состояния цепи, предшествующего коммутации x_k(0^-).

Классический метод анализа переходных процессов состоит в формирование и последующем решение системы обыкновенных линейных дифференциальных уравнений цепи. Они должны составляться для цепи

после коммутации на основе законов Кирхгофа или с применением методов токов связей, узловых напряжений с использованием уравнений элементов, приведенных в табл1.

Таблица 1 Уравнения элементов

Затем полученные уравнения необходимо привести к одному

дифференциальному уравнению относительно искомой переменной.

порядка, линейное с постоянными коэффициентами:

(Неоднородное уравнение, так как правая часть f(t)¹0).

Как известно из математики решение неоднородного уравнения складывается из двух решений:

x(t)=х'(t)+х"(t), (2)

где х'(t) = хуст(t)-частное решение неоднородного уравнения, которое в

электротехнике носит понятие установившейся (вынужденной ) составляющей;

x"(t) = x_св(t) -общее решение однородного дифференциального уравнения

Составим характеристическое уравнение. Для этого необходимо первую производную заменить на a, вторую- a², а n- производную на aⁿ B соответствии с выражением (2) имеем

Решая (3), найдем корни характеристического уравнения. Свободная составляющая всех реакций с течением времени затухает, так как энергия электрических полей емкостей и магнитных полей индуктивностей цепи убывает при выключенных источниках. Как видно из (3), для этого необходимо, чтобы вещественные части всех корней характсристического уравнения были отрицательны Re[ak]<0, т.е. корни должны быть либо отрицательными вещественными, либо комплексными сопряженными с отрицательной вещественной частью.

то, если во время коммутации L=const, то чтобы не изменилась энергия достаточно, чтобы

то есть ток в индуктивности во время-коммутации скачком измениться не может( ток в индуктивности до коммутации равен току индуктивности после коммутации). Условие (4) выражает закон коммутации тока в индуктивности. Если во время коммутации меняется величина индуктивности, то необходимо рассматривать более общий закон коммутации, гласящий ,что потокосцепление контура во время коммутации скачком измениться не может:

Энергия электрического поля емкости как известно, равна

Поэтому имеем следующий закон коммутации для емкости:

напряжение емкости во время коммутации скачком изменится не может(напряжение на емкости до коммутации равно напряжению емкости после коммутации). В случае, если емкость меняется во время коммутации, то говорят о более общем законе: заряд узла, содержащего емкости, скачком изменится не может

После определения свободной и установившейся составляющих окончательно записывают решение дифференциального уравнения в соответствии с выражением (2).

В некоторых случаях для оценки сложности решаемой задачи представляет интерес определение, порядка цепи n. Как известно из курса математики, порядок цепи (порядок системы дифференциальных уравнений) равен числу независимых начальных условий. Отсюда следует, что порядок цепи может быть определен по числу независимых начальных условий.

Так как напряжения на индуктивностях

и токи в емкостях определятся первыми производными по времени, то наибольший порядок цепи равен суммарному числу индуктивностей и емкостей, включенных в цепь. Обозначим это число NLC. Однако индуктивности и емкости могут соединятся между собой так, что их начальные токи и напряжения окажутся зависимыми. Рассмотрим сечение цепи, которое включает в себя только ветви с индуктивностями и с источниками тока (рис. 2).

По ЗТК для него можем записать уравнение в момент времени t-=0⁺из которого следует, что

одно т начальных условий является зависимым и такая подцепь имеет порядок не третий (по числу индуктивностей), а второй. Такое сечение, содержащее только ветви с индуктивностями и с источником тока, называют индуктивным. Еслицепь содержит NLI таких сечений, то порядок цепи n=NLC-NLI

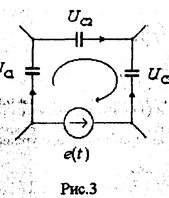
Рассмотрим контур схемы, состоящей из емкостей и источников напряжения, изображенный на рис.3, и запишем для него уравнение ЗНК

в момент времени t=0⁺

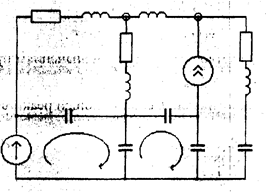
В качестве примера определим порядок цепи, изображенной на рис. 4. Здесь имеем N_LC=9, два емкостных контура и два индуктивных сечения, указанных на рисунке. Поэтому получим n =9-2-2=5. Заметим, что порядок цепи может оказаться меньше, чем вычисленный по (10) вследствие определенного соотношения параметрами схемы.