Рассмотрим мощность в цепи несинусоидального тока.

Пусть напряжение и ток разложены в ряд Фурье:

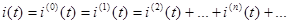
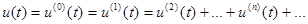
Тогда мгновенная мощность равна

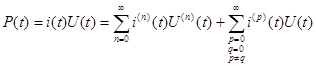(4.5)

Пользоваться понятием мгновенной мощности неудобно, так как она зависит от времени.

Найдем среднюю мощность за период, т.е.активную мощность:

,

где 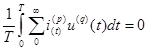(в силу ортогональности гармонической функции)

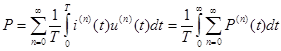б

где 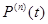-мгновенное значение мощности ‘n’-ой гармоники,

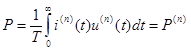-среднее значение (активная мощность) ‘n’-ой гармоники

тогда с учётом последнего получим:

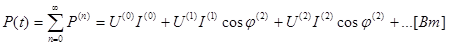(4.6)

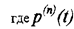
Активная мощность в цепи несинусоидального тока равна сумме активных мощностей каждой из гармоник в отдельности.

Кроме понятия активной мощности рассматриваем понятиеполной мощности

где ????????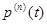

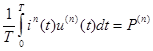
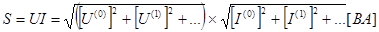(4.7)???????

и реактивной мощности:

(4.8)????????

Последняя равна алгебраической сумме реактивных мощностей каждой гармоники. Отношение активной мощности к полной называетсякоэффициентов мощности:.

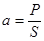коэффициент мощности.

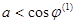-т.е. а всегда меньше COS(фи) для основной гармоники

Активная мощность в цепи несинусоидального тока больше активной мощности в цепи синусоидального тока за счет наличия дополнительных высших гармоник.

В цепи несинусоидального тока присутствует такжемощность искажений

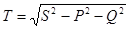(4.10)

которая получается в силу разного гармонического состава кривых тока и напряжения.

Для оценки формы кривых напряжения и тока используется ряд коэффициентов, при этом рассматриваются кривые, в которых отсутствует постоянная составляющая.

Коэффициент формы определяется как отношение действующего значения к среднему за период:

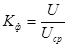
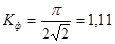(4.11)

для синусоиды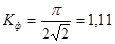

Коэффициент амплитуды равен отношению максимального значения к действующему:

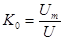(4.12)

для синусоиды ,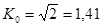

Коэффициент гармоник характеризует совокупную величину высших гармоник и равен отношению действующего значения высших гармоник к действующему значению основной:

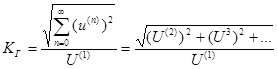(4.13)

По стандарту для промышленной сети коэффициент гармоник не должен превышать 5%.

5. Матричный метод анализа цепей 5.1. Законы Кирхгофа в Матричной форме

При анализе сложных электрических цепей целесообразно использовать матричный метод, основанный на представлении топологии цепи и ее параметров таблицами чисел - матрицами. Матричный метод позволяет записать уравнения цеп наиболее компактных форме, а также систематизирует и упрощает процесс их формирования. Достоинства матричного метода особенно проявляются при использовании ЭВМ, так как он позволяет получить алгоритмы формирования уравнений цепей и упростить их решение на ЭВМ.

Матричный метод базируется на классической теории цепей и опирается на законы

Кирхгофа, справедливые для любых цепей (линейных и нелинейных) с сосредоточенными параметрами.

Уравнения закона токов (ЗТК) и закона напряжений (ЗНК) Кирхгофа определяются только схемами соединения ветвей и не зависят от их физического содержания. Поэтому для записи уравнений Кирхгофа в матричной форме достатоно¹ располагать только направленным графом схемы и представить его, а также выбран переменные (токи и напряжения ветвей) в виде матриц.

Важным требованием, предъявляемым к уравнениям цепи, является их независимость - ни одно уравнение системы не должно являться линейной комбинацией остальных уравнений. Получение линейно независимых уравнений цепи как в классической так и в матричной формах обеспечивается применением теории графов, являющейся частью математической дисциплины - топологии (см. подразд. 2.4).

5.1.1.Закон токов Кирхгофа. Матрицы вершин и сечений

Уравнение ЗТК для i - го узла (сечения) можно представить в следующем

виде:

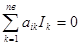k=1,2….

где коэффициент аik = + I, если k-я ветвь выходит из i -го yзла; аik = -I, если она входит в i -и узел и аik = 0, если k -я ветвь не соединяется с i -м узлом.Отметим, что число слагаемых в уравнении (5.1.) всегда равно числу ветвей схемы nв .

Если записать уравнения ЗТК для всех ny узлов, то получим систему следующего вида:

для синусоиды

Коэффициент гармоник характеризует совокупную величину высших гармоник и равен отношению действующего значения высших гармоник к действующему значению основной:

По стандарту для промышленной сети коэффициент гармоник не должен превышать 5%.

5. Матричный метод анализа цепей 5.1. Законы Кирхгофа в Матричной форме

При анализе сложных электрических цепей целесообразно использовать матричный метод, основанный на представлении топологии цепи и ее параметров таблицами чисел - матрицами. Матричный метод позволяет записать уравнения цеп наиболее компактных форме, а также систематизирует и упрощает процесс их формирования. Достоинства матричного метода особенно проявляются при использовании ЭВМ, так как он позволяет получить алгоритмы формирования уравнений цепей и упростить их решение на ЭВМ.

Матричный метод базируется на классической теории цепей и опирается на законы

Кирхгофа, справедливые для любых цепей (линейных и нелинейных) с сосредоточенными параметрами.

Уравнения закона токов (ЗТК) и закона напряжений (ЗНК) Кирхгофа определяются только схемами соединения ветвей и не зависят от их физического содержания. Поэтому для записи уравнений Кирхгофа в матричной форме достатоно¹ располагать только направленным графом схемы и представить его, а также выбран переменные (токи и напряжения ветвей) в виде матриц.

Важным требованием, предъявляемым к уравнениям цепи, является их независимость - ни одно уравнение системы не должно являться линейной комбинацией остальных уравнений. Получение линейно независимых уравнений цепи как в классической так и в матричной формах обеспечивается применением теории графов, являющейся частью математической дисциплины - топологии (см. подразд. 2.4).

5.1.1.Закон токов Кирхгофа. Матрицы вершин и сечений

Уравнение ЗТК для i - го узла (сечения) можно представить в следующем

виде:

где коэффициент аik = + I, если k-я ветвь выходит из i -го yзла; аik = -I, если она входит в i -и узел и аik = 0, если k -я ветвь не

соединяется с i -м узлом.

Отметим, что число слагаемых в уравнении (5.1.) всегда равно числу ветвей

схемы nв .

Если записать уравнения ЗТК для всех ny узлов, то получим систему следующего вида:

которую легко записать в матричной форме. Для этого обозначим матрицу коэффициентов размером (ny nв) через[Во] и столбцовую матрицу токов [Iв] Тогда (5.2) примет следующий вид:

[Bo][lв]=0. (5.3) Матричное уравнение (5.3) выражает уравнение ЗТК для всех узлов схемы

Матрица [bo ] называется полной матрицей вершин, a[Iв] - матрицей токов ветвей.

Для примера запишем матрицы [bo ] и [Iв] для графа, изображенного на рис 5 1. и имеющего nу =4, nв =6.

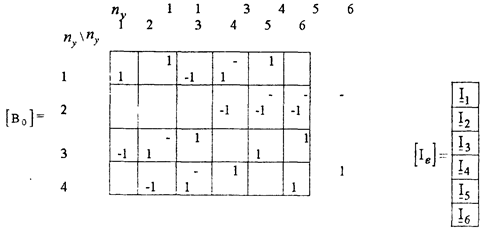
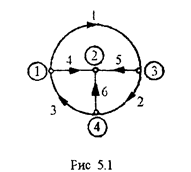
Оставшаяся после удаления базисной строки матрица размером (i

1)хnв обозначается [В] и называется

матрицей вершин. Выражение

[B][lв]=[0] (5.4)

представляет собой уравнена ЗТК в матричной форме.

Для графа (рис.5.1.) выбрав базисным узел 4, получим:

Уравнения ЗТК приобретают более удобный и упорядоченный вид, если для их записи выбрать не независимые узлы, а главные сечения и условиться о определенной процедуре нумерации ветвей и сечений. При записи матричного уравнения ЗТК выбирают дерево графа, затем нумеруют по порядку: вначале все (!!!ci!!!) от 1 до ( nв - п у +1), а потом ветви дерева от (nв - n у +1) до nв обозначают все

главные сечения, число которых равно (ny -1), и задают их направления, совпадают

с направлениями пересекаемых ветвей дерева Затем аналогично матрице I [B] составляется матрица сечений[ С] размером (п y -1)х nв. Знаки элементов

матрицы [ C] определяются относительно направлений сечений. Если направление ветви совпадает с направлением сечения - записывается +I, если не совпадает - (-I), если ветвь не входит в данное сечение записывается ноль

Составим для примера матрицу сечений для графа рис. 5.2

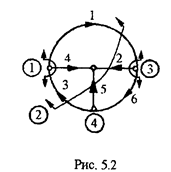
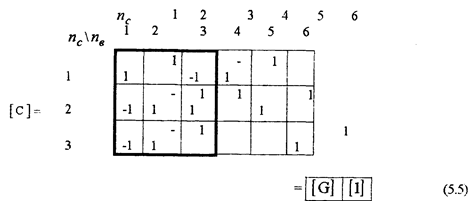
Особенностью матрицы [ С] является то, что ее можно представить в виде двух блоков - матрицы [G] и единичной матрицы размером (ny -1)х(ny -1), как это показано в (5.5.).

Отметим, что матрицы [ G] и [В] содержат полную информацию о графе.

Это означает, что, располагая матрицей [ G] или матрицей [ В], можно восстановить графы схемы.

Умножив матрицу [ С] слева на матрицу токов ветвей[iв ], получим аналогично (5.4) выражение ЗТК в матричной форме

5.1.2. Закон напряжений Кирхгофа. Контурная матрица.

виде

где bik = +I, если направление k -ой ветви совпадает с направлением обхода контура, bik = -1 - если эти направления не совпадают, и bik = 0, если k -я ветвь не входит в i -и контур. Если записать уравнения ЗНК для всех nU =(nв-ny +1) главных контуров

графа, то получим систему уравнений следующего вида:

Левую часть системы уравнений (5.8) удобно представить в виде произведения двух матриц: матрицы коэффициентов bik размером (nв - п y + 1)х nв

виде контурной матрицы [ К] и столбцовой матрицы напряжений ветвей[Uв ]:

Последнее равенство (5.9) представляет собой выражение ЗНК в матричной

форме.

При составлении матрицы [ К] для упорядочивания ее элементов следует придерживаться следующего порядка: вначале выбирается дерево графа и производиться нумерация ветвей в прежнем порядке - в начале связи, а потом ветви дерева, затем по порядку (по номерам связей) обходятся главные контуры в направлениях связей.

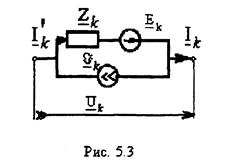
Напомним, что под Uk, понимается напряжение k -и ветви, т.е. условно

выделенного в общем случае активного двухполюсника, или напряжение на зажимаx обобщенной ветви, как это показано, например, на рис. 5.3.

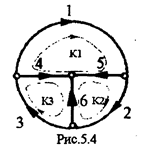
В качестве примера составим матрицы [К] и [Uв ] для графа, изображенного

на рис.5.4 и содержащего nв =6 и ny=4. Поэтому [К] имеет размер 3х6, а[Uв] -6х1:

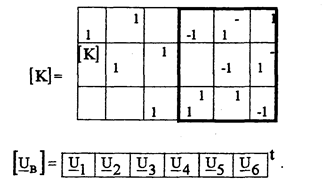
Общим свойством матрицы [К], которое является следствием выбранной процедуры ее составления, является то, что она всегда содержит блок в виде

единичной матрицы[1св] размер которой равен числу связей. Остальную часть матрицы [ К] обозначим [ F], и тогда контурная матрица

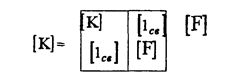
5.2.Уравнения ветви. Обобщенная ветвь.

Для сокращения числа уравнений цепи (размеров матриц) и получения наиболее общих результатов, рассмотрим в качестве ветви схему (рис. 5.3), называемую обобщенной ветвью.

Аналитическая связь между током I. и напряжением Uk ветви, выражен

через ее параметры, называется уравнением ветви.

Запишем для обобщенной ветви уравнения по ЗНК и ЗТК

и подставив второе уравнение в первое, получим выражение

представляющее собой уравнение к -и ветви.

Заметим, что если ветвь не содержит источников (источник тока разомкнут источник ЭДС замкнут накоротко), то получим

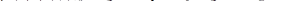
Для схемы, содержащейnв не связанных между собой ветвей, мы можем записать

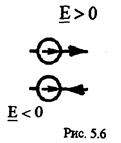
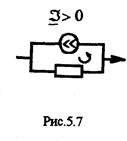
следующих правил знаков. Если направление ветви совпадает с направлением ЭДС, она записывается со знаком плюс, а если эти направления не совпадают - минус

(рис. 5.5). При определении знака источника рассматривается контур, составленный из источника и параллельной ветви.

Этот контур обходят в направлении этой ветви (рис. 5.6). Если выбранное направление обхода контура совладает с 3, то его записывают со знаком плюс, и если не совладает - со знаком минус.

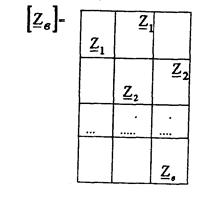
Равенство (5.13) можно решить также относительно токов:

Равенство (5.13), также как и (5.14), являются уравнением ветви. Иногда их называют уравнениями закона Ома в матричной форме.