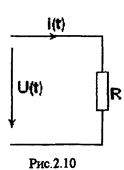
Активное сопротивление в цепи гармонического тока.

Пусть активное сопротивление R включено на источник гармонического напряжения и для какого-то времени укажем направление тока, и напряжения. Допустим ток в цепи равен:

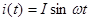
Тогда напряжение и = iR (закон Ома для мгновенных значений), равно

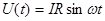
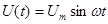
где Um=ImR- амплитудное значение напряжения.

Сопоставляя выражения для тока и напряжения, видно что на активном сопротивлении ток i(t) и напряжение u(t) совпадают по фазе, начальные фазы

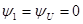и угол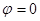

Векторная диаграмма - это графическое изображение векторов токов и напряжений в пели на комплексной плоскости . Диаграмму рисуют относительно комплексных амплитуд (либо комплексов действующих значений) - см.рис.2.11

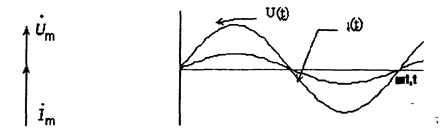
Рис 2 11 Векторная ^{рис 2}.¹² Временные зависимости тока

диатрамма ветви с активным и напряжения в ветви с активным

сопротивлением сопротивлением

Найдем как связаны ток и напряжение на активном сопротивлении. На основе МКА запишем: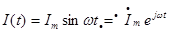

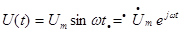
Из закона Ома: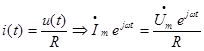

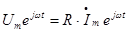
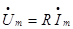
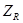-комплексное сопротивление цепи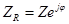

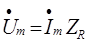
2.6. Индуктивность в цепи гармонического тока.

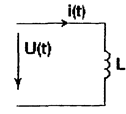
Пусть индуктивность включена на источник синусоидального тока.

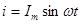
Тогда напряжение на индуктивности:

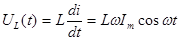(2)

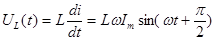
Как видно из (2) напряжение на индуктивности uL(t) по фазе опережает ток на угол 90° (пи/2), т.е. ток в индуктивности отстает от напряжения на 90°.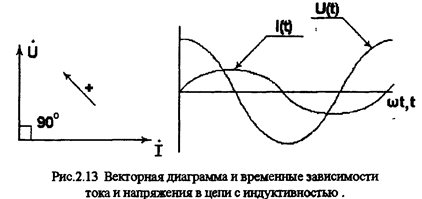

Обозначим

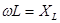-реактивное сопротивление индуктивности

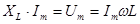-Закон Ома для амплитудных значений

Тогда из (2) с учетом введенных обозначений -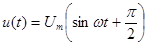

Используя МКА, найдем как связаны комплексы амплитудных значений тока и напряжения на индуктивности.

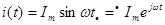
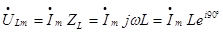
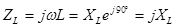-комплексное сопротивление индуктивности

Найдем проводимость индуктивности

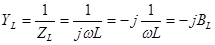-комплексная проводимость индуктивности

где 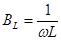-реактивная проводимость индуктивности .

2.7.Емкость в цепи гармонического тока.

Пусть емкость С включена на источник синусоидального напряжения.

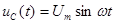(1)

Найдем ток емкости в соответствии с выражением

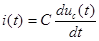
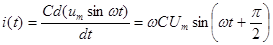
Построим кривые зависимостей тока и напряжения емкости:

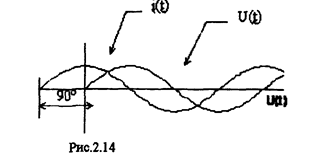
Как видно из рис.2.14 и выражения (3), ток в ёмкости на 90° опережает напряжение.

Перейдем от выражений (1)-(3) к комплексным амплитудным значениям тока и напряжения.

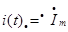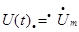; (4)

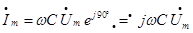(5)

Обозначим величину ,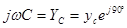

где 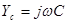-комплексная проводимость ёмкости.

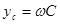-реактивная проводимость ёмкости.

Тогда имеем ,

Найдем сопротивление емкости

,

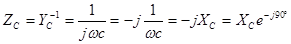где 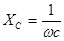-реактивное сопротивление ёмкости,

Сопротивление Zc - величина, обратная проводимости. Yc. Изобразим векторную диаграмму

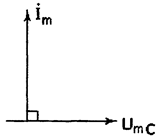
Рис.2.15 Векторная диаграмма тока и напряжения в цепи с емкостью. 2.7.