Анализ сложных цепей по законам Кирхгофа.

Рассмотрим, как записывается законы Кирхгофа для комплексных амплитуд.

Как известно для мгновенных значений

ЗТК: 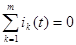(1)

На основе свойства линейности метода комплексных амплитуд ЗТК для комплексных амплитуд будет выглядеть следующим образом

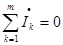(2)

и читается: алгебраическая сумма комплексов амплитудных (действующих значений) тока в узле (сечении) равна нулю.

Закон напряжений Кирхгофа для мгновенных значений

ЗНК: 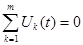(3)

Аналогично на основе свойства линейностиимеем

ЗНК: 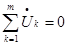(4)

Алгебраическая сумма комплексов амплитудных (действующих значений) напряжений в контуре равна нулю.

Так как формально законы Кирхгофа выглядят аналогично законам Кирхгофа для цепи постоянного тока, то для расчета цепей переменного тока могут быть использованы все ранее рассмотренные методы расчета цепей: МТС, МУН, МНД и др.

Однако, следует отметить, что использование МУН имеет особенности ( его не всегда можно использовать, см.Трансформатор)

Рассмотрим цепь с последовательным соединением R, L, С (см. рис. 2.16)

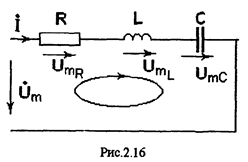
В соответствии с ЗНК имеем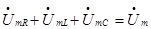

Выразим входное напряжение через ток в цепи:

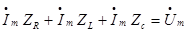
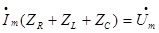
Обозначим :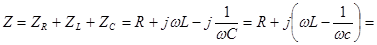

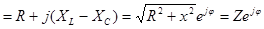
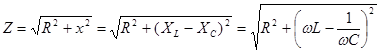
Z - полное сопротивление цепи (модуль комплексного сопротивления)

где х = xl - Хс реактивное сопротивление цепи.

Построим векторную диаграмму. Пусть для определенности ХL > Хc

Характер цели индуктивный, так как ток отстает от напряжения на угол ф. При этом соотношение между напряжениями индуктивности и емкости:

;

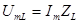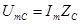
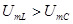
Рис.2.17 Векторная диаграмма для цепи с последовательным соединением R,L,C.