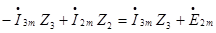Очевидно, что входное сопротивление и проводимость - обратные величины.
Определим, как связаны реактивное и активное сопротивление с активной и реактивной проводимостью.
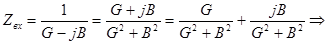
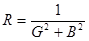 ;
; 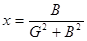
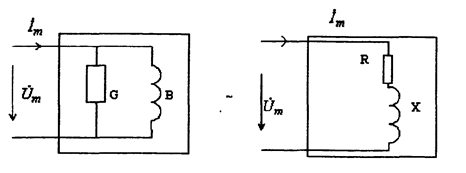
Параллельная схема замещения последовательная схема замещения двухполюсника двухполюсника
Рис.2.21
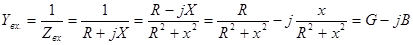
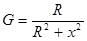 ;
; 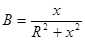 -формулы перехода от последовательной схемы к параллельной
-формулы перехода от последовательной схемы к параллельной
Следует отметить, что зная параметры одной схемы замещения возможно найти параметры другой только при данной частоте, так как в исходной схеме сложной цепи частотные характеристики элементов и ветвей различны.
2.9.Анапиз сложных цепей гармонического тока на основе метода токов связи.
При анализе сложных цепей необходимо от цели, содержащей элементы:
активные сопротивления, емкости, индуктивности, перейти к комплексным сопротивлениям и комплексам амплитудных значений тока и напряжения, затем необходимо перерисовать цепь. Если не обращать внимание на точки и считать, что соответствует R, то для расчета цепей переменного гармонического тока возможно использовать все ранее рассмотренные методы расчета цепей постоянном тока.
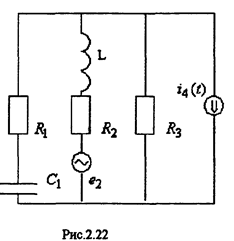
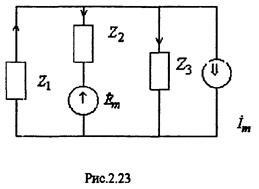
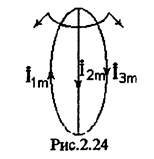
Пример: Составим уравнения для расчета цепи (см. Рис.2.22) по законам Кирхгофа, методом токов связей и узловых напряжений.
|
|
|
|
|
|
Составляем уравнения по МТС:
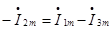
|
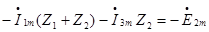
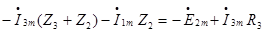
Система уравнений (*) содержит только токи ветвей связи, причем это -иначе записанные ЗНК. Правая часть содержит слагаемые с источниками ЭДС и тока, как в ЗНК, а в левой части записаны падения напряжения от токов ветвей связи.
Обозначим Z11, = Z1 + Z2 - собственное сопротивление 1-ого контура, т.е. сумма сопротивлений ветвей, составляющих 1-й контур.
Z31 = Z13 = Z2 - взаимное (общее) сопротивление цепи, общее для 1 -го и третьего контура.
Для к-го контура с учетом введенных обозначений можно записать
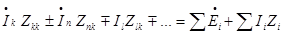
Причем если в его ветвях дерева направления обходов к-го и n-го контура разные, то знак "-". При совладении - знак "+".
Особенности : количество уравнений по МТС равно количеству ветвей связи (p-q+1), если нет топологически вырожденных ветвей, содержащих идеальный источник тока.
Nmtc=p-q+1+n,
где n - число идеальных источников тока.
Дата добавления: 2015-08-21; просмотров: 1399;

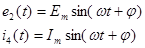
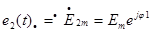
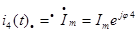
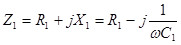
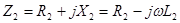
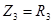
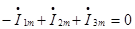 ;
ЗТК:1к:
;
ЗТК:1к: 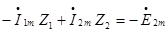 3к:
3к: