Последовательное включение двух индуктивно связанных катушек.
1. Согласное включение.
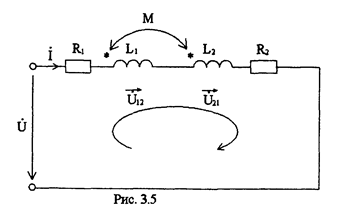
Допустим, катушки соединены согласно, т.е. конец предыдущей катушки соединен с началом следующей, при условии, что они намотаны в одну сторону, ток втекает в одноименные зажимы для первой и второй катушек. Тогда по ЗНК
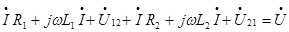 (1)
(1)
| где |
 (2)
(2)
напряжения взаимной индукции на первой и второй катушках. Подставим (2) в (1), получим
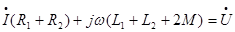 (3)
(3)
Обозначим через 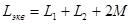 (4)
(4)
индуктивность двух согласовано включённых катушек при их последовательном соединении.
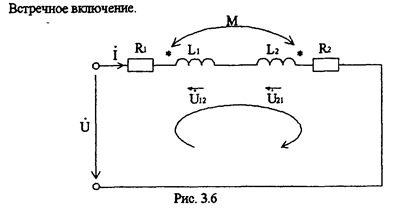
Поменяем у одной из катушек начало и конец (рис. 3.6). Тогда
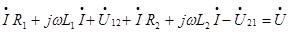
Аналогично найдем эквивалентную индуктивность при встречном включении
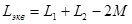 (5)
(5)
Вычитая выражения (4) и (5), определим взаимную индуктивность через эквивалентные индуктивности в виде
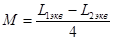 (6)
(6)
• Рассмотрим, как экспериментально определить случаи согласного и встречного включения. Очевидно, что при встречном включении эквивалентное
реакгивное сопротивление Х2зкв =(омега)L2экв получится меньше, чем при согласном
X1экв =(омега)Llэкв, т.к. L1экв >L2экв .Тогда при неизменных параметрах цепи, ток при встречном включении окажется больше, чем при согласном. Теперь можно формулировать правило определения одноимённых зажимов: чтобы экспериментально определить одноимённые зажимы, нужно включить исследуемые катушки и измерить ток; где значение тока выше, там случай встречного включения Величина взаимной индукции может быть найдена экспериментально исходяизвыражения (6).
3.3 Метод холостого хода для определения взаимной индукции.
Для этого необходимо включить первую катушку на источник синусоидального напряжения, и измерить ток в первой катушке и напряжение на второй катушке (см. рис. 3.7).
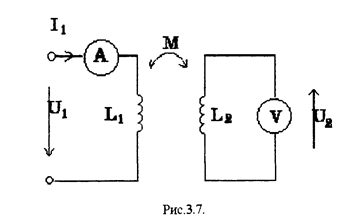
Напряжение на второй катушке равно ЭДС взаимной индукции и определяется выражением
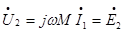
Измерив ток и напряжения можно найти взаимную индуктивность М, исходя из выражения
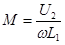
Чем выше сопротивление вольтметра, тем ближе значения напряжения и ЭДС, тем точнее измерение величины взаимной индукции М.
3.4 Анализ сложных цепей с взаимной индукцией.
При анализе сложных цепей произвольно задается направление тока. В зависимости от направления токов относительно одноимённых зажимов, указывают направления напряжений взаимной индукции Затем составляют уравнения для цепи обычными методами расчёта в зависимости от её сложности. Однако, применение метода узловых напряжений для цепи с взаимной индукцией напрямую невозможно Необходимо ввести понятие инверсной индуктивности, либо воспользоваться эквивалентными
схемами замещения, в которых индуктивно связанные контуры
преобразованы в контуры с электрической связью (см Т-образную схему замещении трансформатора)
Например, составим уравнения по ЗНК для контура, положительное направление которого указано по часовой стрелке (см. рис. 3.8). Пусть катушки L1 и связаны взаимоиндукгивно M12=M21. Одноименные зажимы указаны точками (.).
Кроме этого L2 связана с L3, взаимной индуктивностью М23, их одноименные зажимы
на схеме обозначены "(Дельта)".
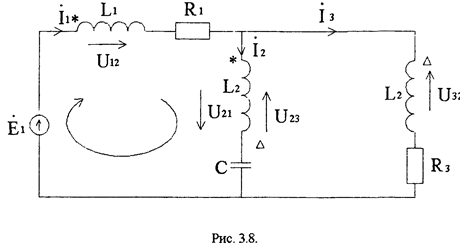
Указывая направления напряжений взаимной индукции и составляя ЗНК, получим:
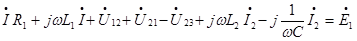
где 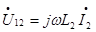 ,
, 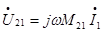 ,
, 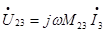
| 3.5. Линейный трансформатор
Трансформатор - это статическое устройство, предназначенное для передачи энергии из одной цепи в другую, с ней электрически hp связанную, т.е. посредством взаимной индукции (магнитного поля).
Трансформаторы содержат две (может больше) катушки (обмотки) с число витков W1 и W2, намотанных на общем сердечнике (см. рис. 3.9). Будем считать, что рабочая точка выбирается на линейном участке кривой намагничивания сердечник т.е. трансформатор линейный
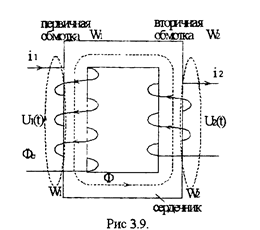
Магнитный поток, который частично замыкается по воздуху, носит название потока рассеяния Фс (см. эквивалентную схему замещения трансформатора рис. 3.9). Поток в сердечнике Ф=Ф12-Ф21, где Ф12 и Ф21 - потоки взаимной индукции, вызванные первичным током I1 и вторичным током II2 соответственно. 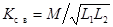
Отсутствие сердечника также обеспечивает линейность характеристик, но приводит к ослаблению электромагнитной связи между катушками, характеризуемой
| коэффициентом связи |
У широко распространенных

трансформаторов с ферромагнитными сердечниками
а без сердечника - 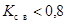
Кроме того, у трансформатора без сердечника на порядок
меньше величины индуктивностей катушек L1 и L2 что приводит к увеличению относительного влияния активных сопротивлений обмоток. Указанные особенности воздушного трансформатора сказывается лишь количественно на его параметрах, не затрагивая существа электромагнитных процессов и характера получаемых зависимостей
Электромагнитные процессы в трансформаторе описываются уравнениями напряжений Кирхгофа, составленными для электрической схемы, приведенной на рис. 3.10:
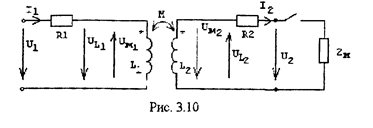
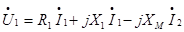 (1)
(1)
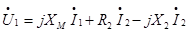
где 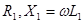 и
и 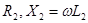 -активные индуктивные сопротивления обмоток
-активные индуктивные сопротивления обмоток 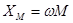 -сопротивление взаимной индукции.
-сопротивление взаимной индукции. 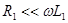
Так как у трансформатора обычно
то для упрощения некоторых
выводов будем пренебрегать R1.
Физический смысл уравнений (1) можно пояснить следующим образом: При подключении первичной катушки к источнику с гармоническим напряжением U1 , возникает переменный ток I1 и обусловленный им переменный магнитный поток самоиндукции. Этот поток индуцирует в витках первичной катушки ЭДС, которая в
первом уравнении (1) учитывается как 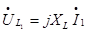 напряжение
напряжение 


 самоиндукции
самоиндукции
Часть этого потока, которая сцепляется с витками второй катушки и называется потоком взаимной индукции, также индуцирует во второй катушке ЭДС, которая учитывается во втором уравнении (1) как 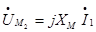 напряжение взаимной индукции
напряжение взаимной индукции
Эта ЭДС является причиной появления на зажимах второй катушки
напряжения U2.
При отсутствии тока I2 (вторичная цепь разомкнута, zh= оо ) режим работы трансформатора называется холостым ходом. Система уравнений (1) принимает вид
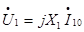 (2)
(2)
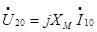
где, I10-ток холостого хода первичной цепи;
U20- вторичное напряжение при холостом ходе. Из равенства (2) (при пренебрежении R1 и R2) получим соотношение напряжений
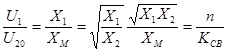 (3)
(3)
где 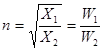 -коэффициент трансформации (4)
-коэффициент трансформации (4)
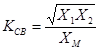 (5)
(5)
У трансформаторов с ферромагнитным 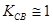 сердечником
сердечником 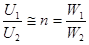
а у трансформаторов без сердечника надо учитывать в формуле (3)
величину Ксв. Отсюда видно, что трансформатор преобразует величину напряжения в зависимости от соотношения числа витков W1 и W2, т.е. коэффициента
трансформации п. При п>1 напряжение понижается, при n<1 - повышается.
В режиме нагрузки, т.е. при подключении к зажимам второй катушки сопротивления Zн(Ha схеме рис.310 ), возникает ток I2 который, в свою очередь, создает свой магнитный поток самоиндукции. Этот поток индуцирует в витках второй катушки ЭДС, которая во втором уравнении (1)учитывается как напряжение
совпадающее по направлению с током I2. Часть потока, созданного, 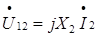
током I2, сцепляется с витками первой катушки (поток взаимной индукции) и индуцирует в них ЭДС. Эта ЭДС в первом уравнении (1) учитывается как напряжение
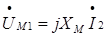
взаимной индукции, которое направлено относительно одноименных
зажимов согласно правилу Ленца так же, как вызвавший его ток I (.)2, т.е. навстречу
напряжению U(.)L1. Поэтому напряжение взаимной индукции входит в первое уравнение (1) со знаком минус. Отсюда следует, что для сохранения равенства (1) т I1 должен измениться, обычно возрасти, в такой степени, чтобы увеличение
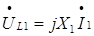 напряжения компенсировало возникшее напряжение взаимной индукции
напряжения компенсировало возникшее напряжение взаимной индукции
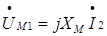 , Значение токаI(.)1 при нагрузке, т.е. при появлении тока I (.)2 может
, Значение токаI(.)1 при нагрузке, т.е. при появлении тока I (.)2 может
быть получена из первого уравнения (1) следующим образом (величиной R1 пренебрегаем): 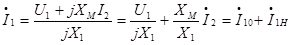 (6)
(6)
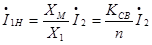 -нагрузочная составляющая первичного тока.
-нагрузочная составляющая первичного тока.
вызванная током нагрузки I2 . Таким образом, при нагрузке в первичном токе к току холостого хода I(.)10
добавляется нагрузочная составляющая I(.)1н обеспечивающая передачу энергии во вторичную цепь. Это можно показать следующим образом:
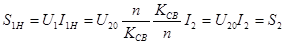 (7)
(7)
Выражение для напряжения на зажимах вторичной цепи при нагрузке может быть получено из второго уравнения (1)

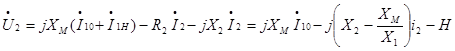 ???????
??????? 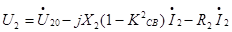 (8)
(8)
Из (8) следует, что изменение U2 при нагрузке обусловлено несовершенной связью и падением напряжения на R2. На величине U2 сказывается также неучтен
падение напряжения R1I1, которое уменьшает U20.
При исследовании цепей с трансформатором последний принято заменять эквивалентной Т-образной схемой замещения. Получим ее уравнения на основе уравнений трансформатора (1). К первому уравнению прибавим и вычтем слагаемое
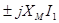 ,а ко второму
,а ко второму 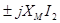 и сгруппируем слагаемые,
и сгруппируем слагаемые,
получим уравнения для Т-образной схемы трансформатора в виде:
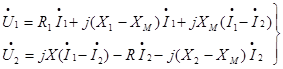 (9)
(9)
Данной системе уравнений соответствует схема на рис. 3.11.
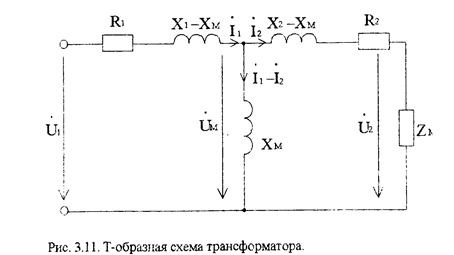
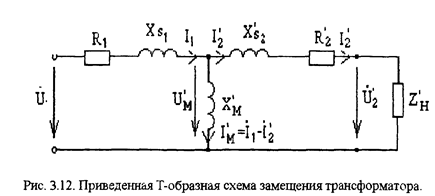
В данной схеме отсутствует связь за счет взаимной индукции вторичной обмотки. Она заменена электрической связью первичного и вторичного контуров за счет сопротивления Хм. Часто используется приведенная Т-образная схема замещения трансформатора (см. рис. 3.12). При этом производится приведение вторичной цепи трансформаторов к первичной, т.е. замена числа витков W2 на W'2 = W1 = nW2. Такое приведение необходимо для того, чтобы избежать появления в эквивалентной схеме отрицательного индуктивного сопротивления (Х1 - Хм ) или
(X2 -Хм ) если Хм > Х1, или Хм > Х2. Для того, чтобы при этом приведении
влияние вторичной цепи на первичную не изменялось, параметры вторичной цепи приведенного трансформатора надо изменять по формулам
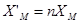
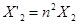
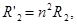
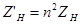 (10)
(10)
Вторичные токи и напряжения в приведенном трансформаторе также будут равны
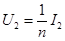
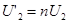 (11)
(11)
При замене приведенными величинами параметров в уравнениях (1) последние примут вид 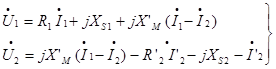 (12)
(12)
Где 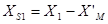 и
и 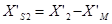 -индуктивные сопротивления.
-индуктивные сопротивления.
рассеяния первичной и приведенной вторичной цепи.
Этим уравнениям соответствует схема замещения, изображенная на рис. 3.12. в этой схеме замещения первичные ток и напряжение такие же, как и в исходном трансформаторе, а вторичные (приведенные) отличаются в 'n' раз согласно формуле (11).
• Пользуясь схемой замещения, очень удобно определять токи и напряжения трансформатора в том или ином заданном режиме. Например, можно задать вторичные ток и напряжение и вычислить первичные. При этом все требуемые величины согласно схеме замещения вычисляются по следующим формулам: 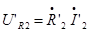 ;
; 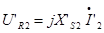 ;
; 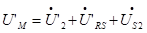 ;
; 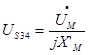 ;
; 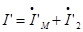 ;
; 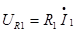 ;
; 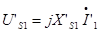 ;
; 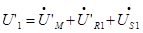 (13)
(13)
Построим векторную диаграмму для приведенного трансформатора. За • исходный вектор примем ток 12, учитывая в зависимости от сопротивления • нагрузки угол сдвига (фи)Н между током и напряжением на нагрузке, строим U(.)2 г, затем падения напряжения на активномI(.)2 R2 и реактивном сопротивлениях рассеивания j • Xs2I(.)2 вторичной обмотки. Сумма этих векторов 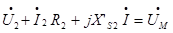 даёт напряжение на индуктивном cопротивлении Х`м контура намагничивания. При этом намагничивающий
даёт напряжение на индуктивном cопротивлении Х`м контура намагничивания. При этом намагничивающий
ток I`(.)м =I(.)1-l`(.)2 отстает от напряжения U(.)м на 90' (ток в индуктивности). За
строим первичный ток трансформатора в соответствии с выражениемI(.)1 = I(.)м-I(.)2
1 откладываем вектор падения напряжения на активном I(.)1R1 и jXs1I(.)1
реактивном сопротивлениях первичной обмотки. Замыкающий вектор определяя
приложенное входное напряженке U(.)1.
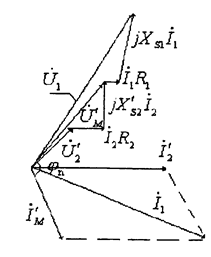
Рис.3.1.3. Векторная диаграмма приведенного трансформатора
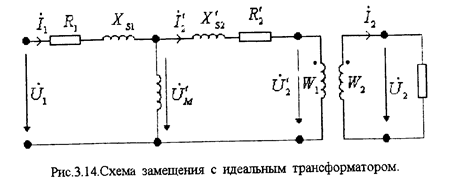
Ввиду того, что вторичные напряжение U(.)2 и ток I (.)2 приведены к первичной обмотке, т.е. изменены пропорционально коэффициенту трансформации -11 (см. формулу .11), то данная схема приведенного трансформатора (рис 3.13) не эквивалентна исходной схеме трансформатора. Для того чтобы она стала эквивалентной заданной, введем, так называемый идеальный трансформатор.
Идеальный трансформатор - это такой трансформатор, у которого -выполняется следующее условие
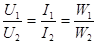 -коэффициент трансформации. (14)
-коэффициент трансформации. (14)
Идеальный трансформатор не имеет потерь энергии- и при разомкнутой вторичной обмотки через его первичную обмотку ток не проходит. Реальный трансформатор будет иметь характеристики идеального, если коэффициент связи
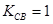 ,
, 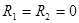 и
и 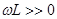 , так что ток холостого хода
, так что ток холостого хода 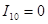
Дополнив схему рис.3.12. идеальным трансформатором, получим эквивалентную схему трансформатора.
Дата добавления: 2015-08-21; просмотров: 12769;
