АНАЛИЗ ЦЕПЕЙ С ВЗАИМНОЙ ИНДУКЦИЕЙ.

3.1 Взаимная индуктивность. ЭДС взаимоиндукции. Маркировка зажимов.

Пусть имеется два контура; первый контур (1к) с числом витков W1, и второй контур (2к) с числом витков W2. Условно покажем каждый из контуров в виде одного витка (см. рис.3.1).

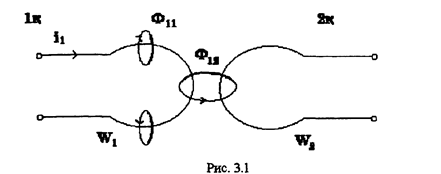
Ток, протекая в первом контуре, создаёт магнитное поле. По правилу буравчика находим направление силовых линий. Силовые линии магнитного потока непрерывны и замкнуты. Некоторые из них будут сцепляться со вторым контуром. На рис.3.1 Ф11 - поток рассеяния, т.е. поток, образованный током первого контура и сцепляющийся с первым контуром. В свою очередь Ф21 - это поток взаимной индукции, т.е. поток, образованный током первого контура и сцепляющийся со вторым. В общем случае индексы у магнитного потока записываются так Фкм - поток взаимной индукции, образованный током М- ого контура и сцепляющийся с витками К- ого контура.

Как известно, под индуктивностью понимают отношение потокосцепления (пси) к току i, его вызвавшему.

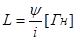
где (пси) =wФ - потокосцепление, w - число витков, Ф - магнитный поток самоиндукции.

Взаимной индуктивностью называется отношение потокосцепления взаимной индукции к току, его вызвавшему.

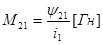(3.1)

где 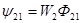, -потокосцепление взаимной индукции.

В линейной цепи взаимная индуктивность не зависит от потокосцепления и тока, а определяется

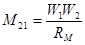(3.2)

где 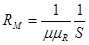-магнитное сопротивление пути замыкания потока взаимоиндукции.

l,S длина и площадь сечения магнитопровода.

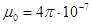
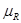-относительная магнитная проницаемость сердечника.

Пусть по второй катушке протекает ток, при этом часть силовых линий магнитного потока будет сцепляться с витками первого контура. Тогда можно ввести потокосцепление взаимной индукции первого контура, вызываемое током второго контура

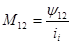. (3.3)

Для линейной цепи выполняется равенство M12=M21=M - принцип линейно' Магнитной цепи.

Всякое изменение магнитного потока во времени порождает ЭДС. Найдем ЭДС взаимной индукции

(3.4)

В соответствии с законом электромагнитной индукции

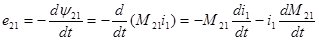
но для линейной цепи М = const и

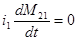
тогда ЭДС взаимной индукции

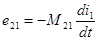(3.5)

ЭДС взаимной индукции уравновешивается напряжением взаимной индукции например, для второго контура

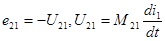(3.6)

В общем случае, ЭДС и напряжение взаимной индукции определяются следующими выражениями: (3.7)

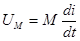(3.8)

Переидём от мгновенных значений к комплексным, получим комплексы амплитудных значений ЭДС и напряжения взаимной индукции.

,

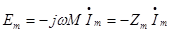
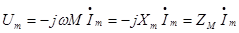где 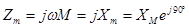-комплексное сопротивление взаимной индукции.

Рассмотрим, как связаны положительные направления тока и напряжения взаимной индукции. Различают так называемые одноимённые (генераторные) зажимы. Это такая пара зажимов, при втекании тока, в которую напряжение взаимоиндукции Um направлено так же, как и токи их вызывающие (см. рис. 3.2). Например, если ток i1 в первой катушке направлен от зажима в катушку, то во второй катушке он наводит напряжение, направленное от зажима в катушку и наоборот, если токi2 во второй катушке протекает по катушке к зажиму, то напряжение в первой катушке направлено также по катушке к зажиму.

В отличие от индуктивности взаимная индукция М может быть больше нуля, меньше нуля, равной нулю.

Рассмотрим все три случая.

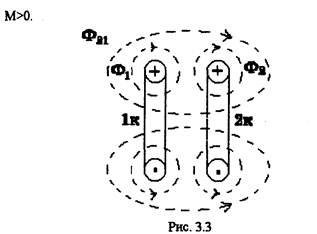
Если поток самоиндукции и взаимной индукции совпадает по направлению катушки включены согласно, при этом взаимная индукция М>0. Например, на рис.3.3

поток самоиндукции Ф2 совпадает по направлению с потоком взаимной индукции Ф

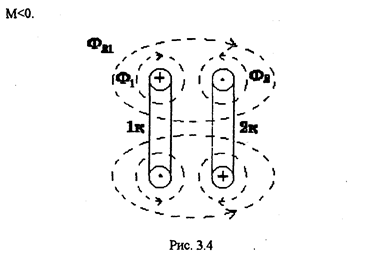
Если потоки самоиндукции и взаимной индукции не совпадают по направлению, имеем встречное включение, при этом М<0 (см. рис. 3.4). Поток Ф2 не совпадает по направлению с потоком Ф21.

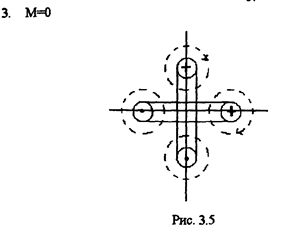
В этом случае оси катушек должны быть взаимно перпендикулярными (см. рис. 3.5).

Маркировка зажимов.

Как определить одноимённые зажимы? Для этого необходимо одну из катушек подсоединить к источнику входного напряжения U1, а вторую катушку одним из концов подсоединить к первой и измерить три напряжения: входное (напряжение на первой катушке), напряжение на второй катушке и общее (см. рис. 3.6). При этом, в зависимости от того какие зажимы катушек соединены, могут встретится два случая. Рассмотрим эти случаи:

1. Предположим, что одноимённые зажимы 1 и 4

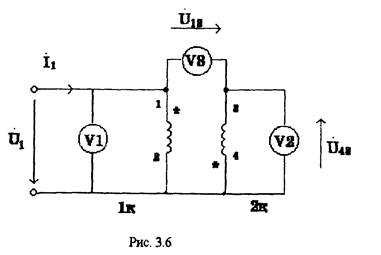
Тогда ток I1 создаёт во втором контуре напряжение взаимной индукции U43 По ЗНК имеем:

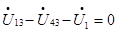(3.1)

или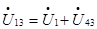

1. Теперь пусть одноимёнными зажимами будут 1-3. При этом напряжение U34 на второй катушке поменяло свое направление

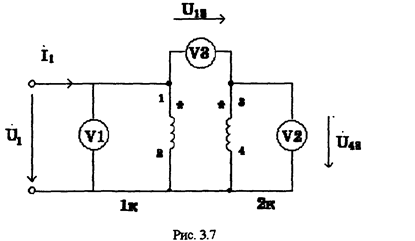
Тогда общее напряжение (3.2)

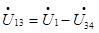
Вывод: если соединяются разноимённые зажимы, то общее напряжение на двyx катушках U(.)13 получается больше входного (первый случай, рис. 3.6). Если

соединяются одноимённые зажимы, то U(.)13 не может быть больше входного (второй случай, рис. 3.7).