Разложение периодической функции в рад Фурье.

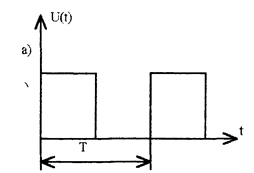
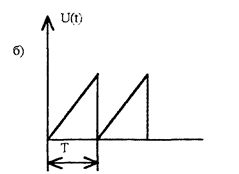
Различные электронные устройства : мультивибраторы, инверторы, трип выпрямители и т.д. , вырабатывают периодические несннусоидальные напряжения различной формы. Например, на рис 4.1 ,а изображена временная диаграмма выходного напряжения триггера, а на рис. 4.1,6—напряжения на отклоняющихся пластин кинескопа.

Рис 4.1

Для расчета цепей при периодических несинусоидальных воздействиях можно воспользоваться принципом наложения . Для этого необходимо представить функцию в виде ряда Фурье .

Как известно из математики, функцияf(t) , удовлетворяющая условию Дирихле , т.е. имеющая на всяком конечном интервале конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть представлен рядом (4,1):

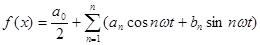
где: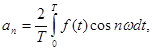

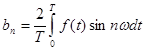
n=0,1,2.....—целое число,

T-период, 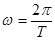-круговая частота.f=1/T ,Гцциклическая частота.

Запишем ряд (2.1) через одну тригонометрическую функцию:

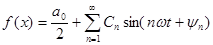(4.3)

где ,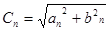

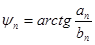
Рассмотрим более подробно слагаемые в выражении (4.3) :

Пусть n=0, тогда из (4.2) имеем:

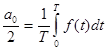-среднее значение функции f(t)за период её изменения (постоянная составляющая функции).

Если n=1, тогда из (2,3) 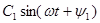представляет собой синусоидальную функцию Её называют основной (первой) гармоникой (тока, напряжения ,ЭДС)

Если n=2, тогда из (2.3) -вторая гармоника (тока, напряжения, ЭДС)

Если рассмотреть 'n' -ое слагаемое получим'n '-ую гармонику, частота

которой в'n' раз выше частоты основной гармоники

Условимся порядковый номер обозначать в верху к круглых скобках, например

если токi(t) разложен в ряд Фурье то его слагаемые следует записать следующем образом:

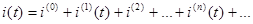
При разложении функции в ряд Фурье необходимо учитывать случаи симметрии кривых: