Взаимная индукция. Взаимная индуктивность

Явление взаимной индукции состоит в том, что при изменении тока в одном контуре возникает наведенная ЭДС индукции в другом, близко расположенном контуре.

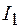Пусть в контуре 1 течет ток (рис. 91.1). 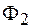– часть потока, созданного током 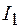и пронизывающего контур 2. Так как 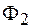~ 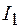, то можно записать:

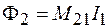, (91.1)

где 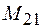– коэффициент пропорциональности, называемый взаимной индуктивностью контуров 2 и 1.

Из формулы (91.1) следует, что взаимная индуктивность контуров 2 и 1 численно равна потоку, пронизывающему контур 2 и созданному током в один ампер, протекающим в первом контуре. Говорят, что между контурами существует магнитная связь. Если ток 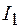изменяется, то в соответствии с выражением (91.1) поток 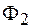, пронизывающий второй контур, также меняется. Но тогда в контуре 2 возникает ЭДС индукции:

. (91.2)

Таким образом, в случае квазистационарности в системе ЭДС индукции в контуре 2 равна

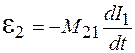. (91.3)

Если изменяющийся ток течет по контуру 2, то, рассуждая аналогично, можно показать, что в контуре 1 при этом возникает ЭДС :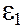

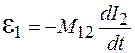, (91.4)

где 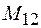– взаимная индуктивность контуров 1 и 2.

Можно доказать, что 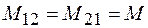. Поэтому говорят о взаимной индуктивности М двух контуров.

Взаимная индуктивность зависит от формы, размеров контуров, их взаимного расположения и магнитной проницаемости среды 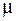, в которой эти контуры находятся. При наличии ферромагнетиков 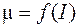. Рассчитаем взаимную индуктивность двух катушек, намотанных на общий сердечник (рис. 91.2). При силе тока 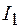в первой катушке полный магнитный поток (потокосцепление), пронизывающий вторую катушку, равен

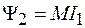. (91.5)

Так как поток, со-зданный первой катушкой, полностью пронизывает и витки второй катушки, то

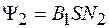, (91.6)

где 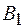– индукция магнитного поля, созданного током .

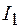Так как индукция магнитного поля 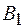определяется выражением

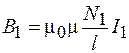, (91.7)

то из сравнения формул (91.6) и (91.7) следует:

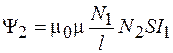. (91.8)

Но тогда из выражений (91.5) и (91.8) для взаимной индуктивности двух катушек получаем:

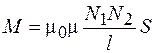. (91.9)

Отсюда видно, что М зависит от размеров сердечника, числа витков катушек и магнитной проницаемости среды.

Умножив и разделив правую часть формулы (91.9) на длину сердечника l, произведем замену 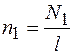, , 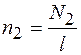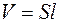и получим другой вариант формулы взаимной индуктивности:

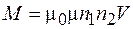. (91.10)

С учетом формулы (74.7) взаимную индуктивность можно выразить через индуктивность каждой из катушек:

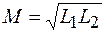. (91.11)