Энергия магнитного поля. Объемная плотность энергии

В результате изучения явления самоиндукции приходим к выводу, что в соответствии с правилом Ленца при размыкании цепи с индуктивностью в ней возникает индукционный ток того же направления, что и основной ток. Следовательно, при размыкании в цепи выделяется джоулева тепла больше, чем это обеспечивает источник тока. Одновременно с выключением тока исчезает магнитное поле. Так как никаких других изменений в цепи не происходит, то можно заключить, что магнитное поле запасает энергию от источника тока, а при отключении источника выделяет энергию в цепь.

При размыкании цепи за время 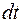током будет совершаться работа

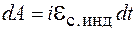, (89.1)

где i – мгновенное значение силы тока; 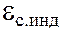– ЭДС самоиндукции.

Подставив в выражение (89.1) вместо 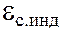соотношение (88.3), получим:

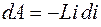, (89.2)

где L – индуктивность цепи.

Проинтегрировав это выражение в пределах от I до 0, получим работу, совершаемую в цепи за все время, в течение которого происходит исчезновение магнитного поля:

.

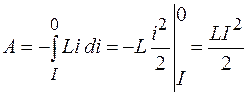Здесь I – сила тока, который протекал в цепи в момент ее размыкания.

В соответствии с вышесказанным работа совершается за счет энергии магнитного поля. Поэтому энергия магнитного поля контура с током равна

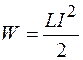. (89.3)

О том, что магнитное поле является носителем энергии, свидетельствует тот факт, что электромагнитные волны, существуя в пространстве без токов, их поддерживающих, переносят энергию.

Подставляя в формулу (89.3) индуктивность соленоида (74.7), получим выражение для энергии магнитного поля соленоида:

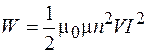. (89.4)

Так как 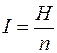, то в соответствии с этим соотношение (89.4) преобразуется к виду

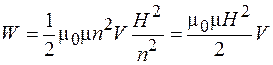. (89.5)

Поскольку магнитное поле соленоида заключено полностью внутри него, то энергия магнитного поля пропорциональна объему, занимаемому полем. Разделив обе части выражения (89.5) на объем V, получим:

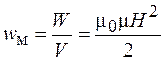. (89.6)

Здесь 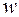– объемная плотность энергии магнитного поля, численно равная энергии поля, заключенной в единице объема.

Полученная формула аналогична выражению 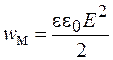для плотности энергии электрического поля.

Выражению (89.6) можно придать другой вид, используя зависимость магнитной индукции от напряженности поля (65.5):

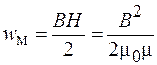. (89.7)

Если магнитное поле неоднородно, плотность энергии больше там, где больше напряженность Н и магнитная проницаемость 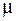. Чтобы найти энергию магнитного поля, заключенного в некотором объеме V, нужно вычислить интеграл

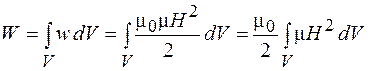. (89.8)