Закон Фарадея для электродвижущей силы индукции

Связь между 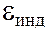и скоростью изменения магнитного потока 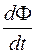можно найти с помощью закона сохранения энергии. Контур сопротивлением R находится в магнитном поле с индукцией 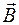(рис. 86.1). Ток I в контуре поддерживается источником ЭДС. Пусть в контуре есть подвижная часть – проводник МN. Пусть при перемещении МN в положение 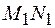за некоторое время 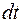поток вектора магнитной индукции через контур меняется на 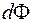. Здесь 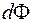– поток через площадку 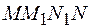. Считаем, что сопротивление R контура при этом перемещении не меняется.

За время 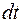источник тока совершит работу:

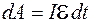. (86.1)

Эта работа затрачивается на нагревание проводников:

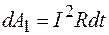(86.2)

и на перемещение проводника:

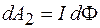. (86.3)

По закону сохранения энергии

. (86.4)

Из равенств (86.1)–(86.4) получаем:

.

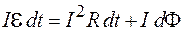Отсюда находим силу тока:

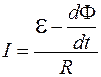. (86.5)

Если бы поток через контур не менялся ( 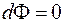), то из формулы (86.5) 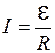– закон Ома для замкнутой цепи с ЭДС. Так как , то в цепи кроме ЭДС источника тока действует ЭДС индукции 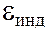, и тогда ток в цепи определится выражением

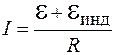. (86.6)

Сопоставив выражения (86.5) и (86.6), находим:

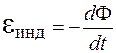. (86.7)

Выражение (86.7) – закон электромагнитной индукции (закон Фарадея). Можно показать, что закон Фарадея справедлив при любом способе изменения магнитного потока: при изменении формы контура, вращении, перемещении в неоднородном поле, изменении магнитной индукции. Знак "–" в формуле (86.7) отражает связь между знаком ЭДС индукции и знаком изменения магнитного потока. Если магнитный поток возрастает со временем 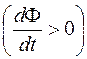, то 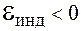, т. е. магнитное поле индукционного тока препятствует нарастанию потока; если 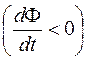, то , т. е. поле индукционного тока поддерживает ослабевающий магнитный поток.