Двух магнетиков

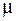На границе раздела двух сред с разными значениями относительной магнитной проницаемости линии магнитной индукции подобно линиям напряженности электрического поля изменяют направление, т. е. преломляются. Рассмотрим границу раздела двух сред с относительными магнитными проницаемостям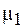и и 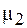(рис. 94.1). Вообразим параллелепипед с малой высотой h и с основанием 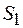, находящийся в среде с относительной магнитной проницаемостью 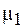, и с основанием 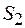– в среде с относительной магнитной проницаемостью 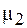. При этом 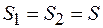. Если – нормальная составляющая вектора магнитной индукции в среде 1, а 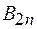– в среде 2, то поток через верхнее основание будет равен 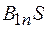, а через нижнее – (– 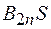). Высоту h будем считать бесконечно малой и поэтому поток через боковую поверхность можно не учитывать. Тогда поток вектора 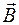через поверхность параллелепипеда

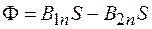. (94.1)

Но так как поток вектора 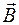через замкнутую поверхность равен нулю, то из выражения (94.1) получаем:

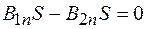
или

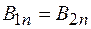. (94.2)

Равенство (94.2) показывает, что нормальная составляющая вектора магнитной индукции непрерывна. Учитывая, что 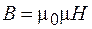, на основании формулы (95.2) находим:

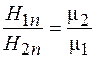. (94.3)

Из выражения (94.3) следует, что нормальные составляющие напряженности магнитного поля в разных средах различны.

Рассмотрим теперь прямоугольный контур L бесконечно малой высоты h, одна сторона которого длиной l лежит в среде 1, а другая – в среде 2 (рис. 94.2). К замкнутому контуру L применим теорему о циркуляции вектора 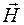(формула (71.4)): .

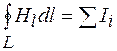Для рассматриваемого контура L

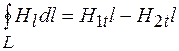. (94.4)

Если 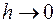, то и площадь, ограниченная контуром, стремится к нулю, а значит, стремится к нулю и сила тока, проходящего через эту площадь. Поэтому, если токов нет и на границе раздела, то

.

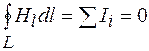Учитывая это в формуле (94.4), получаем 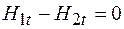или

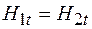. (94.5)

Выражение (94.5) показывает, что при переходе через границу раздела двух сред касательные (тангенциальные) составляющие напряженности магнитного поля не изменяются.

Подставив в равенство (94.5) 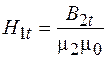и 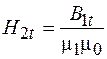, находим:

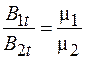. (94.6)

Из соотношения (94.6) следует, что касательные составляющие вектора магнитной индукции при переходе из одной среды в другую изменяются пропорционально относительной магнитной проницаемости.

Соотношения (94.2), (94.3), (94.5), (94.6) выполняются во всех случаях и выражают граничные условия для магнитного поля. Получим закон преломления линий вектора магнитной индукции (рис. 94.3). Из чертежа находим:

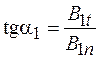; (94.7)

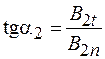, (94.8)

где 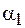– угол между линиями магнитной индукции и нормалью к поверхности раздела в среде 1; 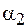– соответствующий угол в среде 2.

Разделив выражение (94.7) на выражение (94.8) и приняв во внимание формулу (94.2), получим:

.

Учитывая соотношение (94.6), найдем:

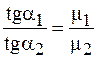. (94.9)

Выражение (94.9) – закон преломления линий магнитной индукции. В изотропных магнетиках направления векторов магнитной индукции и напряженности магнитного поля совпадают. Потому соотношение (94.9) выражает также и закон преломления линий напряженности магнитного поля.

Из формулы (94.9) следует, что линии магнитной индукции, переходя в среду с большей относительной магнитной проницаемостью, удаляются от нормали, а следовательно, сгущаются.