Вихревое электрическое поле

Электростатическое поле, т. е. поле неподвижных зарядов, является потенциальным. Для него циркуляция вектора напряженности 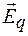равна нулю:

.

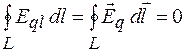Силовые линии электростатического поля не замкнуты: они начинаются на положительных зарядах и кончаются на отрицательных. Под действием электрического поля в направлении его силовых линий перемещается электрический заряд. Как известно, работа электростатического поля при перемещении заряда по замкнутому контуру равна нулю.

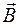Рассмотрим в переменном магнитном поле замкнутый проводящий контур L (рис. 97.1). Так как индукция магнитного поля с течением времени меняется, то будет меняться и магнитный поток Ф, пронизывающий площадь, ограниченную контуром. Но тогда по закону Фарадея в контуре возникает ЭДС индукции (86.7).

Существование ЭДС в контуре означает возникновение в нем электрического поля c напряженностью 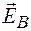. Под действием этого поля в контуре возникает перемещение свободных зарядов, т. е. электрический ток. Но так как заряды движутся вдоль силовых линий электрического поля, то одна из этих линий совпадает с контуром L, т. е. силовая линия электрического поля, возникающего в контуре, является замкнутой.

Поскольку циркуляция вектора 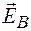и ЭДС численно равны работе перемещения единичного заряда по замкнутому контуру, можно приравнять циркуляцию вектора 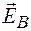и ЭДС индукции:

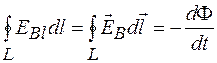. (97.1)

Из равенства (97.1) следует, что циркуляция вектора 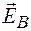не равна нулю. А это означает, что возникшее в контуре электрическое поле является вихревым, его силовые линии замкнуты.

Максвелл предположил, что изменяющееся со временем магнитное поле вызывает появление в пространстве вихревого электрического поля независимо от присутствия проводящего контура. Наличие контура лишь позволяет обнаружить по возникновении в нем индукционного тока существование электрического поля.

Выше было установлено, что поток вектора 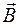через некоторую поверхность S определяется как

.

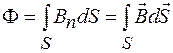Подставим это соотношение в формулу (97.1):

.

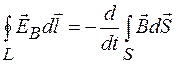Поменяв местами в правой части этого равенства операции интегрирования и дифференцирования и перейдя к частной производной по времени, получим:

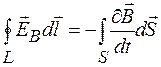. (97.2)

В равенстве (97.2) присутствует частная производная вектора 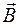по времени, потому что магнитная индукция может зависеть еще и от координат точки в пространстве.

Таким образом, электрическое поле может быть как потенциальным (полем неподвижных зарядов 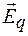), так и вихревым (полем 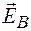, обусловленным изменяющимся со временем магнитным полем). Для напряженности суммарного электрического поля можно написать:

.

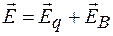И тогда для этого суммарного поля выражение (97.2) примет вид

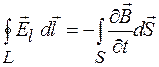, (97.3)

где L – произвольный замкнутый контур; S – произвольная поверхность, ограниченная этим контуром.

Таким образом, по гипотезе Максвелла, всюду, где есть изменяющееся со временем магнитное поле, возникает электрическое поле, в общем случае тоже переменное. Уравнение (97.3) – одно из основных уравнений электромагнитной теории Максвелла.

На использовании вихревого электрического поля основано действие циклического индукционного ускорителя электронов – бетатрона. Схематический разрез бетатрона представлен на рисунке 97.2. Здесь 1 – электромагнит; 2 – кольцевая вакуумная ускоряющая камера, внутри которой движутся электроны. Энергия частиц увеличивается за счет вихревого электрического поля, создаваемого изменяющимся магнитным потоком, пронизывающим орбиту частиц. Удержание ускоряемых электронов на равновесной круговой орбите осуществляется управляющим магнитным полем, надлежащим образом меняющимся во времени. Радиус 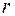мгновенной орбиты электрона, обладающего импульсом 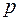, равен

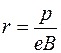, (97.4)

где 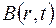– магнитная индукция поля.