На электрическое и магнитное поля
Рассмотрим применение уравнений (101.20) для некоторых частных случаев. Пусть в системе К магнитное поле отсутствует, т. е.  в любой точке. Тогда из этих уравнений для системы К' получаем:
в любой точке. Тогда из этих уравнений для системы К' получаем:
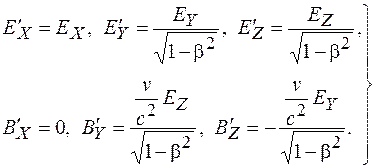 (102.1)
(102.1)
Выразив 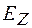 через
через  ,
, 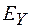 через
через  , находим, что между электрическим и магнитным полями в любой точке К' существуют соотношения:
, находим, что между электрическим и магнитным полями в любой точке К' существуют соотношения:
 . (102.2)
. (102.2)
Учитывая, что скорость системы К относительно систе- мы К' совпадает с отрицательным направлением оси O'X', соотношение (102.2) можно записать в виде
 , (102.3)
, (102.3)
где  – наблюдаемая из системы К' скорость той системы К, в которой везде
– наблюдаемая из системы К' скорость той системы К, в которой везде  .
.
Проведенные рассуждения показывают, что если в системе К наблюдается только одно электрическое поле, то в системе К' – и электрическое, и магнитное поля, связанные между собой соотношением (102.3).
Таким образом, можно прийти к выводу: если в системе К во всех точках отсутствует электрическое поле ( 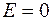 ), то в системе К' получим:
), то в системе К' получим:
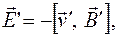 (102.4)
(102.4)
где  – скорость системы К, наблюдаемая из системы К'..
– скорость системы К, наблюдаемая из системы К'..
Следовательно, если в системе К наблюдается только одно магнитное поле, то в системе К' – и электрическое, и магнитное поля, связанные уравнением (102.4).
Таким образом, разделение электромагнитного поля на электрическое и магнитное и выделение отдельно существующих электрического и магнитного полей зависит от того, в какой системе отсчета рассматриваются поля. Обычно не существует такой системы отсчета, в которой  во всех точках, или такой системы отсчета, в каждой точке которой
во всех точках, или такой системы отсчета, в каждой точке которой 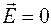 .
.
Так как в уравнениях (102.3) и (102.4) содержатся величины, измеренные в одной и той же системе отсчета (  ,
,  ,
,  ), то их удобно применять к неоднородным полям.
), то их удобно применять к неоднородным полям.
Если точечный заряд q неподвижен в системе К, то в этой системе создано только электрическое поле, а магнитное поле отсутствует. В системе К', относительно которой заряд движется со скоростью 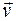 , наблюдаются и электрическое, и магнитное поля; при этом
, наблюдаются и электрическое, и магнитное поля; при этом  и оба поля перпендикулярны вектору
и оба поля перпендикулярны вектору 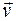 . Если скорость движения заряда велика (
. Если скорость движения заряда велика (  ), то из формулы (102.3) получаем соотношение для численных значений величин
), то из формулы (102.3) получаем соотношение для численных значений величин 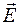 и
и 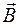 :
:  .
.
§ 103. Инвариантность уравнений Максвелла
Дата добавления: 2015-08-08; просмотров: 867;
