И электромагнитных полей
1. Инвариантность зарядов
Специальная теория относительности уходит своими историческими корнями в электромагнетизм. Г. Лоренц, исследуя электродинамику движущихся зарядов, очень близко подошел к окончательной формулировке А. Эйнштейна, великая работа которого, появившаяся в 1905 г., была озаглавлена "Об электродинамике движущихся тел". Сегодня в постулатах теории относительности и в их следствиях мы видим широкую картину, охватывающую все физические законы, а не только законы электромагнетизма. Любая полная физическая теория должна быть релятивистски инвариантной. Физическое описание событий должно быть одинаковым во всех инерциальных системах отсчета.
Имеются исчерпывающие экспериментальные доказательства того, что полный заряд системы не меняется при движении носителей заряда. Ярким подтверждением этого является полная электрическая нейтральность атомов и молекул. В атомах водорода и гелия движение одних и тех же частиц (электронов и протонов) происходит по-разному, но оба эти атома сохраняют электронейтральность. Другое доказательство связано с изучением оптических спектров изотопов одного и того же элемента. Состав ядер и характер движения протонов в ядрах изотопов различен. Сравнение спектральных линий двух изотопов не обнаруживает расхождения, которое могло бы быть приписано даже малому различию в полном заряде ядра. Это говорит о том, что электрический заряд инвариантен (независим) по отношению к разным системам отсчета.
Инвариантность заряда придает особую важность его квантованию, т. е. существованию элементарного электрического заряда. Равенство зарядов элементарных частиц справедливо не только для покоящихся друг относительно друга частиц, но и для любого состояния их относительного движения.
Инвариантность заряда означает, что величина поверхностного интеграла  в теореме Гаусса зависит только от числа и типа заряженных частиц внутри поверхности S, а не от характера их движения. Согласно постулату специальной теории относительности, если это утверждение верно для одной инерциальной системы отсчета К, то оно должно быть справедливо и для любой другой инерциальной системы
в теореме Гаусса зависит только от числа и типа заряженных частиц внутри поверхности S, а не от характера их движения. Согласно постулату специальной теории относительности, если это утверждение верно для одной инерциальной системы отсчета К, то оно должно быть справедливо и для любой другой инерциальной системы  . Тогда можно записать:
. Тогда можно записать:
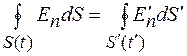 . (101.1)
. (101.1)
При этом должно выполняться условие, что в момент времени 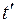 внутри поверхности
внутри поверхности 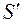 должны находиться те же заряды, что и внутри поверхности S в момент времени
должны находиться те же заряды, что и внутри поверхности S в момент времени 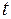 . Уравнение (101.1) формально выражает релятивистскую инвариантность заряда.
. Уравнение (101.1) формально выражает релятивистскую инвариантность заряда.
2. Преобразование электрических полей
Если заряд инвариантен относительно преобразований Лоренца, то электрическое поле должно преобразовываться определенным образом. Рассмотрим однородное поле плоского конденсатора в системах отсчета К и  , движущихся относительно друг друга со скоростью
, движущихся относительно друг друга со скоростью 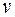 .
.
Пусть пластины конденсатора будут квадратными со стороной a, значительно большей расстояния между ними (рис. 101.1). Поверхностная плотность заряда на пластинах 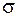 . Напряженность электрического поля в неподвижной относительно конденсатора системе К (рис. 101.2) будет равна
. Напряженность электрического поля в неподвижной относительно конденсатора системе К (рис. 101.2) будет равна
 |
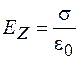 . (101.2)
. (101.2)
 Система К' движется в направлении оси OХ со скоростью
Система К' движется в направлении оси OХ со скоростью 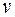 (рис. 101.3). Размер пластин вдоль оси O'X' вследствие лоренцева сокращения (19.3) уменьшается до
(рис. 101.3). Размер пластин вдоль оси O'X' вследствие лоренцева сокращения (19.3) уменьшается до 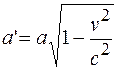 , а вдоль оси O'Y' он сохраняется. Для удобства записи введем обозначение
, а вдоль оси O'Y' он сохраняется. Для удобства записи введем обозначение 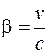 . Учитывая инвариантность заряда, для системы К' получаем:
. Учитывая инвариантность заряда, для системы К' получаем:
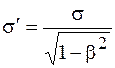 ; (101.3)
; (101.3)
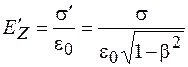 . (101.4)
. (101.4)
Из формул (101.2) и (101.4) следует:
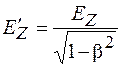 . (101.5)
. (101.5)
Равенство (101.5) показывает, что при движении в направлении, перпендикулярном вектору напряженности 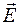 , происходит увеличение напряженности электрического поля.
, происходит увеличение напряженности электрического поля.
 Рассмотрим теперь движение плоского конденсатора в направлении, параллельном вектору
Рассмотрим теперь движение плоского конденсатора в направлении, параллельном вектору 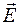 (вдоль оси ОХ на рис. 101.4). При этом размер пластин и в системе К, и в системе К' одинаков (
(вдоль оси ОХ на рис. 101.4). При этом размер пластин и в системе К, и в системе К' одинаков (  ). А это означает, что
). А это означает, что 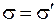 . Поэтому
. Поэтому 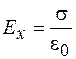 ,
, 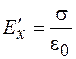 . Следовательно
. Следовательно
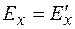 . (101.6)
. (101.6)
Выражение (101.6) показывает, что поле, параллельное направлению движения, не меняется. Соотношения (101.5) и (101.6) справедливы для любого электрического поля.
Таким образом, если в системе К неподвижные заряды создают электрическое поле напряженностью 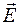 , то в системе К', движущейся со скоростью
, то в системе К', движущейся со скоростью 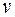 относительно системы К, будем иметь
относительно системы К, будем иметь
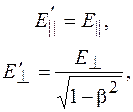 (101.7)
(101.7)
где 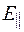 и
и 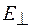 ,
, 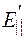 и
и 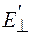 – проекции вектора
– проекции вектора 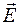 , параллельные и перпендикулярные вектору скорости
, параллельные и перпендикулярные вектору скорости 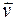 соответственно в системах К и К'.
соответственно в системах К и К'.
Если же заряды, создающие поле, движутся и в системе К, то для описания электрического поля в системе К' нужно знать два поля в системе К – электрическое и магнитное.
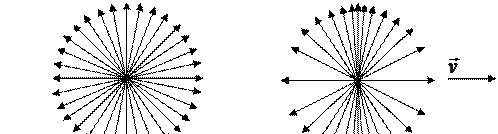 |
В качестве иллюстрации зависимости (101.7) рассмотрим электрическое поле точечного заряда. Как известно, поле неподвижного заряда имеет симметричный вид (рис. 101.5, а). Если заряд движется со скоростью, близкой к скорости света, то в направлении движения поле ослабевает, зато в перпендикулярном направлении возрастает. На рисунке 101.5, б это показано с помощью плотности линий напряженности: в направлении, перпендикулярном движению, плотность больше, а в направлении движения – меньше.
3. Релятивистское преобразование электромагнитных полей
Рассмотрим два бесконечных плоских листа, заряженных разноименно с поверхностной плотностью заряда 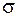 и расположенных параллельно плоскости ХОZ в системе К, относительно которой листы движутся со скоростью
и расположенных параллельно плоскости ХОZ в системе К, относительно которой листы движутся со скоростью 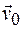 (рис. 101.6). Постоянное электрическое поле в системе К направлено вдоль оси Y и для него
(рис. 101.6). Постоянное электрическое поле в системе К направлено вдоль оси Y и для него 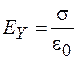 .
.
 Лист с поверхностной плотностью заряда
Лист с поверхностной плотностью заряда 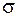 , двигаясь параллельно самому себе, создает поверхностный ток. Выделим на листе квадратную площадку со сторонойb. Сила тока, созданного этой площадкой
, двигаясь параллельно самому себе, создает поверхностный ток. Выделим на листе квадратную площадку со сторонойb. Сила тока, созданного этой площадкой 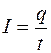 . Так как
. Так как 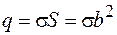 , то получаем:
, то получаем:
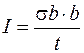 . (101.8)
. (101.8)
Величина 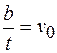 – скорость движения листа. Тогда формула (101.8) принимает вид
– скорость движения листа. Тогда формула (101.8) принимает вид
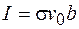 . (101.9)
. (101.9)
Сила тока  , приходящаяся на единицу длины листа, определится выражением
, приходящаяся на единицу длины листа, определится выражением
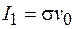 . (101.10)
. (101.10)
Поверхностный ток создает между листами магнитное поле, индукция которого 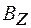 направлена вдоль оси Z. Можно доказать, что она равна
направлена вдоль оси Z. Можно доказать, что она равна  , или с учетом выражения (101.10)
, или с учетом выражения (101.10)
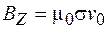 . (101.11)
. (101.11)
Рассмотрим теперь инерциальную систему К', движущуюся относительно системы К со скоростью 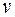 в положительном направлении оси Х (рис. 101.7). Установим, что представляют собой источники электрического и магнитного полей в системе К'. Скорость движения листов в системе К'
в положительном направлении оси Х (рис. 101.7). Установим, что представляют собой источники электрического и магнитного полей в системе К'. Скорость движения листов в системе К' 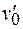 найдем по теореме сложения скоростей в теории относительности:
найдем по теореме сложения скоростей в теории относительности:

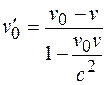 . (101.12)
. (101.12)
Сила тока в системе К' равна
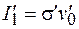 , (101.13)
, (101.13)
где 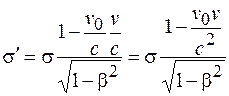 . (101.14)
. (101.14)
С учетом выражений (101.14) и (101.12) соотношение (101.13) принимает вид
 . (101.15)
. (101.15)
Во всех инерциальных системах математическая форма записи законов и уравнений физики должна быть одинаковой. Поэтому в системе К'
 и
и 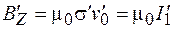 . (101.16)
. (101.16)
Эти формулы можно представить с учетом выражений (101.13) и (101.14) в виде
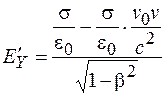 ,
,
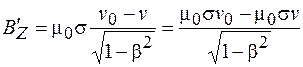 .
.
Используя соотношения (101.2) и (101.11), а также связь скорости света с электрической и магнитной постоянными 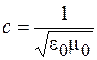 , преобразуем полученные формулы к виду
, преобразуем полученные формулы к виду
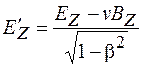 и
и 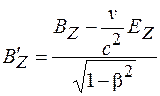 . (101.17)
. (101.17)
Если бы листы были расположены параллельно плоскости ХОY, то 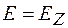 и
и  (или
(или 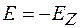 и
и 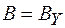 ). Это обстоятельство приводит к изменению знака в уравнениях, выражающих
). Это обстоятельство приводит к изменению знака в уравнениях, выражающих  через
через 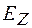 и
и 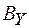 , а
, а 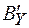 через
через 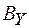 и
и 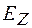 :
:
 ,
, 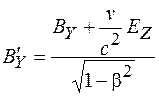 . (101.18)
. (101.18)
В направлении движения (в направлении оси Х) составляющие электрического ( 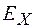 и
и 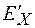 ) и магнитного (
) и магнитного ( 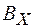 и
и 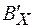 ) полей остаются неизменными при использовании преобразований Лоренца. Тогда можно записать:
) полей остаются неизменными при использовании преобразований Лоренца. Тогда можно записать:
 . (101.19)
. (101.19)
Все приведенные рассуждения справедливы для любых полей. Поэтому, объединяя вместе все соотношения для составляющих электрического и магнитного полей в разных системах отсчета, получаем:
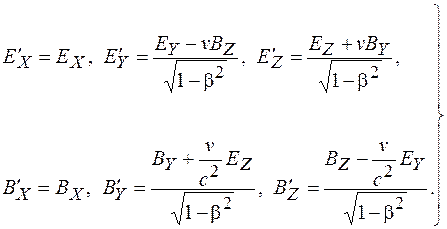 (101.20)
(101.20)
Уравнения преобразования полей симметричны в отношении векторов 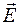 и
и 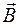 . Различия в знаках в соответствующих выражениях вытекают из правила для определения направления вектора
. Различия в знаках в соответствующих выражениях вытекают из правила для определения направления вектора 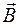 .
.
Из выражений (101.20) можно сделать вывод, что электрические и магнитные поля являются различными компонентами одного физического объекта – электромагнитного поля. Тогда величины 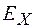 ,
, 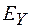 ,
, 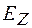 ,
, 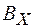 ,
, 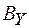 ,
, 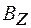 можно считать шестью компонентами этого поля. Одно и то же поле, рассматриваемое в различных инерциальных системах координат, будет представлено различными наборами значений этих компонент.
можно считать шестью компонентами этого поля. Одно и то же поле, рассматриваемое в различных инерциальных системах координат, будет представлено различными наборами значений этих компонент.
4. Взаимодействие между движущимся зарядом и другими движущимися зарядами
Магнитное взаимодействие электрических токов является в современной теории неизбежным следствием закона Кулона. Если справедливы постулаты теории относительности, если электрический заряд инвариантен и если справедлив закон Кулона, то явления, которые принято называть "магнитными", обязаны существовать. Они должны наблюдаться при электрическом взаимодействии между движущимся зарядом и другими движущимися зарядами. Это можно показать с помощью мысленного опыта.
Пусть мы имеем в системе отсчета 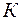 бесконечно длинную цепочку положительных зарядов, движущуюся влево со скоростью
бесконечно длинную цепочку положительных зарядов, движущуюся влево со скоростью 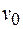 и наложенную на нее цепочку отрицательных зарядов, движущуюся с той же скоростью вправо (рис. 101.8). Заряды так многочисленны и так близко расположены друг к другу, что их дискретностью можно пренебречь. Пусть линейная плотность положительных и отрицательных зарядов в системе
и наложенную на нее цепочку отрицательных зарядов, движущуюся с той же скоростью вправо (рис. 101.8). Заряды так многочисленны и так близко расположены друг к другу, что их дискретностью можно пренебречь. Пусть линейная плотность положительных и отрицательных зарядов в системе 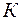 одинакова и равна
одинакова и равна 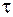 . Тогда полная
. Тогда полная  линейная плотность зарядов в системе
линейная плотность зарядов в системе 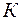 равна нулю. Следовательно, равно нулю и электрическое поле
равна нулю. Следовательно, равно нулю и электрическое поле 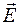 в этой системе. Здесь мы имеем аналог незаряженной проволоки, по которой протекает электрический ток. В металлической проволоке движутся только отрицательные заряды (электроны), а положительные заряды неподвижны. Мы взяли более симметричную модель, что немного упростит рассуждения. На неподвижный пробный заряд
в этой системе. Здесь мы имеем аналог незаряженной проволоки, по которой протекает электрический ток. В металлической проволоке движутся только отрицательные заряды (электроны), а положительные заряды неподвижны. Мы взяли более симметричную модель, что немного упростит рассуждения. На неподвижный пробный заряд  , находящийся от "проволоки" на некотором расстоянии
, находящийся от "проволоки" на некотором расстоянии 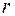 , не действуют никакие силы, потому что
, не действуют никакие силы, потому что 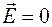 .
.
Посмотрим на ситуацию из системы отсчета, связанной с положительными зарядами. В этой системе отсчета положительные заряды покоятся, а система 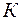 будет двигаться относительно нее. В результате лоренцева сокращения происходит уплотнение распределения зарядов в
будет двигаться относительно нее. В результате лоренцева сокращения происходит уплотнение распределения зарядов в  раз. Так как плотность зарядов в системе
раз. Так как плотность зарядов в системе 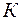 мы обозначили
мы обозначили 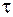 , то плотность в системе покоя положительных зарядов должна быть меньше, а именно
, то плотность в системе покоя положительных зарядов должна быть меньше, а именно  . То же самое справедливо и для линейной плотности отрицательных зарядов в их системе покоя.
. То же самое справедливо и для линейной плотности отрицательных зарядов в их системе покоя.
Пусть теперь пробный заряд  движется относительно системы
движется относительно системы 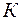 вправо со скоростью
вправо со скоростью 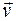 . Определим силу, действующую на него в системе
. Определим силу, действующую на него в системе 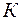 . Переходим в систему координат
. Переходим в систему координат  , движущуюся вместе с пробным зарядом
, движущуюся вместе с пробным зарядом  . В этой системе пробный заряд неподвижен, и действующая на него сила определяется исключительно электрическим полем в этой системе отсчета.
. В этой системе пробный заряд неподвижен, и действующая на него сила определяется исключительно электрическим полем в этой системе отсчета.
Откуда берется в "системе частицы" поле, которого не было в системе 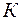 ? Дело в том, что линейные плотности зарядов, наблюдающихся в системе
? Дело в том, что линейные плотности зарядов, наблюдающихся в системе  ,
, 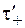 и
и 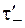 не равны друг другу. В "системе частицы" проволока оказывается заряженной. На ней имеется избыток отрицательных зарядов (рис. 101.9).
не равны друг другу. В "системе частицы" проволока оказывается заряженной. На ней имеется избыток отрицательных зарядов (рис. 101.9).
Напряженность электрического поля в системе  равна
равна
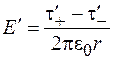 . (101.21)
. (101.21)
 Чтобы разобраться в этом, нам надо знать скорости положительных и отрицательных зарядов в системе отсчета
Чтобы разобраться в этом, нам надо знать скорости положительных и отрицательных зарядов в системе отсчета  . Очевидно, они не будут одинаковыми. Действительно, поскольку "система ча-стицы" движется вправо по отношению к системе
. Очевидно, они не будут одинаковыми. Действительно, поскольку "система ча-стицы" движется вправо по отношению к системе 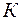 , она догоняет положительные заряды и уходит от отрицательных. Для определения
, она догоняет положительные заряды и уходит от отрицательных. Для определения 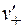 и
и  используем релятивистские формулы сложения скоростей:
используем релятивистские формулы сложения скоростей:

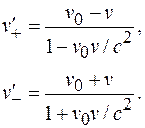 (101.22)
(101.22)
Из выражений (101.22) видно, что скорость движения отрицательных зарядов больше, чем положительных.
Два распределения зарядов испытывают лоренцево сокращение разной величины – такова разгадка проблемы. Выше было сказано, что плотность положительных зарядов в их собственной системе покоя 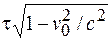 . Коэффициент, на который линейно уменьшается распределение зарядов в системе покоя частицы, равен
. Коэффициент, на который линейно уменьшается распределение зарядов в системе покоя частицы, равен 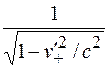 , поэтому обратная величина
, поэтому обратная величина  есть коэффициент, на который увеличивается линейная плотность зарядов по сравнению с плотностью в системе покоя положительных зарядов. Таким образом, линейная плотность положительных зарядов в си-стеме частицы должна быть равна
есть коэффициент, на который увеличивается линейная плотность зарядов по сравнению с плотностью в системе покоя положительных зарядов. Таким образом, линейная плотность положительных зарядов в си-стеме частицы должна быть равна
 . (101.23)
. (101.23)
Аналогично плотность отрицательных зарядов в системе покоя частицы равна
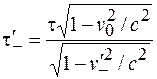 . (101.24)
. (101.24)
Полная плотность линейного заряда


Выполняя аккуратно преобразования и сокращения, в итоге мы получим:
 . (101.25)
. (101.25)
Тогда
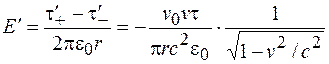 . (101.26)
. (101.26)
Следовательно, на положительный пробный заряд  действует направленная внутрь по радиусу сила:
действует направленная внутрь по радиусу сила:
 . (101.27)
. (101.27)
При измерении в системе 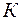 величина силы окажется другой:
величина силы окажется другой:
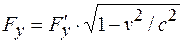 .
.
Сила, действующая на пробный заряд  , движущийся в системе
, движущийся в системе  со скоростью
со скоростью 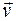 параллельно "проволоке", равна
параллельно "проволоке", равна
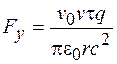 . (101.28)
. (101.28)
Это выражение можно преобразовать. Здесь  – скорость переноса положительных зарядов вправо, и такой же вклад в поле дает перенос отрицательных зарядов влево. Тогда
– скорость переноса положительных зарядов вправо, и такой же вклад в поле дает перенос отрицательных зарядов влево. Тогда  и
и
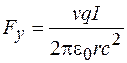 . (101.29)
. (101.29)
Примечательно, что действующая на движущийся заряд сила зависит только от силы тока и не зависит от того, как переносится заряд.
Таким образом, мы убедились, что из факта инвариантности заряда следует наличие сил между электрическими токами. Но это очень длинный и утомительный путь. Есть лучший способ: общее действие одного тока на другой может описываться полно и сжато, если ввести понятие о новом поле – магнитном.
Известно, что магнитное поле действует на движущийся заряд с силой Лоренца
 (в частном случае). (101.30)
(в частном случае). (101.30)
Сравнивая выражения (101.30) и (101.29), можно получить формулу для В:
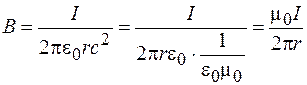 . (101.31)
. (101.31)
Мы получили формулу для магнитного поля прямого тока, исследуя только электрическое поле движущихся зарядов. Вывод немного несовершенен, но сама зависимость налицо.
Из вышесказанного ясно видно, что магнитное взаимодействие между движущимися зарядами является релятивистским эффектом. Это следовало уже из появления множителя  в уравне- нии (101.28). В мире движущихся зарядов магнетизм исчез бы, если бы скорость света оказалась бесконечно большой. Поэтому кажется странным, что магнитные силы достаточно велики, чтобы вращать якоря моторов и поднимать тяжести.
в уравне- нии (101.28). В мире движущихся зарядов магнетизм исчез бы, если бы скорость света оказалась бесконечно большой. Поэтому кажется странным, что магнитные силы достаточно велики, чтобы вращать якоря моторов и поднимать тяжести.
Заметим в заключение, что магнитные явления были бы незаметны, если бы природа не создала двух сортов зарядов, способных уничтожить силу электростатического взаимодействия.
Дата добавления: 2015-08-08; просмотров: 1457;
