Квазистационарное приближение
Квазистационарное (квазистатическое) приближение в электродинамике – это приближенное описание переменного электромагнитного поля (ЭМП), справедливое при достаточно медленных его изменениях во времени. Классификация приближений обычно основывается на безразмерных параметрах. Для электромагнитных полей в вакууме таким параметром может быть отношение
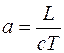 , (104.1)
, (104.1)
где 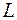 – характерный масштаб изменения поля (размер области, в которой ищется решение);
– характерный масштаб изменения поля (размер области, в которой ищется решение); 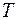 – характерный временной масштаб изменения поля.
– характерный временной масштаб изменения поля.
В соответствии с формулой (104.1) можно выделить четыре случая.
1.  – статическое приближение, статика.
– статическое приближение, статика.
А. В соответствии с этим система уравнений Максвелла для описания электростатических полей имеет вид
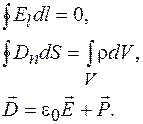 (104.2)
(104.2)
Источниками полей в электростатике служат заданные распределения плотности электрического заряда 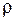 .
.
Б. Система уравнений Максвелла для описания полей в магнитостатике приобретает вид
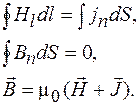 (104.3)
(104.3)
Источниками в уравнениях магнитостатики являются заданные распределения плотности электрического тока 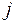 .
.
В. К статической электродинамике относят и процессы протекания постоянных токов в распределенных проводящих средах. В этом случае справедлива система уравнений (104.2), где вместо третьего уравнения записано 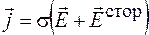 .
.
2. 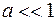 – квазистационарное (квазистатическое) приближение (квази – почти).
– квазистационарное (квазистатическое) приближение (квази – почти).
Все квазистационарные поля и процессы можно разделить на две группы. К первой принадлежат квазистационарные системы, в которых электрические и магнитные поля пространственно разнесены. Простейшим примером является колебательный контур, в котором магнитное поле сосредоточено в основном в катушке самоиндукции, а электрическое – в конденсаторе. Сюда же относятся и некоторые цепи переменного тока и переходные процессы в электрических цепях. Цепи с приближенно разнесенными электрическим и магнитным полями относят к системам с сосредоточенными параметрами.
Критерием медленности изменения поля в таких системах служит условие
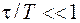 , (104.4)
, (104.4)
где 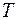 – характерное время изменения поля (например период колебаний);
– характерное время изменения поля (например период колебаний); 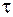 – время распространения волновых возмущений через рассматриваемую ограниченную область пространства (квазистационарную зону). Квазистационарные электрические поля определяются зарядами, а магнитные – токами, так же как в электростатике и магнитостатике и подчиняются уравнениям Максвелла (104.2), (104.3). При этом пренебрегают эффектом запаздывания, считается, что поля во всей квазистационарной зоне изменяются синхронно с источниками. Медленно изменяющимися магнитными полями наводятся электрические вихревые поля, а магнитные поля – электрическими полями. Индуцированные поля существенно изменяют характер всего физического процесса, прежде всего благодаря возникновению в проводящих контурах ЭДС индукции.
– время распространения волновых возмущений через рассматриваемую ограниченную область пространства (квазистационарную зону). Квазистационарные электрические поля определяются зарядами, а магнитные – токами, так же как в электростатике и магнитостатике и подчиняются уравнениям Максвелла (104.2), (104.3). При этом пренебрегают эффектом запаздывания, считается, что поля во всей квазистационарной зоне изменяются синхронно с источниками. Медленно изменяющимися магнитными полями наводятся электрические вихревые поля, а магнитные поля – электрическими полями. Индуцированные поля существенно изменяют характер всего физического процесса, прежде всего благодаря возникновению в проводящих контурах ЭДС индукции.
Соотношение (104.4) – условие квазистационарности тока – реально выполняется только в макроскопических системах. Квазистационарное магнитное поле качественно отличается от стационарного электрического. Это различие между электрическими и магнитными полями обусловлено явлением электромагнитной индукции, согласно которому переменное магнитное поле порождает электрическое поле, линии которого замкнуты. Поэтому квазистационарное электрическое поле не является потенциальным, оно всегда вихревое.
Вторая группа квазистационарных систем включает системы с неразделенными электрическим и магнитным полями. Примером таких объектов могут служить хорошо проводящие среды, токи проводимости в которых существенно больше токов смещения. Для таких систем характерны эффекты прижатия полей к поверхностям раздела проводник–диэлектрик (скин-эффект), наведение внешними полями вихревых токов в массивных проводниках (токи Фуко) и т. п.
Квазистационарные процессы подчиняются следующим уравнениям Максвелла:
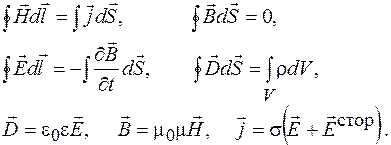 (104.5)
(104.5)
Критерием квазистационарности таких процессов является малость токов смещения по сравнению с токами проводимости:
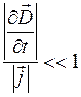 . (104.6)
. (104.6)
Для получения числовой оценки рассмотрим наиболее часто встречающийся случай, когда через среду проходит электромагнитная волна, вектор напряженности 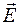 которой изменяется по гармоническому закону
которой изменяется по гармоническому закону 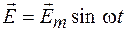 . Тогда вектор электрической индукции
. Тогда вектор электрической индукции 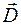 будет равен
будет равен
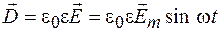 ,
,
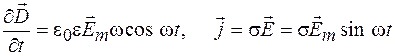 .
.
В результате для амплитудных значений получим:
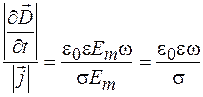 . (104.7)
. (104.7)
Здесь 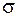 – удельная электропроводность вещества;
– удельная электропроводность вещества; 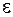 – диэлектрическая проницаемость.
– диэлектрическая проницаемость.
Таким образом, из выражения (104.7) в соответствии с выражением (104.6) следует, что условие квазистационарности электромагнитного поля можно представить в виде
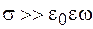 . (104.8)
. (104.8)
Отсюда следует, что условие (104.8) выполняется тем лучше, чем больше электропроводность вещества и меньше частота изменения поля. Так, например, положив для меди 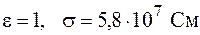 при частоте
при частоте 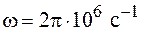 , получим:
, получим:
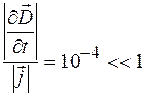 .
.
Таким образом, условие квазистационарности довольно хорошо выполняется для тонких (десятые доли миллиметра) проводников вплоть до дециметрового диапазона радиоволн. При более высоких частотах проводимость падает за счет скин-эффекта (см. формулу (105.5)) и справедливость условия (104.8) нарушается.
3. a ~1. Резонансные волновые поля описываются полной системой уравнений Максвелла. Из общего класса полей выделяются поля, возбуждаемые внутри полых волноводов либо в окрестности тонкой проволочной или щелевой антенны. При этом поля представляются дискретным набором колебаний.
4. 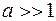 – квазиоптическое приближение.
– квазиоптическое приближение.
В заключение заметим, что квазистационарное приближение реализуется для полей любой физической природы: акустических, гравитационных и т. д. Критерием такого приближения, как и в случае электромагнитных систем, является малость параметра 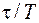 .
.
Дата добавления: 2015-08-08; просмотров: 3519;
