ПРИБЛИЖЕНИЕ СЛАБОЙ СВЯЗИ
В приближении слабой связи в качестве нулевого приближения берутся волновые функции свободного электрона, а периодическое поле кристалла рассматривается как малое возмущение. Это приближение хорошо описывает, например, электроны проводимости в металлах. В рассматриваемой модели считается, что электроны не взаимодействуют между собой, то есть образуют идеальный газ.
Рассмотрим кристалл, который для простоты будем считать имеющим форму куба со стороной L. Уравнение Шредингера (5.1) для свободного электрона 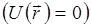 в этом случае имеет следующий вид.
в этом случае имеет следующий вид.
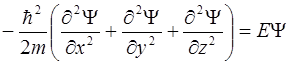 (5.4)
(5.4)
Решение уравнения (5.4) ищут в виде уравнения плоской волны:
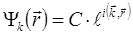 , (5.5)
, (5.5)
где 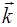 - волновой вектор электрона;
- волновой вектор электрона;
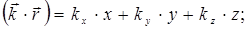 x, y, z - декартовы координаты.
x, y, z - декартовы координаты.
Отметим, что в стационарном случае зависящая от времени волновая функция содержит множитель 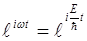 . Тогда
. Тогда  - уравнение плоской бегущей волны.
- уравнение плоской бегущей волны.
Подставив функцию (5.5) в уравнение (5.4) получим уравнение:
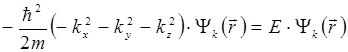 ,
,
откуда находим связь между энергией и импульсом свободного электрона
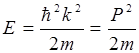 . (5.6)
. (5.6)
Константу С в выражении (5.5) найдем из условия нормировки волновой функции:
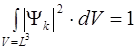 , (5.7)
, (5.7)
откуда 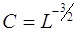
Таким образом,
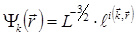 . (5.8)
. (5.8)
Поскольку кристаллическая решетка обладает свойством периодичности по координатам x,y,z, то и волновая функция (5.8) должна быть периодической по координатам с периодом h, то есть
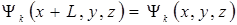 ,
,
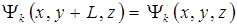 , (5.9)
, (5.9)
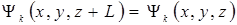
Функция (5.8) будет удовлетворять условиям (5.9) при значениях компонент волнового вектора
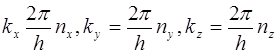 , (5.10)
, (5.10)
где nx, ny, nz - целые числа, принимающие независимо друг от друга значения 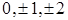 и т.д.
и т.д.
Из соотношений (5.10) следует, что компоненты волнового вектора квантуются. Подставив в выражение (5.6) 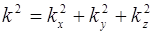 с учетом соотношений (5.10) находим собственные значения энергии
с учетом соотношений (5.10) находим собственные значения энергии
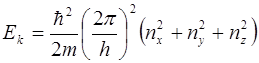 (5.11)
(5.11)
Квантовые состояния электрона в рассмотренной задаче определяются набором четырех квантовых чисел nx, ny, nz, и ms, где 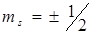 квантовое число, задающее проекцию спина на изображенное направление. Из формулы (5.11) следует, что энергия электрона зависит от суммы
квантовое число, задающее проекцию спина на изображенное направление. Из формулы (5.11) следует, что энергия электрона зависит от суммы 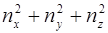 . Минимальной энергии электрона соответствуют значения
. Минимальной энергии электрона соответствуют значения 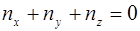 . На этом уровне можно разместить два электрона с противоположно направленными стенками (
. На этом уровне можно разместить два электрона с противоположно направленными стенками ( 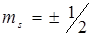 ). Третий электрон, введенный в систему, должен быть помещен с учетом принципа Паули уже на следующий уровень, для которого
). Третий электрон, введенный в систему, должен быть помещен с учетом принципа Паули уже на следующий уровень, для которого 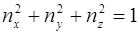 . Нетрудно убедиться, что этот уровень может быть занят двенадцатью скобами. Таким образом, уровни энергии обобществленных электронов будут вырожденными, причем краткость вырождения увеличивается с ростом энергии (для первого уровня она равна двум, для второго 12 и т.д.).
. Нетрудно убедиться, что этот уровень может быть занят двенадцатью скобами. Таким образом, уровни энергии обобществленных электронов будут вырожденными, причем краткость вырождения увеличивается с ростом энергии (для первого уровня она равна двум, для второго 12 и т.д.).
Из соотношений (5.10) следует, что интервал между соседними значениями проекций волнового вектора 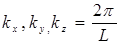 равен
равен
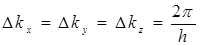 (5.12)
(5.12)
Из того, что проекции волнового вектора квантованы, следует и квантованность энергии электрона. Если линейный размер кристалла h достаточно велик 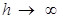 , то интервалы
, то интервалы 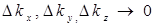 модуль волнового вектора и энергию электрона можно считать квазинепрерывными величинами. Таким образом, энергетический спектр свободного электрона хотя и состоит из дискретных точек, но они расположены так густо, что график E(k) может быть представлен в виде сплошной кривой
модуль волнового вектора и энергию электрона можно считать квазинепрерывными величинами. Таким образом, энергетический спектр свободного электрона хотя и состоит из дискретных точек, но они расположены так густо, что график E(k) может быть представлен в виде сплошной кривой
(рис. 5.5).
 Описанная модель свободных электронов объясняет ряд физических свойств металлов, однако она не может объяснить деление кристаллов на металлы, полупроводники и изоляторы.
Описанная модель свободных электронов объясняет ряд физических свойств металлов, однако она не может объяснить деление кристаллов на металлы, полупроводники и изоляторы.
Чтобы получить более полную характеристику энергетического спектра обобществленных электронов, учтем потенциальную энергию 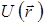 взаимодействия электрона с атомами остатками, находящимися в узлах решетки. В этом случае необходимо решать уравнение Шредингера в виде (5.1), в котором учитывается пространственная периодичность потенциального поля кристалла:
взаимодействия электрона с атомами остатками, находящимися в узлах решетки. В этом случае необходимо решать уравнение Шредингера в виде (5.1), в котором учитывается пространственная периодичность потенциального поля кристалла:
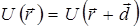 (5.13)
(5.13)
 |
Для одномерного случая зависимость
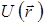 представлена на рис. 5.6.
представлена на рис. 5.6.
Как показал Блох, решения уравнения (5.1) с учетом (5.13) имеют вид
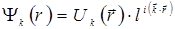 (5.14)
(5.14)
где 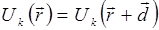 - функция координат, зависящая от волнового вектора и имеющая периодичность решетки. Отличие решения (5.14) от решения (5.5) состоит в том, что вместо константы
- функция координат, зависящая от волнового вектора и имеющая периодичность решетки. Отличие решения (5.14) от решения (5.5) состоит в том, что вместо константы 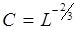 перед экспонентой стоит периодическая функция
перед экспонентой стоит периодическая функция 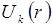 . Следовательно, функции Блоха представляют собой амплитудно-модулированные с периодом решетки плоские волны.
. Следовательно, функции Блоха представляют собой амплитудно-модулированные с периодом решетки плоские волны.
Плотность вероятности локализации электрона в различных точках выбранного направления, определяемая выражением  , так же является периодической функцией с периодом решетки (рис.5.6).
, так же является периодической функцией с периодом решетки (рис.5.6).
Решения уравнения (5.1) с учетом периодичности функции 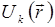 образуют наборы функций
образуют наборы функций 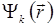 , в каждом из которых компоненты волнового вектора
, в каждом из которых компоненты волнового вектора  изменяются в переделах от
изменяются в переделах от 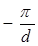 до
до 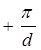 .
.
 |
Зависимость энергии электрона от волнового вектора в этом случае имеет разрывы, что указывает на существование запрещенных зон в энергетическом спектре электрона. Области изменения волнового вектора, внутри которых энергия электрона изменяется квазинепрерывно, называются зонами Бриллюэна. На границах этих зон энергия терпит разрыв. На рис. 5.7 изображены первые две зоны Бриллюэна для модели одномерного кристалла. Для трехмерной модели кристалла границами зон Бриллюэна являются многогранные поверхности в к-пространстве, вложенные одна в другую.
Таким образом, спектр возможных значений энергии электронов в кристалле представляет собой совокупность чередующихся разрешенных и запрещенных зон. Ширины зон не зависят от размера кристалла, они определяются межатомным расстоянием d и положением энергетического уровня изолированного атома (рис. 5.3).
Таким образом, несмотря на различный подход к решению задачи о поведении электронов в кристалле приближения сильной и слабой связи приводят к качественно согласующимся результатам: энергетический спектр электронов в кристалле состоит из областей разрешенных энергий (разрешенные зоны) и областей запрещенных значений энергий (запрещенные зоны).
Из того, что качественно согласующиеся результаты получены для двух предельных случаев, связанных и свободных электронов, следует их справедливость для любых промежуточных случаев.
Дата добавления: 2015-07-24; просмотров: 3464;
