ОСНОВЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ
Для описания свойств кристалла необходимо знать характер взаимодействия всех образующих его частиц (ядер и электронов). Каждая частица находится в непрерывном и достаточно сложном движении а число частиц в 1 см3 кристалла 1023-1024, поэтому описание характера взаимодействия представляет собой чрезвычайно сложную задачу. Квантовая механика позволяет сформулировать задачу о взаимодействии всех составляющих кристалл частиц в виде уравнения Шредингера, однако решить такое уравнение точно невозможно.
В современной зонной теории твердого тела используют адиабатическое и одноэлектронное приближения.
Адиабатическое приближение основано на том, что поскольку средняя кинетическая энергия ядер и электронов одного порядка, ядра можно считать практически неподвижными. Кроме того, при изменении положения ядер практически мгновенно устанавливается новое положение электронов, соответствующее новому положению ядер. Это позволяет в первом приближении рассматривать движение электронов в поле неподвижных ядер.
Многоэлектронная задача может быть сведена к одноэлектронной методом Хартри-Фока.
Идея этого метода состоит в том, что попарное взаимодействие всех электронов заменяется взаимодействием каждого электрона с усредненным полем остальных электронов. Это поле не только определяет движение данного электрона, но и само зависит от его движения (самосогласованное поле). Потенциальная энергия взаимодействия электронов с ядрами в этом методе представляется в виде суммы потенциальных энергий каждого электрона в поле всех ядер. Благодаря введенным представлениями многоэлектронная задача сводится к одноэлектронной, то есть к решению уравнения Шредингера для одного электрона:
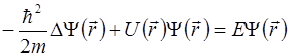, (5.1)
где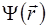 
, 
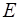и 
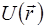- волновая функция, полная энергия и потенциальная энергия электрона в кристалле.
Уравнение (5.1) решают в приближении сильной или слабой связи. Кратко познакомимся с этими приближениями.
Дата добавления: 2015-07-24; просмотров: 852;