I. ОСНОВЫ МОЛЕКУЛЯРНОЙ СТАТИСТИКИ 2 страница
Анализ этой схемы приводит нас к выводу, что, приступая к исследованию свойств молекулярной системы в конкретных условиях, требуется прежде всего ответить на два вопроса.
1. Можно ли считать систему идеальной (неидеальной)?
2. Классическая или квантовая модель применима к описанию молекулярной системы в данных условиях?
Классических и квантовых моделей, хорошо зарекомендовавших себя при решении различных задач молекулярной физики, достаточно много. С самыми популярными из них начнем знакомиться прямо сейчас.
2.2. Идеальные статистические системы
Продвигаться от простого к сложному – один из важнейших принципов стратегии обучения. Поэтому мы начнем освоение статистического подхода на примере молекулярных систем находящихся при таких условиях, когда их можно считать идеальными.
Замкнутая система, содержащая большое число структурных элементов, называется статистической системой. Полная энергия идеальной статистической системы является аддитивной величиной:

где  – энергия структурного элемента системы,
– энергия структурного элемента системы, 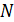 – число структурных элементов системы. Чтобы применить (2.1) к реальной макросистеме необходимо определиться с моделью материального тела. Другими словами, необходимо выяснить каковы структурные элементы системы, какие формы движения им присущи в конкретных условиях и по каким законам классической или квантовой механики можно рассчитать их одночастичные энергии
– число структурных элементов системы. Чтобы применить (2.1) к реальной макросистеме необходимо определиться с моделью материального тела. Другими словами, необходимо выяснить каковы структурные элементы системы, какие формы движения им присущи в конкретных условиях и по каким законам классической или квантовой механики можно рассчитать их одночастичные энергии  .
.
Если к структурным элементам системы применимы квантовые модели, то такую систему условимся называть квантовой системой. Соответственно, классической системой будем называть такую систему, в которой движения молекул подчиняются законам классической механики.
На схемах, приведенных ниже, даны краткие сведения об основных моделях идеальных систем и критерии их применимости. Модель идеального газа предназначена для описания поступательного движения частиц в конфигурационном пространстве. Для одноатомного газа характерно только такое движение. Обратите внимание, что использование классической модели идеального газа возможно при температурах значительно превышающих температуру вырождения 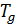 , которая пропорциональна концентрации частиц в степени 2/3 и обратно пропорциональна массе молекулы газа.
, которая пропорциональна концентрации частиц в степени 2/3 и обратно пропорциональна массе молекулы газа.
В случае многоатомного газа  необходимо учитывать и другие виды движения в зависимости от его температуры, такие как колебания атомов и вращения молекул. С этой целью в классической теории привлекаются механические модели молекул, а именно пространственные структуры материальных точек (шаров) с жесткими или упругими связями. В области применимости квантовых представлений применяются соответствующие модели осцилляторов и ротаторов с дискретными энергетическими состояниями.
необходимо учитывать и другие виды движения в зависимости от его температуры, такие как колебания атомов и вращения молекул. С этой целью в классической теории привлекаются механические модели молекул, а именно пространственные структуры материальных точек (шаров) с жесткими или упругими связями. В области применимости квантовых представлений применяются соответствующие модели осцилляторов и ротаторов с дискретными энергетическими состояниями.
Осциллятор –любая система, поведение которой обнаруживает устойчивый периодический характер.
Ротатор – вращающееся твердое тело.
Широко используемой в различных областях физики магнитных явлений, включая теорию ферромагнетизма и радиоспектроскопию, является модель системы спинов. Это сугубо квантовая модель, не имеющая классического аналога.
При решении задач вы с удивлением обнаружите, что некоторые состояния таких разных систем, как классический идеальный газ и система спинов описываются одним и тем же статистическим законом. Возможно, что восприятие вами квантовых моделей, особенно в первое время, будет сопряжено с некоторыми трудностями, имеющими скорее психологический, чем научный характер. Так получается, что мы изучаем молекулярную физику сразу после классической механики.
Не надо бояться квантовых моделей. Для понимания самого основного и существенного вполне достаточно той информации, что вы найдете на схемах 2.2.2 - 2.2.5. Не надо бояться квантовых моделей ещё и потому, что самой популярной моделью в нашем курсе будет классический идеальный газ (одноатомный и многоатомный). Скоро вы убедитесь, что эта простая модель позволяет рассмотреть очень широкий круг молекулярных явлений. Только сначала надо освоить язык теории вероятностей и молекулярной статистики.
Модели идеальных систем
Схема 2.2.2.
Молекула – материальная точка, объект классической механики. Частицы взаимодействуют по закону упругого столкновения шаров, только в момент их максимального сближения
Критерий применимости модели:
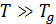 Отсутствует пространственная
конкуренция между частицами.
Энергия поступательного движения одной частицы:
Отсутствует пространственная
конкуренция между частицами.
Энергия поступательного движения одной частицы:
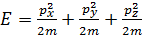 . .
|
Молекула – объект, подчиняющийся законам квантовой механики. Ее движение описывается волновой функцией.
Критерий применимости модели:
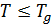 Существует пространственная
конкуренция частиц.
Энергия поступательного движения одной частицы:
Существует пространственная
конкуренция частиц.
Энергия поступательного движения одной частицы:
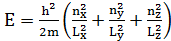 ,
где Lx, Ly, Lz – размеры сосуда, в котором находится газ; ,
где Lx, Ly, Lz – размеры сосуда, в котором находится газ; 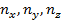 – квантовые числа. – квантовые числа. 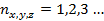 . Любое сочетание трех квантовых чисел определяет одно из разрешённых дискретных энергетических состояний молекулы. . Любое сочетание трех квантовых чисел определяет одно из разрешённых дискретных энергетических состояний молекулы.
|
| Идеальный газ |
Температура вырождения газа
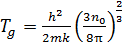 ,
здесь m – масса молекулы, ,
здесь m – масса молекулы, 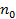 – концентрация частиц,
k=1,38·10-23Дж·К-1 – постоянная Больцмана. – концентрация частиц,
k=1,38·10-23Дж·К-1 – постоянная Больцмана.
|
| Классические модели |
| Квантовые модели |
Примеры
• Все молекулярные газы (азот, кислород, водород, гелий) имеют  значит они далеки от вырождения, и их следует рассматривать как классические системы.
• Электронный газ в хорошо проводящих металлах всегда вырожден, поскольку его значит они далеки от вырождения, и их следует рассматривать как классические системы.
• Электронный газ в хорошо проводящих металлах всегда вырожден, поскольку его 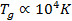 Для его описания подходит только квантовая модель идеального газа.
• Электронный газ в таких устройствах как электронно-лучевые трубки, вакуумные лампы (диоды, пентоды) соответствует модели классического идеального газа, поскольку его Для его описания подходит только квантовая модель идеального газа.
• Электронный газ в таких устройствах как электронно-лучевые трубки, вакуумные лампы (диоды, пентоды) соответствует модели классического идеального газа, поскольку его  . .
|
Схема 2.2.3.
Критерий применимости модели:
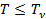 .
Энергия одномерного осциллятора: .
Энергия одномерного осциллятора:
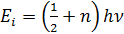 , квантовое число определяет дискретные состояния , квантовое число определяет дискретные состояния 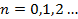 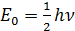 наименьшая энергия, энергия нулевых колебаний
( наименьшая энергия, энергия нулевых колебаний
( 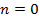 ) )

|
| Классические модели |
Критерий применимости модели:
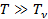 .
Энергия одномерного осциллятора: .
Энергия одномерного осциллятора:
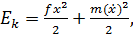 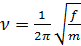 f – жесткость связи
x – смещение относительно положения равновесия.
f – жесткость связи
x – смещение относительно положения равновесия.
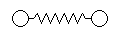 механическая модель двухатомной молекулы с упругой связью.
механическая модель двухатомной молекулы с упругой связью.
|
| Система гармонических осцилляторов |
Характеристическая температура колебаний молекул.
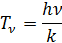
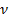 – частота колебаний осциллятора – частота колебаний осциллятора
|
| Квантовые модели |
Схема 2.2.4.
Критерий применимости модели:
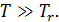 Энергия изменяется непрерывно по
степеням свободы. Энергия одномерного ротатора:
Энергия изменяется непрерывно по
степеням свободы. Энергия одномерного ротатора:
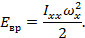
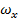 – угловая
скорость – угловая
скорость
|
Критерий применимости модели:
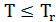 .
Энергетические уровни дискретны. Энергия одномерного ротатора: .
Энергетические уровни дискретны. Энергия одномерного ротатора:
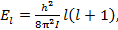 квантовое число квантовое число 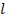 определяет момент импульса частицы L, каждому значению
определяет момент импульса частицы L, каждому значению 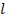 соответствует 2l+1 возможных квантовых состояний. соответствует 2l+1 возможных квантовых состояний.
|
| Система ротаторов |
Характеристическая температура вращения молекулы
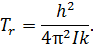
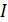 – момент инерции молекулы относительно оси вращения. – момент инерции молекулы относительно оси вращения.
|
Максимальное число вращательных степеней свободы равно трем: 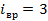 . Для линейных молекул максимальное число . Для линейных молекул максимальное число 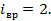
|
| Классические модели |
| Квантовые модели |
Схема 2.2.5.
Спин – специфическое квантовое свойство, собственный механический момент частицы. Спином характеризуются элементарные частицы (электроны, протоны), ядра атомов. Если заряженная частица обладает спином, то она обладает и спиновым магнитным моментом проекции которого на выделенную ось принимают 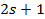 значений. Энергия частицы, обладающей магнитным моментом значений. Энергия частицы, обладающей магнитным моментом 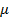 во внешнем магнитном полеВопределяется скалярным произведением: во внешнем магнитном полеВопределяется скалярным произведением: 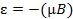 .
Квантовое число, определяющее это свойство – s, может принимать целые и полуцелые значения. Количество проекций спина на выделенное направление равно .
Квантовое число, определяющее это свойство – s, может принимать целые и полуцелые значения. Количество проекций спина на выделенное направление равно 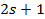 .
Пример.
Электрон обладает спином .
Пример.
Электрон обладает спином 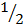 , проекция его механического момента на выделенное направление может принимать случайным образом два значения: , проекция его механического момента на выделенное направление может принимать случайным образом два значения:
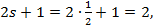 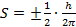 .
Проекция магнитного момента электрона также может принимать одно из двух значений .
Проекция магнитного момента электрона также может принимать одно из двух значений 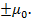 Во внешнем магнитном поле В возможны два энергетических состояния электрона: Во внешнем магнитном поле В возможны два энергетических состояния электрона:
|
| Система спинов |
| Квантовая модель |
2.3. Элементарные сведения из теории вероятностей
Приведем самые основные и необходимые нам для дальнейшего обсуждения темы определения, аксиомы и теоремы теории вероятностей. Для более обстоятельного ознакомления с ними рекомендуем [11,14] и, конечно, учебник по теории вероятностей [4]. Достаточно подробно с рассмотрением примеров этот учебный материал представлен в наших методических указаниях к семинарским занятиям. Поэтому позволим себе прибегнуть к краткому стилю изложения этой темы.
Случайные события
Случайное событие –событие, которое при осуществлении некоторого комплекса условий может либо произойти, либо не произойти. Примечание: осуществление некоторого комплекса условий в теории вероятности называется испытанием.
Суммой А+В двух событий А и В называют событие, состоящее в появлении либо события А, либо события В, либо обоих этих событий. Суммой нескольких событийназывают событие, которое состоит в появлении хотя бы одного из этих событий.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Произведением нескольких событийназывают событие, состоящее в совместном появлении всех этих событий.
События независимы, если вероятность наступления одного из них не зависит от того, наступило или не наступило другое событие.
События являются взаимно исключающими или несовместными, если вероятность наступления одного события исключает наступление другого.
Совокупность взаимно исключающих событий (попарно несовместно событий) образует полную группу, если каждый исход испытаний принадлежит ей.
Событие 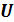 называется достоверным, если оно должно наступить при каждом испытании.
называется достоверным, если оно должно наступить при каждом испытании.
Событие 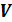 называется невозможным, если оно не происходит ни при каком испытании.
называется невозможным, если оно не происходит ни при каком испытании.
Определения вероятности событий
Вероятность случайного события есть количественная мера ожидаемой возможности его появления.
Аксиоматическое определение вероятности. Каждому событию А соответствует неотрицательное действительное число 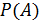 . Это число называется вероятностью события
. Это число называется вероятностью события 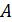 . Классическое определение вероятности.Вероятностью события
. Классическое определение вероятности.Вероятностью события 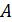 называют отношение числаблагоприятствующих этому событию исходов
называют отношение числаблагоприятствующих этому событию исходов 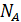 к общему числу всех равновозможных несовместных исходов
к общему числу всех равновозможных несовместных исходов 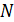 , образующих полную группу,
, образующих полную группу,

Согласно (2.2 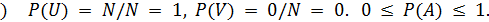
Требование равно возможности всех исходов испытаний является очень сильным. Если a priori нет способов обоснования этого положения, то следует воспользоваться другим (статистическим) определением вероятности.
Статистическое или частотное определение вероятности.
Вероятностью случайного события 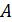 называется предел отношения числа испытаний
называется предел отношения числа испытаний 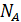 , в которых событие
, в которых событие 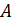 произошло, к общему числу испытаний
произошло, к общему числу испытаний 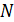 , при условии
, при условии 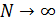

Теоремы теории вероятностей
Теорема сложения вероятностей взаимно исключающих событий. Вероятность суммы взаимно исключающих событий равна сумме вероятностей этих событий
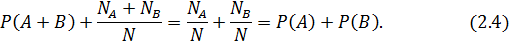
Теорема умножения вероятностей независимых событий. Вероятность произведения двух независимых событий равна произведению этих событий

Условие нормировки вероятности
Рассмотрим совокупность взаимно исключающих событий, образующих полную группу. Согласно теореме сложения вероятностей взаимно исключающих событий:
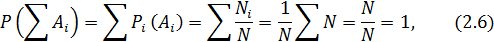
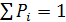 – условие нормировки вероятности.
– условие нормировки вероятности.
Состояния физической системы всегда однозначны, т.е. образуют полную совокупность событий. Условие нормировки для вероятности состояния физической системы отражает факт: если физическая система существует, то она находится в одном из доступных ей состояний.
Случайная величина
Случайной величиной называется величина, которая в результате испытаний примет одно из возможных (допустимых) значений, наперед неизвестное и зависящее от случайных причин.
Примечание. В молекулярных системах микроскопические параметры, такие как скорости, импульсы, энергии, отдельных частиц являются случайными частицами.
Дискретной называют случайную величину, которая принимает отдельные изолированные возможные значения с определенной вероятностью.
Дискретную величину можно задавать в табличной форме 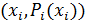 или графически в форме гистограммы.
или графически в форме гистограммы.
Непрерывной называется случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Плотность вероятности
Если состояние системы характеризуется случайной величиной  , принимающей любые значения от
, принимающей любые значения от 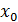 до
до 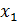 , то определение вероятности (2.1) лишено смысла, поскольку множество значений
, то определение вероятности (2.1) лишено смысла, поскольку множество значений  не является счётным. В этом случае вероятность определяется в дифференциальной форме:
не является счётным. В этом случае вероятность определяется в дифференциальной форме:

Утверждается, что для достаточно малого интервала изменений 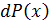 пропорциональна величине достаточно много интервала измерений переменной
пропорциональна величине достаточно много интервала измерений переменной 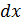 , а коэффициент пропорциональности
, а коэффициент пропорциональности 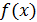 не зависит от величины этого интервала и называется плотностью вероятности
не зависит от величины этого интервала и называется плотностью вероятности

Знание плотности вероятности позволяет найти вероятность для любой области, в которой определена плотность.
Условие нормировки для плотности вероятности записывается следующим образом
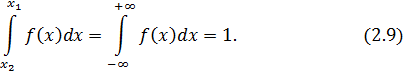
Важными числовыми характеристиками случайной величины x являются ее среднее значение 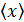 и дисперсия
и дисперсия 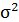 . Определения этих параметров приведены на схемах 2.3.1 и 2.3.2.
. Определения этих параметров приведены на схемах 2.3.1 и 2.3.2.
Схема 2.3.1.
| Процедура усреднения случайных величин |
| Непрерывная величина |
| Дискретная величина |
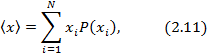 суммирование по всем доступным значениям параметра x.
суммирование по всем доступным значениям параметра x.
|
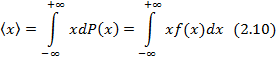 где x – принимает значения в интервале (-∞,+∞);
f(x) – плотность вероятности
где x – принимает значения в интервале (-∞,+∞);
f(x) – плотность вероятности
|
Схема 2.3.2.
| Флуктуация – отклонение случайной величины от ее среднего значения. |
Абсолютная мера флуктуации – дисперсия:
 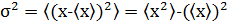 , (2.12) , (2.12)
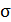 – стандартное (среднеквадратичное) отклонение.
Относительная мера флуктуации: – стандартное (среднеквадратичное) отклонение.
Относительная мера флуктуации:
 – относительное стандартное отклонение. (2.13) – относительное стандартное отклонение. (2.13)
|
2.4. Основные понятия молекулярной статистики
Состояния статистической системы подразделяют на макроскопические и микроскопические. Макроскопическим состояниям системы называется ее равновесное состояние, характеризующееся макроскопическими параметрами (см. 1.5).
Макроскопическое состояние газа характеризуется тремя параметрами 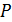 ,
,  и
и 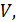 которые в стационарном состоянии постоянны.
которые в стационарном состоянии постоянны.
Микроскопическое состояние системы – это ее мгновенное состояние. Оно определяется набором параметров, характеризующих все частицы в системе.
Для классической системы микросостояние задается набором координат и импульсов, для квантовой системы – набором квантовых чисел 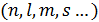 . Каждое макроскопическое состояние системы осуществляется посредством громадного множества ее микроскопических состояний.
. Каждое макроскопическое состояние системы осуществляется посредством громадного множества ее микроскопических состояний.
Другими словами, находясь в одном и том же макросостоянии, система беспрерывно меняет свои микросостояния. Для квантовых систем осуществляется переход из одного дискретного состояния в другое. В случае классических моделей возникает проблема различия микросостояний, поскольку координаты и скорости меняются непрерывно. Эта трудность была преодолена путем разбиения конфигурационного пространства и пространства импульсов на ячейки. Объем ячейки в конфигурационном пространстве равен  , где
, где 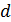 – характерный диаметр молекулы. Объем ячейки в пространстве импульсов возможно определить из квантово-механических представлений:
– характерный диаметр молекулы. Объем ячейки в пространстве импульсов возможно определить из квантово-механических представлений:
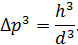
После разбиения пространства на ячейки была получена система, в которой смена состояний происходит дискретным образом, поэтому количество состояний в такой системе можно подсчитать. Число доступных системе микросостояний очень велико, поэтому для определения вероятности микроскопического состояния используется аналог частотного определения вероятности.
Вероятность микроскопического состояния.
Статистический ансамбль
Нахождение вероятности микроскопического состояния согласно (2.3) предполагает очень большое 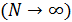 число испытаний в системе, находящейся в неизменных условиях. Поскольку многократное проведение испытаний для молекулярной системы даже как мысленный эксперимент зачастую затруднено, то в молекулярной физике подобная процедура заменяется одновременной фиксацией интересующего микроскопического состояния в очень большом множестве совершенно одинаковых систем, называемых статистическим ансамблем.
число испытаний в системе, находящейся в неизменных условиях. Поскольку многократное проведение испытаний для молекулярной системы даже как мысленный эксперимент зачастую затруднено, то в молекулярной физике подобная процедура заменяется одновременной фиксацией интересующего микроскопического состояния в очень большом множестве совершенно одинаковых систем, называемых статистическим ансамблем.
Итак, статистическим ансамблем называется большая совокупность статистических систем. Метод ансамблей введен в молекулярную физику Гиббсом.
Статистический ансамбль, который необходим для наших целей, называется микроканоническим. Микроканонический ансамбль состоит из одинаковых изолированных систем с одинаковой энергией.
В статистике используются и другие ансамбли. Например, при изучении распределения Максвелла будет актуальным канонический ансамбль систем. Канонический ансамбль представляет совокупность незамкнутых систем, имеющих возможность обмениваться энергией только между собой. Их можно рассматривать как подсистемы изолированной системы, принадлежащей микроканоническому ансамблю.
Вернемся к определению вероятности микросостояния. Для простоты рассмотрим вероятность того, что определенная молекула «с номером на спине» находится в j-ой ячейке конфигурационного пространства. Представим микроканонический ансамбль, состоящий из 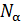 статистических систем. Число ячеек в каждой системе ансамбля равно
статистических систем. Число ячеек в каждой системе ансамбля равно 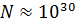 . Предполагается, что
. Предполагается, что 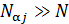 . Вследствие этого можно считать, что число
. Вследствие этого можно считать, что число 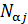 систем ансамбля, в которых выделенная частица находится в j-ой ячейке достаточно велико. Тогда в соответствии с (2.3) вероятность интересующего нас состояния
систем ансамбля, в которых выделенная частица находится в j-ой ячейке достаточно велико. Тогда в соответствии с (2.3) вероятность интересующего нас состояния

Определения вероятности (2.3) и (2.14) совершенно эквивалентны. При решении задач следует выбирать наиболее удобное из них для конкретных условий.
Статистические постулаты
Молекулярная статистика как научная теория опирается на два основополагающих допущения, не имеющих в настоящее время доказательств, и поэтому называемых постулатами. Несмотря на это все последующие положения, законы, следствия и выводы теории имеют строгие логические доказательства и экспериментальные подтверждения.
Постулаты имеют свои исторически сложившиеся названия. Первый кратко именуют постулатом равновероятности. Второй постулат называют эргодической гипотезой.
Прежде всего, дадим развернутые (двухчастные) формулировки этих постулатов (см. схему 2.4.1), а затем прокомментируем их содержания.
Комментарий к постулату равновероятности
Как можно экспериментально установить, что система находится в равновесии? Для этого надо убедиться в том, что все наблюдаемые макроскопические параметры системы не зависят от времени. Рассмотрим микроканонический ансамбль систем.
Дата добавления: 2015-08-11; просмотров: 2601;
