I. ОСНОВЫ МОЛЕКУЛЯРНОЙ СТАТИСТИКИ 7 страница

где 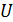 – падение напряжения на активном сопротивлении
– падение напряжения на активном сопротивлении 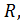
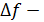 полоса частот пропускающего устройства.
полоса частот пропускающего устройства.
В 30-е годы двадцатого века был сформулирован броуновский критерий точности физических измерений, который накладывает ограничение на максимально допустимую точность измерения приборов.
При любом однократном измерении отклика 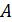 , т.е. реакции прибора на внешнее воздействие, относительная погрешность
, т.е. реакции прибора на внешнее воздействие, относительная погрешность  не будет меньше, чем величина
не будет меньше, чем величина
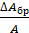 - броуновский стандарт
- броуновский стандарт
Формула для броуновского критерия точности имеет вид

Для рассмотренных выше примеров:

Для снижения погрешности измерений существует три способа:
• Многократное измерение, т.е. накопление сигнала.
Уменьшение броуновского стандарта обратно пропорционально 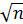 , где
, где 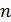 – число опытов, в свою очередь
– число опытов, в свою очередь  где
где  – время измерений. Например: если
– время измерений. Например: если 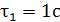 , то при увеличении времени измерений до
, то при увеличении времени измерений до 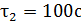 броуновский стандарт уменьшается в 10 раз (
броуновский стандарт уменьшается в 10 раз ( 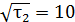 ).
).
• Уменьшение полосы частот пропускающего устройства (узкополосная измерительная схема).
• Снижение температуры  , в результате чего уменьшаются абсолютные значения самих флуктуаций.
, в результате чего уменьшаются абсолютные значения самих флуктуаций.
Во всех рассмотренных случаях (поступательное и вращательное броуновское движение, найквистовский шум) дисперсии случайных величин пропорциональны  . Это универсальное свойство проявляется в самых различных физических явлениях. Поэтому температуру можно рассматривать как меру флуктуаций случайных величин.
. Это универсальное свойство проявляется в самых различных физических явлениях. Поэтому температуру можно рассматривать как меру флуктуаций случайных величин.
7.5. Классическая теория теплоёмкости многоатомных газов. Область её применимости
Последовательное рассмотрение такой важной характеристики макросистемы как теплоёмкость нас ждёт в ближайшем будущем при изучении основ термодинамики. Забегая вперёд, отметим, что теплоёмкость зависит от процесса, который совершает система. Наиболее широкое применение, как в теории, так и на практике имеют молярные теплоёмкости для двух процессов: при постоянном объёме и при постоянном давлении 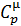 . Между собой они связаны соотношением, которое называется уравнением Майера:
. Между собой они связаны соотношением, которое называется уравнением Майера:

Получим выражения для 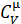 и
и 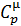 через статистические степени свободы. Будем исходить из определения молярной теплоёмкости при постоянном объёме
через статистические степени свободы. Будем исходить из определения молярной теплоёмкости при постоянном объёме

Для её вычисления внутреннюю энергию моля идеального газа запишем через статистические степени свободы согласно (7.3)
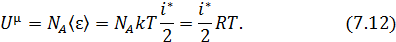
Возьмём производную от (7.12) по температуре, это и будет 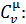

Выражение для 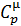 получим из уравнения (7.10).
получим из уравнения (7.10).
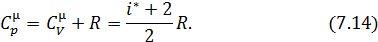
Как видно из полученных формул (7.13) и (7.14), 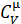 - постоянная величина, однако число
- постоянная величина, однако число 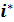 может принимать разные значения в зависимости от того, какая механическая модель молекулы оказывается адекватной в данной области температур. В рамках самой классической теории предсказать значение
может принимать разные значения в зависимости от того, какая механическая модель молекулы оказывается адекватной в данной области температур. В рамках самой классической теории предсказать значение  , т.е. установить критерий применимости модели невозможно. Анализ экспериментально измеренных теплоёмкостей газов в широком диапазоне температур свидетельствует, что существуют области, где формулы (7.13) и (7.14) вовсе неприменимы. Недостаточность классической теории теплоёмкостей, обозначенные трудности были преодолены после построения теории на квантовой основе.
, т.е. установить критерий применимости модели невозможно. Анализ экспериментально измеренных теплоёмкостей газов в широком диапазоне температур свидетельствует, что существуют области, где формулы (7.13) и (7.14) вовсе неприменимы. Недостаточность классической теории теплоёмкостей, обозначенные трудности были преодолены после построения теории на квантовой основе.
В качестве примера рассмотрим экспериментально наблюдающуюся температурную зависимость 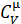 для молекулярного водорода (Рис. 7.2).
для молекулярного водорода (Рис. 7.2).
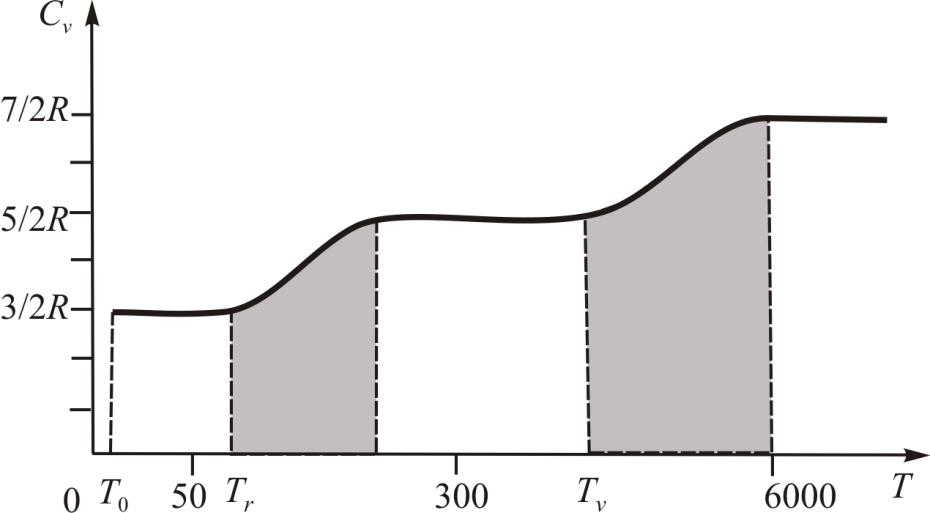
Рис. 7.2.
Из графика видно, что при низкой температуре молекула водорода ведёт себя как точечная частица, для которой характерны только поступательные степени свободы  ). При достижении температуры
). При достижении температуры 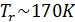 начинают «включаться» вращательные степени свободы, а при
начинают «включаться» вращательные степени свободы, а при 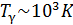 – колебательные. Области значений
– колебательные. Области значений  , где
, где 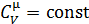 растёт с увеличением температуры – области применимости квантовых моделей материальных тел. Расчёт характеристических температур является основой для выделения областей применимости различных моделей. Отметим, что температура
растёт с увеличением температуры – области применимости квантовых моделей материальных тел. Расчёт характеристических температур является основой для выделения областей применимости различных моделей. Отметим, что температура 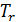 для всех двухатомных газов значительно ниже
для всех двухатомных газов значительно ниже 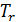 водорода. Поэтому для двухатомных молекул в широком диапазоне температур, от нескольких кельвин до тысячи,
водорода. Поэтому для двухатомных молекул в широком диапазоне температур, от нескольких кельвин до тысячи, 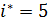 .
.
Для трехатомных и более сложных молекул газа 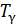 всегда меньше 273
всегда меньше 273 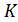 , поэтому колебательные степени свободы у таких молекул «включены» во всём диапазоне положительных температур по шкале Цельсия.
, поэтому колебательные степени свободы у таких молекул «включены» во всём диапазоне положительных температур по шкале Цельсия.
7.6. Классическая теория теплоёмкости твёрдых тел.
Закон Дюлонга – Пти
Теория теплоёмкости кристаллов основана на модели идеального твёрдого тела. В этой модели твёрдое тело (кристалл) рассматривают, как систему 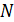 независимых друг от друга атомов, которые совершают гармонические колебания около положений равновесия, других движений нет.
независимых друг от друга атомов, которые совершают гармонические колебания около положений равновесия, других движений нет.
Каждый атом имеет три колебательные степени свободы. На одну степень свободы приходится в среднем энергия kT: kT/2 в виде кинетической, kT/2 – в виде потенциальной энергии.
Согласно (7.4) для одного моля одинаковых атомов
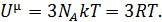
В твёрдых телах уравнение Майера (7.10) не выполняется. Пренебрегая тепловым расширением кристаллов можно записать:
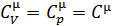 .
.
Используя (7.11) получим выражение, называемое закономДюлонга-Пти:

Молярная теплоёмкость всех химически простых твёрдых тел одинакова и равна 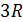 .
.
Этот закон хорошо выполняется только при сравнительно высоких температурах. Опыт показывает, что при 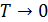 теплоёмкость кристалла убывает стремясь к нулю по закону
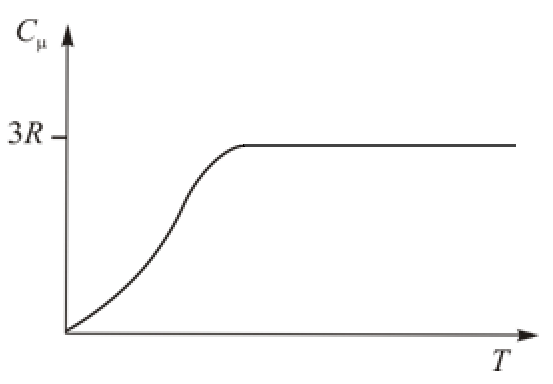
теплоёмкость кристалла убывает стремясь к нулю по закону 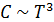 (см. рис. 7.3), что не находит объяснения в классической теории.
(см. рис. 7.3), что не находит объяснения в классической теории.
Если кристалл представляет соединение разных атомов, то число колебательных степеней свободы следует умножить на число атомов согласно его химической формуле. Например, для кристалла 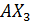 число атомов равно 4, следовательно,
число атомов равно 4, следовательно, 
| Рис. 7.3. |
7.7. Применение квантовых моделей в теории теплоёмкости твёрдых тел
В рамках классической теории оказалось невозможным объяснить зависимость теплоёмкости твёрдых тел от температуры. Для решения этого вопроса А.Эйнштейн (1907г.) предложил использовать простейшую квантовую модель твёрдого тела.
Модель Эйнштейна
• Моделью является кристалл, состоящий из 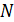 атомов, каждый из которых является квантовым гармоническим осциллятором. Колебания атомов происходят независимо друг от друга с одинаковой частотой
атомов, каждый из которых является квантовым гармоническим осциллятором. Колебания атомов происходят независимо друг от друга с одинаковой частотой 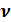 . Энергия квантового гармонического осциллятора дискретна:
. Энергия квантового гармонического осциллятора дискретна:
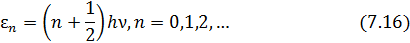
• Среднее значение 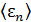 находится с помощью распределения Гиббса.
находится с помощью распределения Гиббса.

• Для молярной теплоёмкости кристаллической решётки получим выражение, называемое формулой Эйнштейна
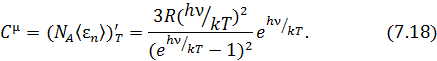
При высоких температурах 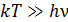 формула Эйнштейна переходит в выражение (7.15). При низких температурах (
формула Эйнштейна переходит в выражение (7.15). При низких температурах ( 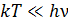 ) она приобретает вид
) она приобретает вид
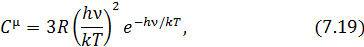
если 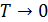 , то и
, то и 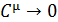 . В целом, формула Эйнштейна передаёт характер зависимости теплоёмкости от температуры, согласующейся с результатами опыта (Рис. 7.3). Вместе с тем согласие теории с экспериментальными данными наблюдается только в качественном отношении. В частности, стремление теплоёмкости к нулю при низких температурах, следуя (7.19) идёт по экспоненте, а опыт как уже упоминалось, даёт
. В целом, формула Эйнштейна передаёт характер зависимости теплоёмкости от температуры, согласующейся с результатами опыта (Рис. 7.3). Вместе с тем согласие теории с экспериментальными данными наблюдается только в качественном отношении. В частности, стремление теплоёмкости к нулю при низких температурах, следуя (7.19) идёт по экспоненте, а опыт как уже упоминалось, даёт 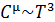 . Расхождения связаны не с существом квантовой теории, а с избыточной упрощённостью модели твёрдого тела. Сам Эйнштейн это осознавал и представлял в каком направлении должно идти развитие модели материального тела.
. Расхождения связаны не с существом квантовой теории, а с избыточной упрощённостью модели твёрдого тела. Сам Эйнштейн это осознавал и представлял в каком направлении должно идти развитие модели материального тела.
В твёрдом теле нельзя рассматривать атомы как независимые, необходимо принять во внимание их взаимодействия. Это было осуществлено в модели П. Дебая (1912г.).
Модель Дебая
Кристаллическая решётка в этой модели рассматривается как связанная система взаимодействующих атомов. Колебания такой системы – результат наложения множества гармонических колебаний с различными частотами. Задача, таким образом, сводится к нахождению спектра частот твердого тела. В общем случае это сделать очень трудно. Если же рассматривать область низких температур, то в этом диапазоне основной вклад в теплоемкость вносит низкочастотный спектр колебаний решетки, который может быть рассчитан достаточно точно.
Теория Дебая дает хорошее согласие зависимости 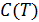 для химически простых тел с экспериментом при низких температурах, демонстрируя тем самым эвристическую силу квантового подхода.
для химически простых тел с экспериментом при низких температурах, демонстрируя тем самым эвристическую силу квантового подхода.
Мы ограничились кратким изложением теории Эйнштейна и общей характеристикой теории Дебая. Подробно эти вопросы изучаются в курсе физики твёрдого тела.
Завершая обсуждение основ статистического подхода в молекулярной физике, отметим, что в дальнейшем будем неоднократно обращаться к изученному материалу при рассмотрении разнообразных явлений в макросистемах.
Контрольные вопросы
1. Сформулируйте теорему о равнораспределении энергии. Какой факт лежит в основе её доказательства?
2. Как подсчитывается число статистических степеней свободы для многоатомных газов? С какой целью это делается?
3. Что называется броуновским движением? Какова его сущность?
4. В каких областях применяется теория броуновского движения? Кто ее создатель?
5. Каким параметром характеризуется поступательное броуновское движение? Запишите и проанализируйте формулу для него.
6. Каким параметром характеризуется вращательное броуновское движение? Запишите и проанализируйте формулу для него.
7. Сформулируйте броуновский критерий точности физических измерений. Для каких приборов он актуален?
8. Какими способами можно уменьшить погрешность измерений?
9. Как определяются молярные теплоемкости 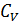 и
и 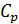 многоатомных газов в классической теории? Какова область применимости этой теории?
многоатомных газов в классической теории? Какова область применимости этой теории?
10. Как определяется молярная теплоемкость кристаллов в классической теории? Какова область применимости этой теории? Сформулируйте закон Дюлонга-Пти.
11. На основе каких предположений Эйнштейн получил формулу для теплоемкости твердого тела? Насколько хорошо теоретическая зависимость 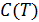 согласуется с экспериментальными данными?
согласуется с экспериментальными данными?
12. В чем отличие моделей твердого тела Эйнштейна и Дебая в квантовой теории теплоемкости?
II. ОСНОВЫ ТЕРМОДИНАМИКИ
ЛЕКЦИЯ 8
ТЕРМОДИНАМИЧЕСКИЙ ПОДХОД К ОПИСАНИЮ МОЛЕКУЛЯРНЫХ ЯВЛЕНИЙ
Дата добавления: 2015-08-11; просмотров: 2261;
