I. ОСНОВЫ МОЛЕКУЛЯРНОЙ СТАТИСТИКИ 5 страница
Вывод уравнения
• Изобразим рассматриваемую систему на схематическом рисунке
(рис. 5.1):
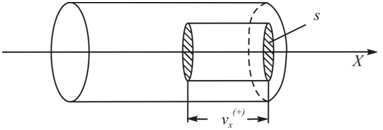
Рис. 5.1.
Обозначим направление перпендикулярное стенке сосуда как ось X, тогда вклад в давление будут вносить только «иксовые» составляющие импульсов молекул, ударяющихся о стенку. Мысленно выделим цилиндр (он показан на рис. 5.1) объёмом 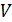 , у которого площадь основания S=1м2, а длина равна составляющей скорости
, у которого площадь основания S=1м2, а длина равна составляющей скорости 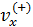 . Индекс (+) обозначает направление вдоль оси
. Индекс (+) обозначает направление вдоль оси 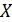 к стенке. Длина цилиндра такова, что только те молекулы, которые находятся внутри цилиндра, успеют за 1 секунду достигнуть стенки сосуда и столкнуться с ней.
к стенке. Длина цилиндра такова, что только те молекулы, которые находятся внутри цилиндра, успеют за 1 секунду достигнуть стенки сосуда и столкнуться с ней.
• Импульс, передаваемый одной молекулой сосуда при столкновении с ней равен 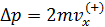 .
.
• Обозначим 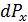 вклад в давление, который даёт группа молекул, или «команда», с некоторой фиксированной скоростью, точнее со скоростями в интервале (
вклад в давление, который даёт группа молекул, или «команда», с некоторой фиксированной скоростью, точнее со скоростями в интервале ( 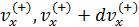 ), тогда
), тогда 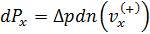 ,
,
где 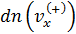 - число молекул со скоростями
- число молекул со скоростями 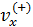 в выделённом объёме цилиндра (рис. 5.1).
в выделённом объёме цилиндра (рис. 5.1).
• 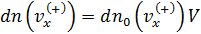 , где –
, где – 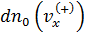 концентрация частиц, обладающих скоростями в интервале (
концентрация частиц, обладающих скоростями в интервале ( 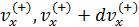 );
);
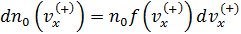 ,
,
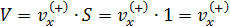 ,
,
здесь 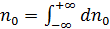 – равновесная концентрация молекул в объёме V,
– равновесная концентрация молекул в объёме V, 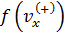 – одномерная плотность вероятности распределения Максвелла.
– одномерная плотность вероятности распределения Максвелла.
• Таким образом,
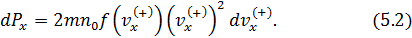
• Полученное уравнение (5.2) интегрируем по области значений 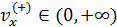 , поскольку, летящие в отрицательном направлении молекулы
, поскольку, летящие в отрицательном направлении молекулы 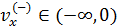 не сталкиваются с данной стенкой сосуда, следовательно, не вносят вклад в давление:
не сталкиваются с данной стенкой сосуда, следовательно, не вносят вклад в давление:
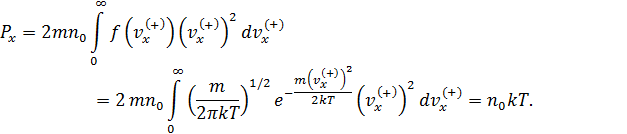
Ответ: 
Подобные расчёты для компонент давления 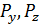 , дадут такой же результат. Как и следовало ожидать, в изотропной среде давление газа изотропно. Это утверждение известно как закон Паскаля
, дадут такой же результат. Как и следовало ожидать, в изотропной среде давление газа изотропно. Это утверждение известно как закон Паскаля

В заключение обсудим вопрос о давлении, создаваемом смесью различных в химическом отношении газов. Отдельные компоненты смеси идеальных газов можно считать независимыми, поэтому каждая компонента создаёт давление равное (5.3). Полное давление смеси газа равно сумме давлений компонент или сумме парциальных давлений 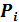
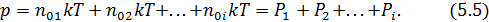
Таким образом, мы сформулировали закон Дальтона.
5.2. Основное уравнение молекулярно-кинетической теории. Газовые законы
Запишем выражение для температуры через среднюю кинетическую энергию движения молекул согласно (4.22)
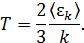
Подставив эту формулу в (5.3), получим основное уравнение молекулярной кинетической теории идеальных газов (основное уравнение МКТ)

В (5.6) и далее для обозначения давления используем строчную букву 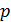 .
.
Уравнение (5.6) устанавливает простую связь между макроскопическим параметром 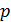 и микроскопическим параметром
и микроскопическим параметром 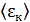 .
.
Многочисленные эмпирические законы идеальных газов были получены раньше, чем основное уравнение МКТ. В то же время, они являются естественными следствиями(5.3) и легко выводятся из него. Давайте убедимся в этом.
Подставим выражение для равновесной концентрации 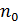 через полное число частиц
через полное число частиц 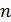 в (5.3), тогда получим
в (5.3), тогда получим

или
Сделаем замену 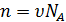 и (5.7) примет вид
и (5.7) примет вид

Произведение двух констант дает новую константу: 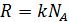 , где
, где 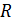 – универсальная газовая постоянная. Её значение в СИ равно 8,31 Дж / моль∙К. Газовую постоянную ввел в научный обиход наш знаменитый соотечественник Д.И. Менделеев.
– универсальная газовая постоянная. Её значение в СИ равно 8,31 Дж / моль∙К. Газовую постоянную ввел в научный обиход наш знаменитый соотечественник Д.И. Менделеев.
Перепишем (5.8) окончательно

или

Уравнения (5.7), (5.9) и (5.10) представляют разные варианты записи уравнения состояния идеального газа. Если уравнение состояния содержит постоянную 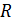 , то его называют уравнением Клапейрона-Менделеева.
, то его называют уравнением Клапейрона-Менделеева.
Вывод уравнения состояния газа впервые был сделан Б.П.Э. Клапейроном путем обобщения законов, установленных экспериментально выдающимися европейскими учеными на протяжении полутора столетий. Мы же интерпретируем эти законы как частные случаи уравнения (5.7). При  = const. получим закон Бойля-Мариотта, при
= const. получим закон Бойля-Мариотта, при 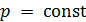 . – закон Гей-Люссака, а при
. – закон Гей-Люссака, а при  – закон Шарля. Прямым следствием (5.7) является также закон Авогадро. Приведем его формулировку.
– закон Шарля. Прямым следствием (5.7) является также закон Авогадро. Приведем его формулировку.
При одинаковых температурах и давлениях в равных объёмах любого газа содержится одинаковое число молекул.
При нормальных условиях (  ) это число задаётся постоянной Лошмидта
) это число задаётся постоянной Лошмидта 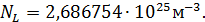
Парад законов, полученных «на кончике пера», является наилучшим подтверждением справедливости кинетической теории газов и ее основных представлений.
5.3. Уравнение эффузии
О явлении эффузии и применении молекулярных пучков в физических исследованиях мы неоднократно упоминали. Молекулярный пучок даёт возможность изучать не только статистические системы, но и изолированные атомы и молекулы.
Подобные исследования увенчались несколькими Нобелевскими премиями. Среди них отметим, например, опыты Штерна и Герлаха, приведшие к открытию спина и связанного с ним магнитного момента электрона; опыты Раби и его сотрудников, давшие возможность выполнить точные измерения магнитных моментов ядер; а также, опыты Куша и Лэмба, которым мы обязаны современным пониманием квантовой теории электромагнитных взаимодействий [13].
Явление эффузии описывается уравнением, которое определяет эффузионный поток через микроскопические и макроскопические параметры. Эффузионный поток 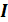 – это число частиц, протекающих за 1секунду через отверстие сечением
– это число частиц, протекающих за 1секунду через отверстие сечением 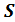 , диаметр которого
, диаметр которого 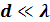 ,
, 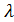 – средняя длина свободного пробега молекул
– средняя длина свободного пробега молекул

Уравнение (5.11) может быть получено способом, который мы использовали при выводе формулы давления (5.3).
Подставляя в уравнение (5.11) выражения для концентрации частиц 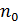 из (5.3) и средней скорости молекулы газа
из (5.3) и средней скорости молекулы газа 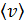 согласно (4.23), приведем его к виду
согласно (4.23), приведем его к виду
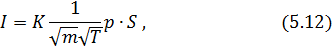
где 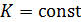 , ее значение нетрудно вычислить.
, ее значение нетрудно вычислить.
Уравнения (5.11) и (5.12) применяются при рассмотрении явлений переноса в вязких и ультра разряженных газах. Эти вопросы будут рассматриваться в конце лекционного курса.
Вывод уравнения эффузии включён в программу семинарских занятий.
5.4. Измерение давления
В научной и производственной практике в настоящее время требуется измерять давления в широком диапазоне от 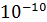 до
до 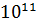 Па.
Па.
Методы измерения давления достаточно разнообразны, они изучаются в общем физическом практикуме. Здесь же на приведенной ниже схеме 5.4.1 дадим классификацию приборов для измерения давления в различных диапазонах.
Схема 5.4.1.
• Жидкостные (ртутные):
а) чашечные;
б) сифонные, в форме  – образных трубок.
Чувствительность до
– образных трубок.
Чувствительность до 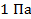 .
• Анероиды:
приёмной частью прибора является металлическая коробка, внутри которой создано разряжение. Под действием атмосферного давления коробка сжимается. Смещение стенки передается пружине и стрелке.
Чувствительность до
.
• Анероиды:
приёмной частью прибора является металлическая коробка, внутри которой создано разряжение. Под действием атмосферного давления коробка сжимается. Смещение стенки передается пружине и стрелке.
Чувствительность до 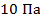 .
.
В зависимости от принципа действия и конструкции различают:
• Жидкостные;
• Поршневые;
• Деформационные или пружинные (трубчатые, мембранные).
Для измерения давления близкого к нулю применяют вакуумметры.Чаще всего это различные электрические манометры:
1. термоэлектрические,
2. ионизационные.
Барометры –
приборы для измерения атмосферного давления
Манометры –
приборы для измерения давления в широком диапазоне от 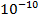 до
до 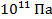 . Современные манометры часто представляют собой сложные измерительные устройства
. Современные манометры часто представляют собой сложные измерительные устройства
Первичные –
абсолютные приборы, которые непосредственно измеряют давление как величину равную отношению силы к площади.
Вторичные –
приборы, измеряющие некоторую величину, связанную с давлением.
Приборы для измерения давления
5.5. Определение и измерение температуры
Понятие температуры является одним из важнейших в молекулярной физике. Оно непростое, и его содержание для нас будет постепенно развиваться в процессе изучения дисциплины. В рамках микроскопической теории были разработаны два подхода к определению температуры (4.5) и (4.20). Эти подходы несут разные смыслы, но определяют одну величину. Возникает вопрос, что же мы измеряем термометром?
Эмпирически температура определяется как мера «нагретости» тела.
Температура является косвенно измеряемой величиной.Её измерение сводится к измерению некоторой величины, характеризующей тело, которая изменяется с изменением его «нагретости». Тело, выбираемое для измерения «нагретости» называется термометрическим, а величина, посредством которой измеряют температуру – называется термометрической величиной. Устройство термометров различается прежде всего по этим параметрам (см. схему 5.5.1). Для проведения процедуры измерения необходимо установление температурной шкалы. Построение эмпирических шкал в свою очередь требует определения особых реперных точек, т.е. неизменных воспроизводимых температур.
Все эти аспекты мы рассмотрим на примере построения эмпирической шкалы газового термометра.
Схема 5.5.1.
Виды термометров
Газовые термометры (первичные):
служат для калибровки вторичных термометров.
Термометрическая величина – давления газа.
Жидкостные термометры:
ртутный, спиртовой пентановый и др.
Термометрическая величина – объем жидкости.
Пирометры – приборы, с помощью которых измеряется энергия излучения нагретого тела, по которой делается вывод о его температуре.
Термометрическая величина – интенсивность испускаемого телом излучения.
Термометры сопротивления:
Термометрическая величина –
электрическое сопротивление
металлического или полупроводникового резистора.
Термопары: медь-константан, хромель-алюмель, платина-платинородий.
Термометрическая величина – разность потенциалов на однородных концах термопары (эффект Зеебека).
Для измерения низких температур (порядка 1 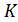 ) используется измерение магнитных свойств тела при данной температуре.
) используется измерение магнитных свойств тела при данной температуре.
Термометрическая величина – магнитная восприимчивость парамагнитной соли 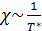 .
.
5.6. Построение эмпирической шкалы на основе газового термометра
Эмпирическая температура при фиксированной шкале и условленных реперных точках не одинакова при различном выборе термометрического тела и термометрической величины. Это означает, что различные термометры при измерении температуры одного и того же тела будут давать, как правило, разные показания.
Для разрешения данной проблемы за основной термометр был принят газовый, по которому было решено градуировать все остальные термометры. Причины выбора в качестве основного газового термометра указаны ниже.
Преимущества газовой шкалы температур
Идеальные газы (достаточно разрежённые реальные газы) с большой точностью подчиняются закону Бойля-Мариотта:
произведение объёма V данной массы газа на его давление p зависит только от температуры:

где C – постоянная, зависящая от массы и химической природы газа.
Если для идеального газа 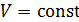 , то в этом случае вторым независимым законом идеальных газов наряду с законом Бойля-Мариотта следует считать закон Шарля:
, то в этом случае вторым независимым законом идеальных газов наряду с законом Бойля-Мариотта следует считать закон Шарля:

Опытным путём доказано, что температура T , определённая по формулам (5.13) и (5.14), очень слабо зависит от химической природы газа, которым наполнен резервуар газового термометра. Таким образом, показания различных газовых термометров при измерении температуры одного и того же тела очень мало отличаются друг от друга.
Построение газовой шкалы температур
Газовый термометр можно реализовать двумя способами. В одном из них объём газа 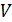 поддерживается постоянным. Термометрической величиной служит давление
поддерживается постоянным. Термометрической величиной служит давление 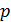 . В другом случае поддерживается постоянное давление газа, измерение температуры сводится к измерению объёма. Принципиально оба способа равноправны, но первый способ наиболее удобен, поэтому и применяется на практике.
. В другом случае поддерживается постоянное давление газа, измерение температуры сводится к измерению объёма. Принципиально оба способа равноправны, но первый способ наиболее удобен, поэтому и применяется на практике.
Газовый термометр представляет собой стеклянный, кварцевый или металлический баллон, заполненный азотом или гелием и соединенный с манометром с помощью капилляра. По показаниям манометра производится расчет измеряемой температуры.
Для построения идеально-газовой шкалы температур в качестве реперных точек рассматриваются нормальные точки кипения и замерзания воды  и
и  , соответственно. Градус температуры выбирают таким, чтобы выполнялось условие
, соответственно. Градус температуры выбирают таким, чтобы выполнялось условие

Для некоторой массы газа измеряют давления 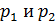 , соответствующие
, соответствующие 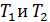 . Полученное в эксперименте отношение давлений равно 1,3661. Следовательно
. Полученное в эксперименте отношение давлений равно 1,3661. Следовательно
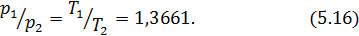
Совместное решение (5.15) и (5.16) дает: 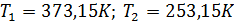 .
.
Таким образом, газовая шкала температур полностью определена.
Термодинамическая шкала температур
Температуры кипения и замерзания воды зависят от давления, к тому же фиксируются с недостаточной точностью, поэтому в СИ условились определять шкалу температур по одной реперной точке – тройной точке воды.Это единственное состояние, когда в равновесии находятся три фазы (жидкая, газообразная и твёрдая), при строго определённых значениях  и
и 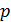 .
.
В термодинамической шкале температур или шкале Кельвина температура реперной точки, по определению, принята равной 273,16 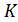 .
.
Единица температуры определяется как 1/273,16 температурного интервала между тройной точкой и точкой абсолютного нуля, которая на 273,16  ниже температуры тройной точки воды.
ниже температуры тройной точки воды.
Если используется газовый термометр, то температуру можно определить по формуле

где 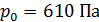 – давление в тройной точке воды. Поскольку
– давление в тройной точке воды. Поскольку 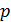 всегда положительная величина, то и параметр
всегда положительная величина, то и параметр  не может принимать отрицательного значения. Абсолютный нуль является самой низкой из возможных температур. Единицу измерения температуры в этой шкале называют кельвином (сокращенно
не может принимать отрицательного значения. Абсолютный нуль является самой низкой из возможных температур. Единицу измерения температуры в этой шкале называют кельвином (сокращенно  ) в честь английского физика лорда Кельвина, предложившего термодинамическую шкалу температур, тождественную с идеальной газовой шкалой. Важно отметить, что поскольку (5.17) основана на уравнении состояния идеального газа, то температура
) в честь английского физика лорда Кельвина, предложившего термодинамическую шкалу температур, тождественную с идеальной газовой шкалой. Важно отметить, что поскольку (5.17) основана на уравнении состояния идеального газа, то температура  определенная этой формулой совпадает с
определенная этой формулой совпадает с  , которая была введена как обозначение в микроскопической теории.
, которая была введена как обозначение в микроскопической теории.
Наряду с абсолютной температурной шкалой в физике и в повседневной жизни применяются эмпирические шкалы, такие как шкала Цельсия, шкала Фаренгейта и шкала Реомюра. В этих шкалах величины градусов различны, поскольку реперным точкам приписываются разные температуры. Однако, если взять одно и то же термометрическое тело и одну и ту же термометрическую величину, то можно получить формулы пересчета температур от одной шкалы к другой: 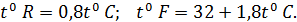
Контрольные вопросы
1. Дайте определение величине давления газа на стенку сосуда.
2. Почему при выводе формулы для давления газа можно использовать одномерное распределение Максвелла?
3. Чему равна нормальная составляющая передаваемого одной молекулой стенке сосуда при столкновении с ней?
4. Как подсчитать число частиц, сталкивающихся со стенкой сосуда единичной площади за одну секунду, если составляющая скорости в направлении к стенке принадлежат интервалу ( 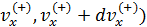 ?
?
5. Обоснуйте законы Паскаля и Дальтона.
6. Какое уравнение называют основным уравнением МКТ? Запишите его.
7. Запишите уравнение Клапейрона-Менделеева.
8. Сформулируйте закон Авогадро.
9. Что называется уравнением эффузии? Запишите его.
10. Какие приборы используются для измерения давления газа в разных диапазонах?
11. Какие величины являются термометрическими в таких термометрах как газовый, жидкостный, термопара?
12. Какая реперная точка используется при построении шкалы Кельвина? Чему равна её температура?
ЛЕКЦИЯ 6
РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНА
6.1. Распределение молекул по энергиям во внешнем потенциальном поле
До сих пор мы в своём воображении заботливо оберегали молекулярные системы от воздействия на них внешних силовых полей. Пространство было изотропным, а средняя концентрация молекул газа в состоянии термодинамического равновесия была всюду одинаковой. Наличие внешнего силового поля меняет ситуацию коренным образом. Поле оказывает существенное влияние на распределение частиц в пространстве. При выводе закона вероятностей Гиббса (см. 4.1) отмечалось, что область применимости этого закона может включать в себя силовое поле. Важно, чтобы его существование было совместимо с состоянием термодинамического равновесия молекулярной системы. Если энергия частицы в силовом поле зависит от её скорости или явно от времени, то такое поле не может привести систему к стационарному состоянию. Можно ожидать, что к благополучному исходу приводят потенциальные поля, в которых энергия частицы зависит от её координат. В действительности, потенциальный характер поля является необходимым, но не достаточным условием равновесного состояния системы. Анализ показывает, что среди подходящих потенциальных полей есть и хорошо вам известные: однородное гравитационное поле, поле центробежных сил и электростатическое поле.
Полная энергия системы  молекулы идеального газа, находящегося во внешнем потенциальном поле, равна сумме кинетической энергии
молекулы идеального газа, находящегося во внешнем потенциальном поле, равна сумме кинетической энергии 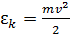 и потенциальной энергии
и потенциальной энергии 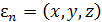 . Эти величины зависят от разных переменных, поэтому вероятности состояний молекулы
. Эти величины зависят от разных переменных, поэтому вероятности состояний молекулы 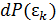 и
и 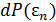 являются независимыми, и могут рассматриваться по отдельности. Рассмотрение
являются независимыми, и могут рассматриваться по отдельности. Рассмотрение 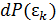 привело (см. 4.2) к распределению Максвелла. Распределение вероятностей по потенциальной энергии
привело (см. 4.2) к распределению Максвелла. Распределение вероятностей по потенциальной энергии 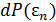 носит название распределения Больцмана и является предметом нашего обсуждения теперь.
носит название распределения Больцмана и является предметом нашего обсуждения теперь.
Распределение Больцмана отвечает на вопрос: какова вероятность того, что потенциальная энергия молекулы идеального газа, находящегося в состоянии термодинамического равновесия, лежит в интервале значений энергии от 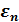 до
до 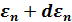 ? Его явный вид можно получить из распределения Гиббса согласно (4.10), полагая, что
? Его явный вид можно получить из распределения Гиббса согласно (4.10), полагая, что 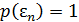 .
.

Постоянная 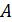 , как обычно находится из условия нормировки. Формула (6.1) позволяет решать стандартные задачи статистики: нахождение
, как обычно находится из условия нормировки. Формула (6.1) позволяет решать стандартные задачи статистики: нахождение 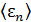 и среднего числа частиц, обладающих потенциальной энергией в её доступных интервалах.
и среднего числа частиц, обладающих потенциальной энергией в её доступных интервалах.
При решении многих задач удобнее использовать не вероятность (6.1), а связанную с ней пространственную концентрацию частиц 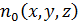 .
.
6.2. Формула Больцмана для концентрации молекул в потенциальном поле
Формулы для концентрации можно получить из (6.1), перейдя от переменной 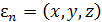 непосредственно к координатам молекулы
непосредственно к координатам молекулы
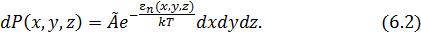
Если система состоит из 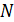 частиц, то их среднее число
частиц, то их среднее число 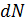 в элементарном объёме
в элементарном объёме 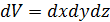 вблизи точки
вблизи точки 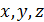 равно
равно
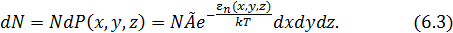
Чтобы получить локальную концентрацию молекул 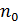 в точке, разделим
в точке, разделим 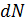 на элементарный объём
на элементарный объём
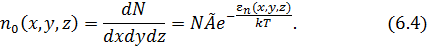
Объединив константы перед экспонентой, запишем окончательный вид формулы для пространственной концентрации молекул в потенциальном поле
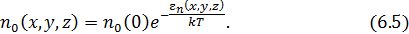
Новая константа 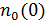 равна концентрации молекул в том месте, где
равна концентрации молекул в том месте, где 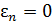 .
.
Она может быть легко определена, если известна концентрация частиц, хотя бы в одной точке пространства. При отсутствии такой информации постоянную 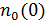 находят из условия нормировки на полное число частиц
находят из условия нормировки на полное число частиц 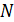 в заданном объёме
в заданном объёме 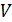 :
:
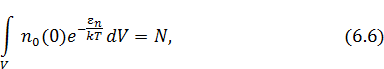

Дата добавления: 2015-08-11; просмотров: 2584;
