I. ОСНОВЫ МОЛЕКУЛЯРНОЙ СТАТИСТИКИ 4 страница
5. Докажите, что биномиальное распределение отвечает условию нормировки?
6. Выделите основные признаки случайных событий, которые описывает закон Бернулли? Приведите примеры.
7. Чему равно наиболее вероятное значение 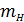 и среднее значение
и среднее значение 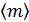 ?
?
8. Чему равна дисперсия числа частиц 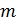 в объёме
в объёме 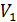 ?
?
9. Как зависит относительная флуктуация числа частиц от соотношения объёмов 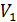 и
и 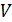 ?
?
10. Запишите распределение Пуассона. Представьте его графически. Какие явления оно описывает?
11. Запишите распределение Гаусса. Представьте его графически. Какие явления оно описывает?
12. В чём заключается явление эффузии. Какой статистический закон применим для её описания?
ЛЕКЦИЯ 4
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
4.1. Распределение энергии в статической системе
Одной из важнейших проблем молекулярной физики является вопрос о распределении энергии между отдельными частями изолированной системы. Первые теоретические исследования в этой области были проведены в середине XIX века английским физиком Джеймсом Кларком Максвеллом и австрийским учёным Людвигом Больцманом. Максвелл получил распределение молекул идеального газа по скоростям и, соответственно, по кинетическим энергиям. Больцман вывел, закон распределения частиц по энергиям во внешнем потенциальном поле. В те годы базовые понятия молекулярной статистики только начинали формироваться, канонов получения статических распределений не было. Поэтому учёные искали и находили оригинальные способы решения частных задач. В 1859 году Максвелл предложил достаточно сложный метод вывода своей знаменитой формулы. Чтобы не преодолевать трудности авторского подхода, мы обратимся к другому, более современному способу нахождения распределения.
Сорок лет спустя после открытия Максвелла американский физик-теоретик Джозайя Уиллард Гиббс вывел общий закон распределения энергии между подсистемами изолированной системы. Его метод поражает своей универсальностью и математической простотой. Поэтому сначала выведем распределение Гиббса, а затем получим закон Максвелла как его частный случай, когда подсистемой является одна частица, обладающая только кинетической энергией.
В дальнейшем нам предстоит ещё не раз обращаться к распределению Гиббса за поддержкой в обосновании законов молекулярной статистики.
Вывод распределения Гиббса
Описание системы
Рассмотрим систему, принадлежащую микроканоническому ансамблю, тогда любая её часть – подсистема, принадлежит каноническому ансамблю (рис. 4.1).
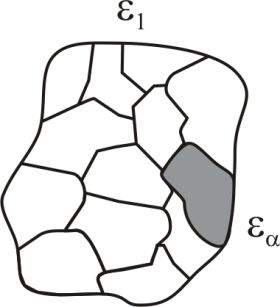
|
Введем обозначения:  – полная энергия системы;
– полная энергия системы; 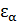 – энергия подсистемы;
– энергия подсистемы; 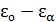 – энергия оставшейся части системы.
– энергия оставшейся части системы.
Актуальные свойства модели системы
• Система находится в состоянии термодинамического равновесия.
• Наличие силовых полей возможно, если это совместимо с состоянием термодинамического равновесия.
• Структура подсистемы произвольна, её энергия может меняться дискретно или непрерывно.
• Единственное ограничение, которое должно выполняться всегда

Постановка задачи
Какова вероятность того, что рассматриваемая подсистема находится в состоянии с энергией 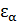 ?
?
Вывод закона
Определение вероятности макросостояния (2.15) справедливо для системы, принадлежащей микроканоническому ансамблю, поэтому будем определять вероятность состояния подсистемы через микроскопические состояния всей системы.
Для простоты предположим, что энергия подсистемы меняется дискретно.
• Запишем вероятность интересующего нас макроскопического состояния системы

где 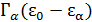 – число микросостояний всей системы, посредством которых осуществляется состояние с энергией
– число микросостояний всей системы, посредством которых осуществляется состояние с энергией 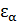 у подсистемы, а
у подсистемы, а 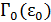 – полное число микросостояний системы.
– полное число микросостояний системы.
• Используя очевидное соотношение 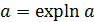 ,
,
преобразуем (4.2)
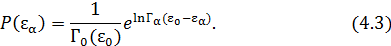
Поскольку 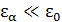 , а логарифм – медленно меняющаяся функция, разложим его в ряд Тейлора в точке
, а логарифм – медленно меняющаяся функция, разложим его в ряд Тейлора в точке 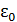 по малому параметру
по малому параметру 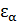 , ограничившись в разложении линейным членом:
, ограничившись в разложении линейным членом:
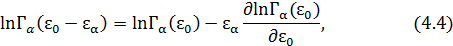
здесь 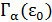 – число микросостояний всей системы, посредством которых осуществляется состояние с нулевой энергией у рассматриваемой подсистемы.
– число микросостояний всей системы, посредством которых осуществляется состояние с нулевой энергией у рассматриваемой подсистемы.
• Введём обозначение для производной

С увеличением энергии обычной физической системы число доступных ей микросостояний растёт, причём, крайне быстро, поэтому постоянная  - положительная величина. Она является характеристикой, как подсистемы, так и всей системы, находящейся в состоянии термодинамического равновесия. Через это фундаментальное свойство в статистике вводится термодинамическая температура:
- положительная величина. Она является характеристикой, как подсистемы, так и всей системы, находящейся в состоянии термодинамического равновесия. Через это фундаментальное свойство в статистике вводится термодинамическая температура:

где 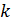 – коэффициент пропорциональности, называется постоянной Больцмана. Определение температуры (4.5–4.6) будем называть «первичным» или «из первых принципов». Существуют и другие способы определения температуры в молекулярной теории. Скоро вы с ними познакомитесь.
– коэффициент пропорциональности, называется постоянной Больцмана. Определение температуры (4.5–4.6) будем называть «первичным» или «из первых принципов». Существуют и другие способы определения температуры в молекулярной теории. Скоро вы с ними познакомитесь.
• Подставив выражение (4.4) в (4.3), используя параметр  , получаем
, получаем
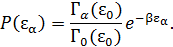
Постоянный множитель 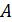 находится из условия нормировки вероятностей.
находится из условия нормировки вероятностей.
Ответ:

Если энергия подсистемы меняется непрерывно, то её значение фиксируется как  , принадлежащая интервалу
, принадлежащая интервалу  ,
, 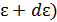 . В этом случае распределение записывается в виде
. В этом случае распределение записывается в виде

При выводе распределения Гиббса (его также называют каноническим распределением) мы по умолчанию полагали, что к состоянию с энергией 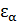 приводит только одно микроскопическое состояние подсистемы.
приводит только одно микроскопическое состояние подсистемы.
Если это не так, то формулы (4.7) и (4.8) следует дополнить соответствующими множителями.
На схеме 4.1.1 приведены обобщенные формулы Гиббса для дискретного и непрерывного распределения энергии.
Схема 4.1.1.
Дискретное распределение энергии подсистемы:
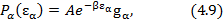 где
где 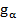 – кратность вырождения состояния с энергией
– кратность вырождения состояния с энергией 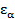 или его статистический вес, - число микроскопических состояний подсистемы, приводящих к состоянию с фиксированным значением
или его статистический вес, - число микроскопических состояний подсистемы, приводящих к состоянию с фиксированным значением 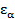 .
.
Непрерывное распределение энергии подсистемы:
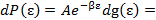
 где
где 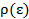 - плотность состояний с энергией
- плотность состояний с энергией 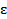 на интервале
на интервале 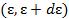 .
.
Обобщённые формулы распределения Гиббса
4.2. Вывод распределения Максвелла
Описание системы
Система представляет собой классический идеальный газ, состоящий из тождественных частиц, в состоянии термодинамического равновесия. Внешние силовые поля отсутствуют. В качестве подсистемы рассматривается одна молекула, которая может обмениваться энергией с другими подсистемами (молекулами) в результате столкновений.
Актуальные свойства модели системы
• Подсистем – молекул очень большое число, следовательно, условие
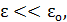
выполняется, поэтому для вывода закона можем использовать распределение Гиббса.
• Поскольку силовых полей нет, частица обладает только кинетической энергией

Постановка задачи
Какова вероятность 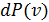 того, что частица обладает абсолютной скоростью
того, что частица обладает абсолютной скоростью 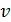 в интервале
в интервале 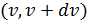 ?
?
Вывод закона
• По условию частица обладает только кинетической энергией, зависящей от абсолютной скорости (4.11), поэтому удобно перейти к новому аргументу 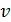
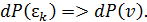
Следуя (4.10), запишем:
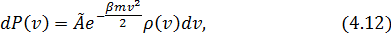
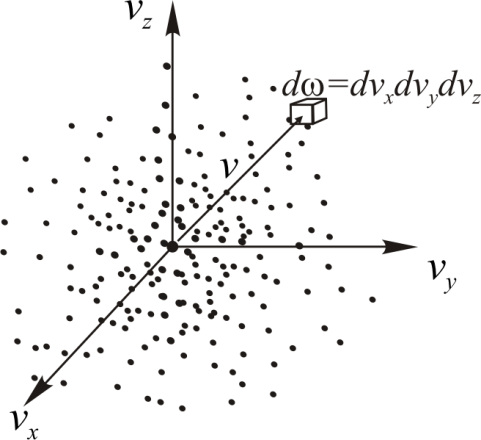
где 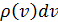 – число микросостояний, которые приводят частицу к одной и той же абсолютной скорости. Для его нахождения нам придётся вообразить пространство скоростей. Этот приём использовал Максвелл в своих оригинальных работах.
– число микросостояний, которые приводят частицу к одной и той же абсолютной скорости. Для его нахождения нам придётся вообразить пространство скоростей. Этот приём использовал Максвелл в своих оригинальных работах.
• Рассмотрим прямоугольную систему координат с осями 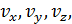 в которой отложим все возможные векторы скоростей любой молекулы газа. Концы этих векторов – скоростные точки. Совокупность всех скоростных точек образует трёхмерное пространство – пространство скоростей (рис. 4.2). Вследствие равноправности всех направлений движения расположение точек относительно начала координат будет сферически симметричным. Поэтому плотность точек может зависеть только от модуля скорости
в которой отложим все возможные векторы скоростей любой молекулы газа. Концы этих векторов – скоростные точки. Совокупность всех скоростных точек образует трёхмерное пространство – пространство скоростей (рис. 4.2). Вследствие равноправности всех направлений движения расположение точек относительно начала координат будет сферически симметричным. Поэтому плотность точек может зависеть только от модуля скорости  , а не от её направления
, а не от её направления
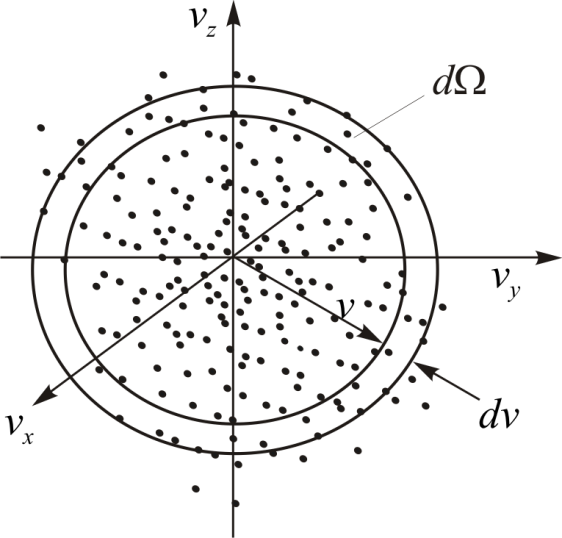
Рис. 4.2.
• Число микросостояний с абсолютной скоростью 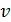 в интервале
в интервале
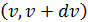 пропорционально объёму бесконечно тонкого шарового слоя со средним радиусом
пропорционально объёму бесконечно тонкого шарового слоя со средним радиусом 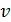 и толщиной
и толщиной 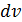 (рис. 4.2).
(рис. 4.2).
Объём этого слоя равен

следовательно,

• Подставим (4.14) в (4.12), тогда
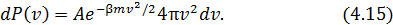
Постоянная 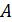 , это произведение двух констант
, это произведение двух констант 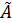 и
и 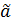 . Её значение находится из условия нормировки вероятностей
. Её значение находится из условия нормировки вероятностей
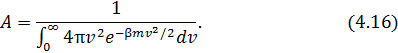
Вычислив интеграл в знаменателе (4.16), получим
ответ:
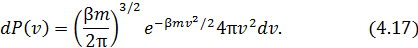
Эта формула представляет собой закон распределения Максвелла по абсолютным значениям скорости.
Прежде чем переходить к анализу полученной формулы проясним значение параметра  .
.
Найдём среднюю кинетическую энергию молекулы:
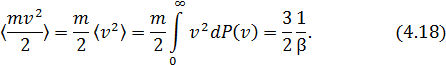
Таким образом,  характеризует важнейшую величину статистической системы – среднюю кинетическую энергию молекул.
характеризует важнейшую величину статистической системы – среднюю кинетическую энергию молекул.
Используя формальное определение температуры (4.6) запишем


Формулы (4.19, 4.20) являются основными определениями температуры в статистике. Из них следует, что температура – это мера средней кинетической энергии молекул.
4.3. Плотность вероятности и характерные скорости распределения Максвелла
Плотность вероятности распределения (4.17) обозначим как 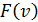 и запишем её в явном виде, используя определение температуры,
и запишем её в явном виде, используя определение температуры,
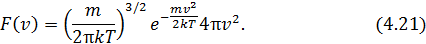
Примерный вид 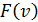 для различных температур приведён на рис. 4.3. Борьба двух противоположных тенденций, а именно, убывание вероятности состояний с ростом скорости и возрастание плотности состояний приводят к образованию максимума функции и несимметричной форме колокольчика на графике.
для различных температур приведён на рис. 4.3. Борьба двух противоположных тенденций, а именно, убывание вероятности состояний с ростом скорости и возрастание плотности состояний приводят к образованию максимума функции и несимметричной форме колокольчика на графике.
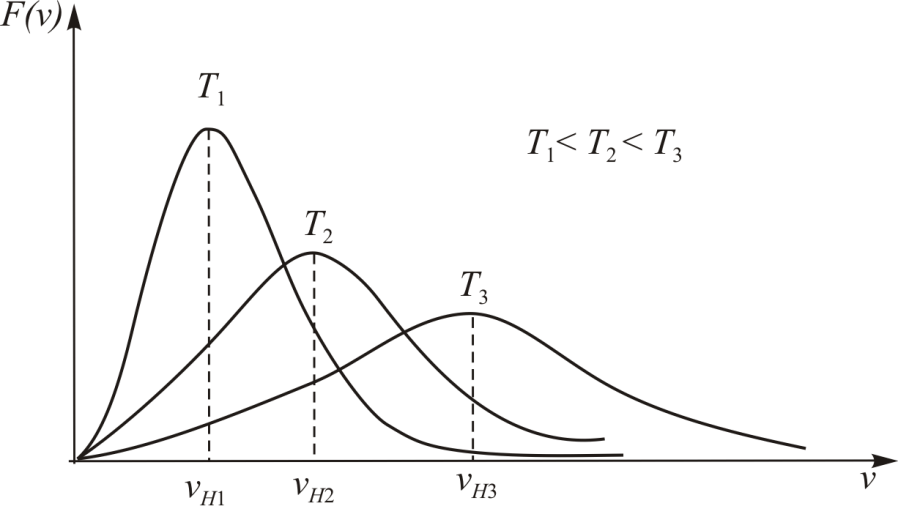
Рис. 4.3.
С увеличением температуры максимум функции 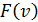 смещается в сторону больших скоростей, а его величина уменьшается, при этом площадь под каждой кривой остаётся равной единице.
смещается в сторону больших скоростей, а его величина уменьшается, при этом площадь под каждой кривой остаётся равной единице.
Схема 4.3.1.
| Характерные скорости распределения Максвелла | ||
Наиболее вероятная скорость 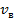 . .
| Средняя скорость
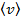
| Средняя квадратичная скорость 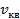 . .
|
Соответствует максимуму функции 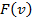 и определяется из условия и определяется из условия 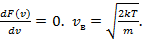
| По определению среднего
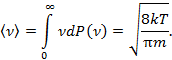
| 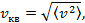
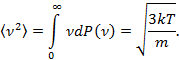
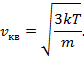
|
Обратите внимание, что все три характерные скорости пропорциональны, их числовые коэффициенты имеют очень близкие значения и находятся в пределах от 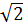 до
до 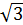 .
.
Характерные скорости молекул азота и кислорода при температуре T=300K равны примерно 400 – 500 м/с. Их величины сравнимы со скоростью звука в воздухе.
4.4. Распределение Максвелла по компонентам скорости
Формальный переход от сферической системы координат в пространстве скоростей (рис. 4.2) к декартовой (рис. 4.4) приводит закон Максвелла к следующему виду:

 Это распределение отвечает на вопрос: какова вероятность того, что молекула обладает скоростью с компонентами
Это распределение отвечает на вопрос: какова вероятность того, что молекула обладает скоростью с компонентами 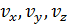 в интервалах
в интервалах 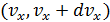 ,
, 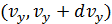 ,
, 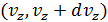 ?
?
Как видно из (4.25), вероятность выражается произведением одномерных вероятностей, поскольку по своей сути является вероятностью произведения трех независимых событий:
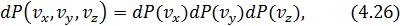
где
| Рис. 4.4. |
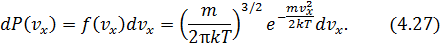
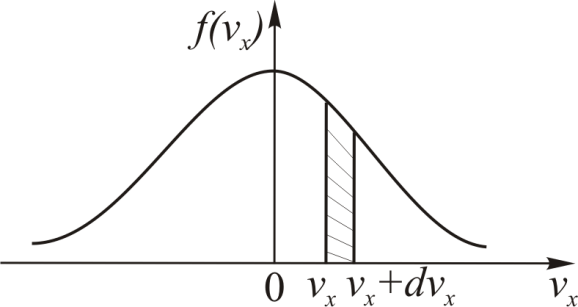 Аналогичный вид имеют вероятности
Аналогичный вид имеют вероятности 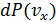 и
и 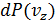 . Одномерная плотность вероятности типа
. Одномерная плотность вероятности типа 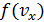 совпадает с гауссовской функцией распределения и на графике (рис.4.5) изображается симметричным колокольчиком.
совпадает с гауссовской функцией распределения и на графике (рис.4.5) изображается симметричным колокольчиком.
| Рис. 4.5. |
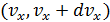 .
.
Приведённые выше формулы распределения Максвелла для сферической и декартовой систем координат позволяют находить средние значения различных микроскопических и макроскопических параметров, зависящих от абсолютной скорости или отдельных компонент скорости в соответствии с общей процедурой усреднения.
Для применения этих формул к системе 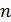 частиц необходимо использовать теорему о сложении вероятностей. Число частиц, скорости которых заключены между
частиц необходимо использовать теорему о сложении вероятностей. Число частиц, скорости которых заключены между 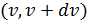 ,
,

Относительное число частиц со скоростями в том же интервале

Применение одномерного распределения к системе частиц даёт соответствующие формулы, определяющие абсолютное и относительное количество частиц с компонентами скорости 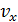 , заключёнными в интервале
, заключёнными в интервале  .
.
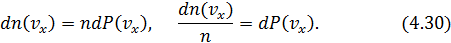
Таким образом, абстрактная величина вероятности проявляется в конкретной и ясной форме: это не что иное, как доля частиц, обладающих той или иной скоростью.
4.5. Экспериментальная проверка распределения Максвелла
Закон Максвелла неоднократно подвергался экспериментальной проверке, начиная с опыта Штерна, осуществлённого в 1920 году. В большинстве опытов используется такое явление как эффузия. С помощью нескольких щелей получают узкий молекулярный пучок, который направляется на устройство, сортирующее молекулы по скоростям, после чего частицы регистрируют тем или иным способом. Для сортировки молекул наиболее часто используют метод вращающихся дисков (опыт Ламмерта) и метод вращающегося цилиндра (опыт Цартмана).
На схеме 4.5.1 дано краткое описание этих методов. Более подробное их описание можно найти в [14].
Существуют и принципиально иные способы проверки данного закона. Например, наблюдается экспериментально уширение линии спектра излучения, движущихся возбуждённых молекул газа за счёт эффекта Допплера. Ширина спектральных линий определяется распределением молекул по скоростям.
Схема 4.5.1.
| Измерительная схема Цартмана |
| Измерительная схема Ламмерта |
Для сортировки молекул по скоростям используется вращающийся цилиндр со щелью:
 Когда щель попадает на линию пучка, через неё внутрь цилиндра входит порция молекул.
Молекулы с различными скоростями достигают противоположной стенки цилиндра с различным запаздыванием по отношению к моменту прохождения щели и поэтому попадают на разные участки внутренней стенки цилиндра. Точка попадания на стенке смещается против вращения на расстояние
Когда щель попадает на линию пучка, через неё внутрь цилиндра входит порция молекул.
Молекулы с различными скоростями достигают противоположной стенки цилиндра с различным запаздыванием по отношению к моменту прохождения щели и поэтому попадают на разные участки внутренней стенки цилиндра. Точка попадания на стенке смещается против вращения на расстояние
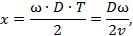 где
где 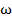 - угловая скорость вращения цилиндра, - угловая скорость вращения цилиндра, 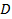 - его диаметр; - его диаметр; 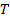 – время пролета молекулы от щели до стенки со скоростью – время пролета молекулы от щели до стенки со скоростью 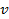 . .
|
| Измеряя число молекул, попавших на различные участки, внутренней поверхности цилиндра можно вычислить распределение молекул в пучке по скоростям. |
| Измеряя число молекул, прошедших сквозь щели в каждом опыте, вычисляют распределение молекул по скоростям. |
| Регистрация молекул производится различными методами в зависимости от иx свойств. В простейшем случае они осаждаются на стеклянную пластинку и по степени прозрачности пластинки, измеряемой фотометрированием, можно судить об их числе. |
Для сортировки молекул по скоростям используется метод вращающихся дисков с щелями вдоль радиуса:
 Если щели повёрнуты на угол
Если щели повёрнуты на угол  относительно друг друга, то при угловой скорости относительно друг друга, то при угловой скорости 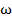 диски повернутся на угол диски повернутся на угол  в течение промежутка времени Δt=φ/ω. Поэтому через обе щели, расстояние между которыми в течение промежутка времени Δt=φ/ω. Поэтому через обе щели, расстояние между которыми 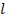 , пройдут молекулы со скоростью , пройдут молекулы со скоростью 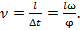 Меняя
Меняя 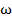 (или (или 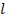 ) можно пропускать молекулы с разными (определёнными) скоростями ) можно пропускать молекулы с разными (определёнными) скоростями
|
Опытные проверки блистательно подтвердили справедливость распределения Максвелла.
Контрольные вопросы
1. На какой вопрос отвечает распределение Гиббса? Какова область его применимости?
2. Как используется условие 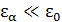 при выводе закона Гиббса?
при выводе закона Гиббса?
3. Как определяется параметр  в распределении Гиббса?
в распределении Гиббса?
Какие существуют основания считать, что 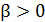 ?
?
4. Запишите распределение Гиббса в обобщенной форме, если энергия системы является
а) непрерывной случайной величиной;
б) дискретной случайной величиной. Поясните смысл всех сомножителей в формуле.
5. На какой вопрос отвечает распределение Максвелла?
6. Что называется пространством скоростей? С какой целью эта модель используется при выводе распределения Максвелла?
7. Как вычислить нормировочную постоянную 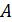 в формуле Максвелла?
в формуле Максвелла?
8. Как определяется температура в статистике?
9. График плотности вероятности 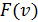 выглядит как асимметричный колокольчик, а график
выглядит как асимметричный колокольчик, а график 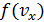 – как симметричный колокольчик. С чем это связано?
– как симметричный колокольчик. С чем это связано?
10. Какие скорости молекул называются характерными? Чему они равны?
11. Как определить долю частиц в системе, обладающих абсолютной скоростью в интервале 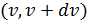 ?
?
12. Как осуществлялась проверка распределения Максвелла в опыте Цартмана и в опыте Ламмерта?
ЛЕКЦИЯ 5
МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ И МАКРОСКОПИЧЕСКИЕ ИЗМЕРЕНИЯ
Критерием справедливости или истинности любой физической теории является эксперимент. Напомним, что одной из основных задач молекулярной статистики является установление связи между средними микроскопическими параметрами молекулярной системы и её макроскопическими характеристиками. Все макроскопические параметры системы могут быть получены из микроскопическихпредставлений, но их экспериментальное определение требует макроскопических измерений.
Начнём с рассмотрения такого макроскопического параметра как давление. По определению, давление – это отношение силы, действующей нормально к поверхности, к величине этой поверхности. Силу можно выразить через изменение импульса:

В газе импульс 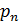 передаётся стенке молекулами, сталкивающимися с ней. Таким образом, из (5.1) следует, что давление газа – это величина, численно равная нормальной составляющей импульса, передаваемого молекулами газа за 1 секунду стенке сосуда площадью 1 квадратный метр. Исходя из этого заключения, проведём расчёт давления газа.
передаётся стенке молекулами, сталкивающимися с ней. Таким образом, из (5.1) следует, что давление газа – это величина, численно равная нормальной составляющей импульса, передаваемого молекулами газа за 1 секунду стенке сосуда площадью 1 квадратный метр. Исходя из этого заключения, проведём расчёт давления газа.
5.1. Вывод формулы для давления идеального газа
Описание системы
Рассматриваемая система – идеальный газ, который находится в сосуде в состоянии термодинамического равновесия. Внешних силовых полей нет.
Постановка задачи
На основе микроскопических представлений требуется получить уравнение, определяющее давление 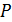 .
.
Актуальные свойства модели системы
Распределение молекул идеального газа по скоростям подчиняется закону Максвелла. Поскольку вклад в давление вносят только нормальные к стенке составляющие импульсов молекул, то для предстоящих расчетов потребуется применение одномерного распределения по компоненте скорости. Отсутствие внешних воздействий позволяет считать концентрацию частиц одинаковой во всех частях сосуда.
Дата добавления: 2015-08-11; просмотров: 3409;
