ПРИБЛИЖЕНИЕ СИЛЬНОЙ СВЯЗИ
 |
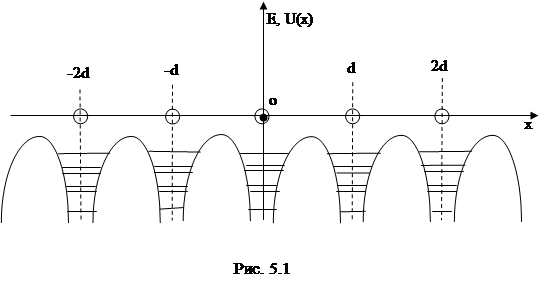Рассмотрим случай, когда электроны находятся в монокристалле, то есть в периодическом потенциальном поле положительных ионов, располагающихся в узлах кристаллической решетки. Линейная цепочка положительных ионов в некотором направлении Х кристалла образует для электронов потенциальный рельеф, показанный на рисунке 5.1.
Изолированные атомы имеют аналогичные потенциальные ямы для электронов, однако отличаются тем, что верхние части кривых приближаются к горизонтальной оси, уходя в бесконечность (глава I). При сближении атомов за счет их взаимодействия видоизменяется верхняя часть кривых, и создаются потенциальные барьера с вершинами, лежащими ниже U =0. Глубина потенциальных ям принципиального значения не имеет, поэтому потенциальной рельеф, представленный на рис. 5.1. Заменяют рельефом с конечной глубиной ям. Кроме того барьеры, разделяющие электроны соседних атомов выбирают прямоугольной формы (рис. 5.2).
Описанную модель потенциального рельефа называют моделью Кронига-Пени.
Предположим вначале, что при создании линейной цепочки атомов все электроны находятся в потенциальных ямах «своих» атомов. Взаимодействие атомов приводит к уменьшению высоты и ширины потенциальных барьеров, что делает возможным туннелирование электронов. Наибольшая вероятность туннельного эффекта существует для внешних электронов, для которых высота барьера U-E минимальна (рис. 5.1). Примем в модели потенциального рельефа дно ямы за начало отсчета потенциальной энергии (рис. 5.2).
При движении электрона в яме со скоростью V за одну секунду осуществляется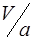 
подходов к барьеру. Частоту туннельных переходов электронов из одного атома цепочки в другой найдем умножив частоту подходов к барьеру на вероятность туннельного эффекта:
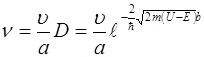(5.2)
Время пребывания электрона в пределах атома равно обратной величине, то есть
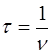(5.3)
Положим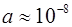 
см (размер атома), 
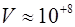см/сек (скорость теплового движения электрона), 
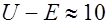эВ (энергия ионизации, например атома Na), 
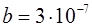см ( расстояние между изолированными атомами).
Из (5.2) и (5.3) находим 
с-1, 
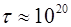лет.
Следовательно, в системе изолированных атомов вероятность туннельного эффекта ничтожно мала даже для валентных электронов.
Если учесть, что для линейной цепочки атомов в кристалле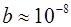 
см, то при сохранении прежних значений для a, V, U-E, находим 
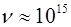c-1 и 
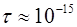с.
При столь высокой частоте переходов валентных электронов от атома к атому не имеет смысла связывать их с определенным атомом. Таким образом, туннельный эффект приводит к «обобществлению» валентных электронов.
В соответствии с принципом неопределенностей оценим неопределенность в значении энергии валентных электронов
.
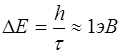Это означает, что энергетический уровень валентных электронов, имеющий в изолированном атоме ширину ~10-7 эВ, превращается в кристалле в энергетическую зону шириной порядка единиц эВ.
 |
Для электронов внутренних оболочек вследствие резкой зависимости от расстояния ширины и высоты барьера (рис. 5.1) вероятность туннельного эффекта низка. Энергетические уровни этих электронов в кристалле такие же узкие как и в атоме. На рис. 5.3 в качестве примера показано изменении энергетических уровней атомов натрия при их сближении.
При расстоянии между атомами натрия равному межатомному расстоянию в кристалле (r = d) уровни 1S и 2S еще заметно не расширяются, в то время как уровень 3S сильно расширен. Еще большему расширению подвергаются уровни ЗР, 3d и т.д., соответствующие возбужденным состояниям атома. Расширение уровней 3S и 3Р настолько велико, что они перекрываются.
Если энергетический уровень в изолированном атоме имеет (2l + 1) – кратное вырождение, то соответствующая ему энергетическая зона в кристалле будет состоять из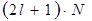 
подуровней, где N- число атомов в кристалле. Снятие вырождения связано с взаимодействием атомов при их сближении на характерное для кристалла расстояние d. Расстояние между уровнями в зоне очень мало. Например, в кристалле размером 1 см3 содержится 
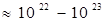атомов. При ширине зоны порядка 1 эВ расстояние между уровнями в ней равно » 10-22 ¸ 10-23 эВ. На рис. 5.3 видно, что энергетические зоны, в которых имеются разрешенные значения энергии для электронов, отделены друг от друга зонами запрещенных энергий.
Для изображения энергетических зон кристалла обычно пользуются упрощенной энергетической схемой (рис.5.4).
Так как электрические, оптические и другие свойства кристаллов объясняются состоянием валентных электронов, то на схеме изображают только две разрешенные энергетические зоны: валентную зону, соответствующую нормальным (невозбужденным) состоянием валентных электронов, и ближайшую к ней зону проводимости (зону возбужденных состояний). Эта зона называется зоной проводимости потому, что в отсутствие внешних возбуждений в ней нет электронов, а при получении необходимой энергии (порядка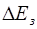 
) в эту зону переходит электрон из валентной зоны и сможет двигаясь под действием внешнего электрического поля изменять свою энергию.
Дата добавления: 2015-07-24; просмотров: 1422;