ДВИЖЕНИЕ ЭЛЕКТРОНА В КРИСТАЛЛЕ ПОД ДЕЙСТВИЕМ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ЭФФЕКТИВНАЯ МАССА.

Движение электрона в периодическом потенциальном поле кристалла описывается волновым пакетом составленным из плоских волн с близкими значениями волнового числа k. Групповая скорость волнового пакета отождествляется со скоростью движения электрона.

Из определения групповой скорости

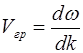, (5.14)

где 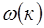– частота волны как функция к, и соотношения 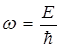, находим

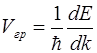. (5.15)

Ускорение электрона в кристалле найдем продифференцировав выражение (5.15) по t:

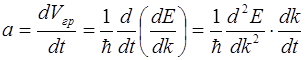. (5.16)

Учитывая корпускулярно-волновое соотношение 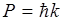и дифференцируя его по t получим:

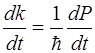. (5.17)

Если кристалл помещен в электрическое поле, то изменение импульса электрона равно действующей на него силе

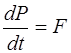. (5.18)

Подставив (5.17) и (5.18) в (5.16), получим

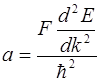. (5.19)

Из сравнения выражения (5.19) с уравнением второго закона Ньютона следует, что роль массы по отношению к внешней силе играет величина

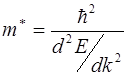. (5.20)

Величина m* - получила название эффективной массы. Из-за взаимодействия электрона с кристаллической решеткой эффективная масса может существенно отличаться от массы свободного электрона.

С учетом внешней силы 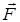и силы действующей на электрон в кристалле 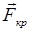уравнение второго закона Ньютона можно записать в виде:

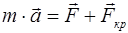. (5.21)

Если выражение (5.20) подставить в формулу (5.19), то получим

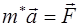. (5.22)

Сравнивая уравнения (5.21) и (5.22) приходим к заключению, что действие силы учитывается эквивалентным образом за счет введения вместо массы свободного электрона эффективной массы.

В соответствии с формулой (5.20) изменения эффективной массы определяется изменением 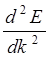. График функции E(k) для первой зоны Бриллюэна представлен на рис. 5.9.

У электрона, находящегося в нижней части зоны (точка А на рис. 5.9, а) эффективная масса 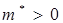, так как . Зависимость E(k) на участке ОА не отличается от параболы, поэтому скорость электрона под действием внешней силы растет, а эффективная масса приблизительно равна массе свободного электрона (рис. 5.9 б).

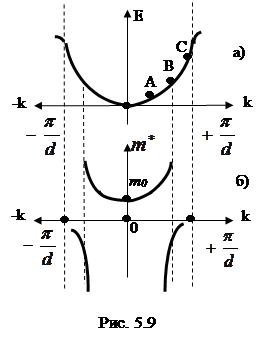В точке перегиба (точка В на рис. 5.9, а) 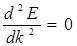и, следовательно, в соответствии с формулой (5.20) 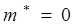. Это означает, что в точке В действие силы компенсируется силой 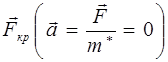. При дальнейшем увеличении волнового вектора (точка С на рис. 5.9 а) электрона под действием внешнего электрического поля того же направления скорость электрона уменьшается, так как он получает отрицательное ускорение 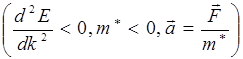; направленное противоположно силе .

Покажем, что поведение электронов в верхней части зоны где их эффективная масса 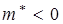, можно описать с помощью частиц с положительным зарядом +е, положительной эффективной массой .

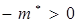Уравнение движение электрона во внешнем электрическом поле с напряженностью 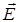имеет вид:

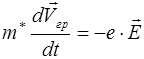. (5.23)

Перенесем знак минус из первой части уравнения в левую, тогда получим эквивалентное уравнение

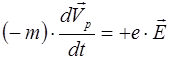. (5.24)

Учитывая, что -m^*>0 действительно убеждаемся в возможности замены при описании поведения электрона в верхней части зоны частицей с положительной массой и положительным зарядом. Такую частицу принято называть дыркой.

Если в верхней части зоны имеются вакантные состояния их отождествляют с дырками, так как отсутствие электрона на вакантном уровне, эквивалентно наличию на нем положительно заряженной частицы (+e) с положительной эффективной массой -m^*>0.

Движение дырки не связано с движением реальной положительно заряженной частицы. По кристаллу движется электрон, переходя от одного атома к другому на «свободное» место.

Само свободное место (дырка), очевидно перемещается в противоположном направлении. Перенос заряда, связанный с перемещением дырок под действием электрического поля лежит в основе так называемой дырочной проводимости.

В заключение отметим, что эффективная масса электрона в кристалле не определяет его инерционные и гравитационные свойства. Введение этой величины дает возможность, учитывая сложный характер взаимодействия электрона с решеткой при его движении под действием внешнего электрического поля, пользоваться простыми формулами движение электрона в нижней части энергетической зоны:

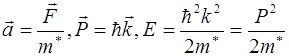(5.25)