ПОНЯТИЕ О КВАНТОВОЙ ТЕОРИИ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ И СВЕРХПРОВОДИМОСТИ
Расчет удельной электропроводности металлов, основанный на квантовой теории металлов, был выполнен Зоммерфельдом. Для удельной электропроводности им получено следующее выражение:
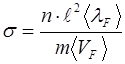 , (6.21)
, (6.21)
которое по внешнему виду напоминает формулу для σ в классической теории электропроводности металлов (часть II Курса физики для ВВУЗов связи МО РФ). В классической теории 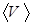 является средней скоростью теплового движения свободных электронов, пропорциональной
является средней скоростью теплового движения свободных электронов, пропорциональной 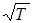 .
.
В формуле (6.21) 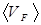 средняя скорость теплового движения электрона, имеющего энергию равную энергии Ферми. Так как энергия Ферми практически не зависит от температуры, то
средняя скорость теплового движения электрона, имеющего энергию равную энергии Ферми. Так как энергия Ферми практически не зависит от температуры, то 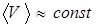 (Т). Основное отличие формулы (6.21) от классической состоит в истолковании величин
(Т). Основное отличие формулы (6.21) от классической состоит в истолковании величин 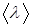 и
и 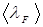 . Согласно классической теории
. Согласно классической теории 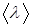 - средняя длина свободного пробега электрона при его столкновениях с атомными остатками, равная периоду кристаллической решетки. В квантовой теории движение электронов проводимости в металле описывается распространением волн де Бройля. Механизм распространения волн де Бройля напоминает механизм рассеяния оптической волны в мутных средах.
- средняя длина свободного пробега электрона при его столкновениях с атомными остатками, равная периоду кристаллической решетки. В квантовой теории движение электронов проводимости в металле описывается распространением волн де Бройля. Механизм распространения волн де Бройля напоминает механизм рассеяния оптической волны в мутных средах.
Рассеяние света возникает если центры рассеяния расположены в среде на расстояниях не меньших длины волны  . Если же
. Если же 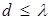 , то рассеяние не наблюдается. Аналогичное явление происходит при распространении электронных волн в металле. Идеальная кристаллическая решетка с неподвижными ионами не рассеивает электронные волны и не оказывает электрическому току никакого сопротивления. Рассеяние электронных волн и связанное с ним сопротивление проводника возникают, если в кристаллической решетке существуют центры рассеяния – искажения упорядоченности решетки, размеры которых d превосходят длину волны де Бройля электронов. В кристаллической решетке реального металла всегда имеются искажения в виде примесей чужеродных атомов, и тепловых колебаний.
, то рассеяние не наблюдается. Аналогичное явление происходит при распространении электронных волн в металле. Идеальная кристаллическая решетка с неподвижными ионами не рассеивает электронные волны и не оказывает электрическому току никакого сопротивления. Рассеяние электронных волн и связанное с ним сопротивление проводника возникают, если в кристаллической решетке существуют центры рассеяния – искажения упорядоченности решетки, размеры которых d превосходят длину волны де Бройля электронов. В кристаллической решетке реального металла всегда имеются искажения в виде примесей чужеродных атомов, и тепловых колебаний.
Рассеивающая способность кристаллом электронных волн, обусловленная флуктуациями плотности за счет тепловых колебаний решетки, оценивается коэффициентом рассеяния 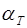 . Коэффициент рассеивания связан с длиной свободного пробега электрона и характеристиками теплового движения ионов в узлах решетки, что позволяет получить выражение:
. Коэффициент рассеивания связан с длиной свободного пробега электрона и характеристиками теплового движения ионов в узлах решетки, что позволяет получить выражение:
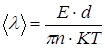 , (6.22)
, (6.22)
где n - число атомов в единице объема, E - модуль упругости, d параметр решетки.
Подставив 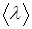 из (6.22) в формулу (6.21) тогда получим:
из (6.22) в формулу (6.21) тогда получим:
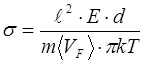 (6.23)
(6.23)
Из (6.23) следует, что удельное сопротивление 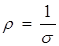 прямо пропорционально Т, что находится в хорошем согласии с опытом при комнатных температурах.
прямо пропорционально Т, что находится в хорошем согласии с опытом при комнатных температурах.
Например, для серебра при Е=107 Па, d = 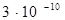 м, m =9,1∙10-31 кг,
м, m =9,1∙10-31 кг,
КТ =4,2∙10-21 Дж (комнатная температура) и 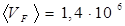 м/с. Формула (6.23) дает σ =5∙107 Ом-1∙м-1. Из опыта получается близкое значение: σ = 6,3∙107 Ом-1 м-1. При низких температурах формулы (6.22) и (6.23) не справедливы.
м/с. Формула (6.23) дает σ =5∙107 Ом-1∙м-1. Из опыта получается близкое значение: σ = 6,3∙107 Ом-1 м-1. При низких температурах формулы (6.22) и (6.23) не справедливы.
С учетом наличия примесей коэффициент рассеивания электронных волн состоит из двух вкладов:
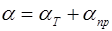 (6.24)
(6.24)
Для не слишком низких температур αт пропорционален Т, а αпр пропорционален концентрации примесей и не зависит от температуры. В соответствии с этим удельное сопротивление металла можно представить в виде:
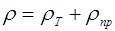 (6.25)
(6.25)
При Т → 0 ρт → 0 и ρ→ρпр, не зависящей от температуры (остаточное удельное сопротивление). Чем химически чище металл и чем меньше в нем различных неоднородностей, обусловленных внутренними напряжениями, тем меньше его остаточное удельное сопротивление.
Характер зависимости удельного сопротивления металлического проводника от температуры представлен на рис.6.5.
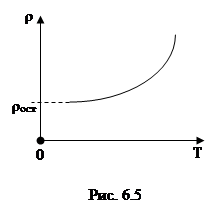 В 1911 г. Х.Камерлинг-Оннес провел экспериментальное исследование удельного сопротивления чистой ртути при низких температурах. Замкнутый проводник из твердой ртути помещался между полюсами электромагнита. При выключении тока в обмотке электромагнита в проводнике возникал индукционный ток, который весьма быстро затухал. При охлаждении ртути жидким гелием до температуры Т ≈ 4,15 К сопротивление ртути резко уменьшалось и индукционный ток продолжал течь по проводнику в течении многих часов без заметного ослабления. Это явление получило название сверхпроводимости, а вещества, обладающие таким свойством, были названы сверхпроводниками. Явление сверхпроводимости обнаружено еще у 22 металлов (свинец, цинк, алюминий и другие) и большого числа сплавов.
В 1911 г. Х.Камерлинг-Оннес провел экспериментальное исследование удельного сопротивления чистой ртути при низких температурах. Замкнутый проводник из твердой ртути помещался между полюсами электромагнита. При выключении тока в обмотке электромагнита в проводнике возникал индукционный ток, который весьма быстро затухал. При охлаждении ртути жидким гелием до температуры Т ≈ 4,15 К сопротивление ртути резко уменьшалось и индукционный ток продолжал течь по проводнику в течении многих часов без заметного ослабления. Это явление получило название сверхпроводимости, а вещества, обладающие таким свойством, были названы сверхпроводниками. Явление сверхпроводимости обнаружено еще у 22 металлов (свинец, цинк, алюминий и другие) и большого числа сплавов.
 Температурная зависимость сопротивления сверхпроводников имеет вид, представленный на рис. 6.6.
Температурная зависимость сопротивления сверхпроводников имеет вид, представленный на рис. 6.6.
Переходной области АВ соответствует небольшой температурный интервал, величина которого зависит от наличия примесей и внутренних напряжений. Для химически чистых образцов он не превышает тысячных долей градуса. Температуру перехода в сверхпроводящее состояние называют критической температурой Ткр.
При заметной ширине области АВ за критическую температуру принимают температуру, при которой сопротивление равно 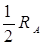 (рис. 6.6). Удельное сопротивление сверхпроводника меньше 10-23 Ом∙см, что по сравнению с удельным сопротивлением меди, которое равно 10-9 Ом∙см, составляет ничтожно малую величину. Отсутствие сопротивления у сверхпроводника является важнейшим, но не единственным свойством. У них наблюдается особые магнитные и другие свойства.
(рис. 6.6). Удельное сопротивление сверхпроводника меньше 10-23 Ом∙см, что по сравнению с удельным сопротивлением меди, которое равно 10-9 Ом∙см, составляет ничтожно малую величину. Отсутствие сопротивления у сверхпроводника является важнейшим, но не единственным свойством. У них наблюдается особые магнитные и другие свойства.
В 1933 г. В. Мейснером и Р. Оксенфельдом экспериментально открыт эффект “выталкивания магнитного поля из объема сверхпроводника”. Магнитное поле не проникает в объем сверхпроводника, если индукция не превышает некоторого критического значения Вк (Т), зависящего от температуры и характерного для данного материала (рис. 6.7).

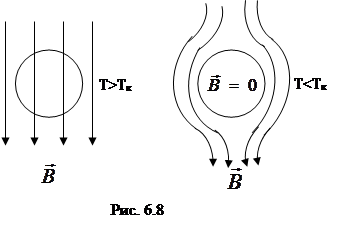 |
Если поместить металл в нормальном состоянии в магнитное поле В < Вк, и затем снижать температуру, то в момент перехода металла в сверхпроводящее состояние магнитное поле выталкивается из объема
(рис. 6.8)
Более детальные исследования показали, что магнитное поле в тонком поверхностном слое толщиной 10-5 – 10-6 см уменьшается от значения на поверхности до нуля. Эффект Мейснера связан с тем, что при переходе в сверхпроводящее состояние, например, цилиндрического образца в магнитном поле В <Вк, в поверхностном слое толщиной 10-5 – 10-6 см, возникает незатухающий круговой ток, такой силы, что его магнитное поле 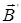 компенсирует внешнее магнитное поле
компенсирует внешнее магнитное поле 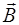 в толще сверхпроводника (рис. 6.9).
в толще сверхпроводника (рис. 6.9).
 В создании современной теории сверхпроводимости существенную роль сыграло открытие в 1950 г. изотопического эффекта. Для изотопов ртути была установлена связь между критической температурой и массовым числом М;
В создании современной теории сверхпроводимости существенную роль сыграло открытие в 1950 г. изотопического эффекта. Для изотопов ртути была установлена связь между критической температурой и массовым числом М;
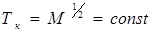 (6.26)
(6.26)
Масса изотопа является характеристикой кристаллической решетки, так как основной вклад в нее вносят ионы металла. С другой стороны, многочисленные экспериментальные факты свидетельствуют о том, что сверхпроводимость – свойство электронной системы сверхпроводника. Идея, лежащая в основе теории сверхпроводимости, состоит в том, что возникновение сверхпроводящего состояния обусловлено особым взаимодействием электронов с решеткой.
Последовательная микроскопическая теория сверхпроводимости была создана в 1957 году Дж.Бардиным, Л.Купером, Дж. Шрифером и Н.Боголюбовым. Физическая сущность этой теории состоит в следующем.
Свободные электроны металла образуют электронный газ, подчиняющийся статистике Ферми-Дирака. Между электронами действуют кулоновские силы отталкивания, которые в значительной степени ослаблены наличием поля положительных ионов, расположенных в узлах решетки. Кроме того, электроны взаимодействуют с тепловыми колебаниями решетки. Основной вклад в энергию тепловых колебаний решетки, как показало П.Дебай, вносят колебания низких частот, соответствующих упругим волнам. В кристалле упругие волны имеют квантовые свойства, проявляющиеся в том, что существует наименьшая порция (квант) энергии волны с данной частотой ν. Это позволяет сопоставить волне с частотой ν квазичастицы – фононы, распространению которых соответствует упругая волна.
Причиной электрического сопротивления металла в нормальном состоянии является электрон – фононное взаимодействие, которое разупорядочивает движение электронов.
При низких температурах электрон-фононное взаимодействие может привести к некоторому эффективному притяжению между электронами, механизм которого состоит в следующем. Электрон, взаимодействуя с кристаллической решеткой переводит ее в возбужденное состояние (возбуждает фонон) и изменяет свой импульс. Энергия возбуждения (фонон) передается другому электрону, который тоже изменяет свой импульс. В результате состояние решетки не изменяется, а между электронами может возникнуть связанное состояние – куперовская пара. Куперовские пары возникают в случае, когда притяжение электронов преобладает над кулоновским отталкиванием. Расчет показывает, что этому условию удовлетворяют электроны, у которых энергия близка к энергии Ферми, импульсы равны и противоположно направлены, а спины антипараллельны.
Размеры области, в которой локализованы электроны, образующие куперовскую пару, значительно превышают межатомное расстояние. Это означает, что между электронами, связанными в пару находится достаточно много несвязанных электронов.
Куперовские пары обладают нулевым спином и поэтому не описываются статистикой Ферми-Дирака. Частицы с целым спином описываются статистикой Бозе-Эйнштейна и называются бозонами. Число бозонов, находящихся в одном квантовом состоянии не ограничено. Поэтому при температуре меньше критической подавляющее число пар будет находится в основном состоянии, из которого их довольно сложно перевести в возбужденное. Энергия связи электронов в паре очень мала (~3.5 кТкр), однако отрыву электрона препятствует коллектив взаимодействующих друг с другом пар электронов. Пары беспрерывно обмениваются друг с другом электронами, поэтому все электроны в системе связаны.
Энергетический спектр такой электронной системы характеризуется тем, что возбужденное состояние отделено от основного некоторым интервалом энергии – энергетической щелью, внутри которой нет разрешенных уровней. Ширина щели определяет энергию разрыва пары. Квантовые переходы электронной системы не происходят при Т < Ткр. При включении электрического поля весь коллектив электронов смещается в металле как целое, то есть создает электрический ток. Чтобы возникло сопротивление, необходимо перебросить электроны на энергетические уровни выше щели. При повышении температуры Т>Ткр (или увеличении тока до I>Iкр) растет число распавшихся пар и сверхпроводящее состояние разрушается.
На основе теории сверхпроводимости английский физик Б. Джозефсон в 1962 году предсказал эффект, названный его именем. Эффект Джозефсона состоит в протекании сверхпроводящего туннельного тока через слой изолятора, разделяющий два сверхпроводника (джозефсоновский контакт). Для протекания туннельного сверхпроводящего тока слой диэлектрика должен иметь толщину ≈ 10-9 м.
Если металлы находятся в несверхпроводящем состоянии, то ток через контакт осуществляется за счет туннелирования неспаренных электронов - нормальный ток. Если же металлы находятся в свехпроводящем состоянии, то через контакт, кроме нормального тока течет сверхпроводящий ток, обусловленный туннелированием куперовских пар через слой диэлектрика. Если сверхпроводящий ток через джозефсоновский контакт не превышает определенного значения, называемого критическим током контакта, то падение напряжения на контакте равно нулю. Описанный эффект называется стационарным эффектом Джозефсона.
Если же через контакт течет ток больше критического, то напряжение на нем становится отличным от нуля и он испускает фотон.
Поскольку электромагнитные волны может излучать только переменный ток, то в этом случае через контакт Джозефсона течет переменный ток при постоянном напряжении. Циклическая частота переменного тока равна частоте порожденного им электромагнитного излучения. Описанный эффект называется нестационарным эффектом Джозефсона.
Эффект Джозефсона используется для точного измерения очень слабых магнитных полей (до 10-18 Тл), токов (до 10-10 А) и напряжений (до 10-15 В), а также для создания быстродействующих элементов логических устройств ЭВМ.
Дата добавления: 2015-07-24; просмотров: 2345;
