РАВНОВЕСНЫЕ КОНЦЕНТРАЦИИ СВОБОДНЫХ НОСИТЕЛЕЙ И ПОЛОЖЕНИЕ УРОВНЯ ФЕРМИ В ПОЛУПРОВОДНИКЕ

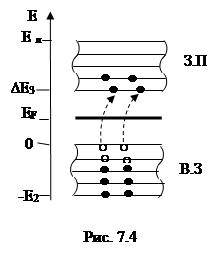
Рассчитаем сначала концентрации свободных электронов n₀ и дырок P₀ в собственном полупроводнике. Воспользуемся результатами, полученными в §6.1. В собственном полупроводнике свободные электроны расположены на нижних уровнях зоны проводимости, а дырки – на верхних уровнях валентной зоны (рис.7.4).

Вероятность заполнения электроном уровня с энергией Е определяется функцией Ферми-Дирака

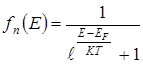(7.6)

Вероятность заполнения энергетического уровня Е вблизи валентной зоны дыркой можно рассматривать как вероятность того, что энергетический уровень не занят электроном, то есть

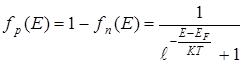(7.7)

Так как значения функций (7.6) и (7.7) зависят от разности E-E_F , то E и E_F необходимо отсчитывать от одного начала отсчета энергии. Примем за начало отсчета энергии потолок валентной зоны (рис.7.4).

Концентрации свободных электронов в зоне проводимости и дырок в валентной зоне в соответствии с формулой (6.9) определяются выражениями.

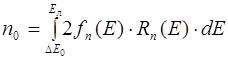, (7.8)

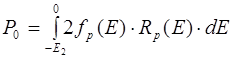. (7.9)

С учетом выбора начала отсчета энергии, функции плотности уровней энергии в единице объема полупроводника (6.6) принимают вид:

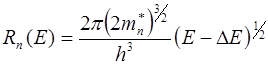; (7.10)

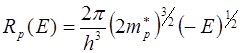. (7.11)

Вероятности заполнения электронами уровней зоны проводимости и дырками уровней валентной зоны малы, так как ∆E₃ >> кт. Поэтому f_p<<1 и f_n<<1 и, следовательно, функции (7.6) и (7.7) можно записать в виде:

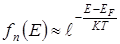; (7.12)

. (7.13)

Отметим, что функции (7.6) и (7.7) переходят в функции (7.12), (7.13), если

E-E_F> 3 K.Т.

Полученные функции представляют собой функции распределения Максвелла-Больцмана (6.14). Таким образом, в случае небольших концентраций электронов и дырок электронный и дырочный газы в полупроводнике являются невырожденными, то есть их свойства подобны свойствам классического идеального газа.

Подставив выражения (7.10) и (7.12) в формулу (7.8) получим:

. (7.14)

Сделаем (7.14) замену ε = E -∆E и учтем, что вероятность заполнения электронами верхних уровней зоны проводимости практически равна нулю. Верхний предел интегрирования при этом ε₁=E₁ -∆E можно заменить на ∞. После выполнения интегрирования в (7.14), находим равновесную концентрацию электронов в зоне проводимости.

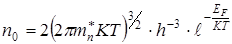(7.15)

Подставив выражения (7.11) и (7.13) в формулу (7.9) получим:

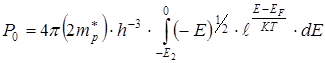. (7.16)

Сделаем в (7.16) замену и учтем, что вероятность заполнения дырками уровней вблизи дна валентной зоны практически равна нулю (при этом можно вместо –E₂ взять -∞). После выполнения интегрирования в (7.16), получим

. (7.17)

В собственном полупроводнике свободные электроны и дырки возникают парами, поэтому n₀ = P₀. Приравняв правые части выражения (7.15) и (7.17) и, выполнив несложные преобразования, для энергии Ферми найдем выражение:

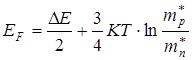(7.18)

Из выражения (7.18) следует, что при Т=ОК уровень Ферми в собственном полупроводнике расположен посредине запрещенной зоны (рис.7.4). Как правило 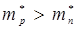, поэтому с ростом температуры уровень Ферми смещается ближе к дну зоны проводимости.

Подставим найденное для E_F выражение (7.18) в выражения (7.15) и (7.17), тогда получим

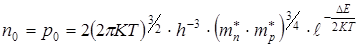. (7.19)

В примесном полупроводнике, если концентрация электронов в зоне проводимости мала, то f_n(E) << 1 и, следовательно, она может быть вычислена так же, как n₀ для собственного полупроводника:

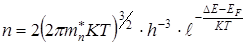. (7.20)

Аналогично, в случае малой концентрации дырок в валентной зоне примесного полупроводника f_p(E) <<1, и, следовательно, она вычисляется как р₀ для собственного полупроводника:

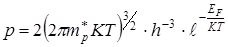(7.21)

Перемножим выражения (7.20) и (7.21) и возведем выражение (7.19) в квадрат, тогда получим:

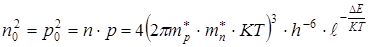(7.22)

Таким образом, из (7.22) следует равенство:

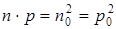(7.23)

Равенство (7.23) выражает закон действующих масс, который называют так по аналогии с законом действующих масс в химии. Равновесные концентрации электронов и дырок в любом невырожденном полупроводнике, как следует из равенства (7.23), таковы, что их произведение равно квадрату концентрации электронов или дырок в собственном полупроводнике.

Равенство (7.23) справедливо при любой температуре, поэтому при Т ≠ ОК всегда имеются как равновесные свободные электроны, так и равновесные свободные дырки, причем произведение их концентрации отлично от нуля и равно 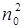(или ).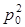

Равновесные концентрации электронов и дырок в примесных полупроводниках, как следует из выражений (7.20) и (7.21) зависят от положения уровня Ферми. Положение уровня Ферми в примесных полупроводниках не может быть найдено также просто как в собственных, поскольку n ≠P.

На рис. 7.5 представлены температурные зависимости положения уровня Ферми в донорном (рис. 7.5 а) и акцепторном (рис. 7.5 б) полупроводниках.

При абсолютном нуле температуры уровень Ферми располагается посредине между примесными уровнями и дном зоны проводимости – для донорных полупроводников, примесными уровнями и потолком валентной зоны – для акцепторных полупроводников. С повышением температуры уровень Ферми сначала смещается к ближайшей разрешенной зоне и при температурах, при которых примесные атомы полностью ионизуются и увеличение концентрации носителей происходит только за счет возбуждения собственных носителей, он располагается посредине запрещенной зоны, как в собственном полупроводнике.

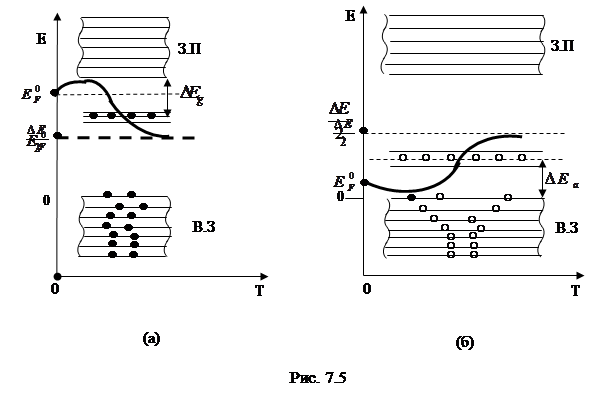Если температура примесного полупроводника сравнительно низкая и примесные атомы ионизированы только частично, то соответствующий расчет приводит к следующим выражениям для концентраций основных носителей:

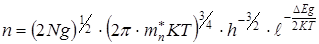; (7.24)

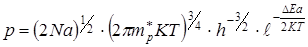(7.25)

где N_g и N_a - концентрации атомов доноров и акцепторов, соответственно.

В случае достаточно высоких температур, когда примесные уровни полностью ионизированы (примесное истощение), а концентрация собственных носителей еще невелика (n₀ << N_g, р₀ << Na) расчет приводит к следующему результату:

(7.26)

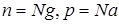<10111213141516>

---

Дата добавления: 2015-07-24; просмотров: 1464;

---