ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ

Удельная электропроводность полупроводника определяется концентрацией свободных носителей заряда и их подвижностями:

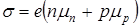(7.27)

Концентрации свободных электронов и дырок в собственных и примесных полупроводниках описываются выражениями (7.19), (7.24), (7.25).

Подвижности свободных носителей определяются характером рассеяния электронных волн на дефектах кристаллов, к которым относятся примесные атомы, дислокации, границы зерен, дефекты по Френкелю и Шоттки, тепловые колебания решетки.

В атомных полупроводниках при больших температурах преобладает рассеяние на тепловых колебаниях, при низких температурах преобладает рассеяние на примесях.

Если в рассеянии носителей участвуют оба механизма, то полагая, что их действие является независимым и аддитивным величину обратную подвижности можно представить в виде:

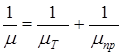(7.28)

где μ_т - подвижность носителей в условиях, когда основное значение имеет рассеяние на тепловых колебаниях решетки; μ_пр - подвижность носителей, когда преобладает механизм рассеяния на ионизированных примесях.

Соответствующий теоретический расчет дает следующую зависимость величины обратной подвижности от температуры:

(7.29)

При низких температурах преобладает первое слагаемое, при высоких – второе.

Зависимость (7.29) в полулогарифмической системе координат представлена на

рис. 7.6 для высоких (1) и низких температур (2).

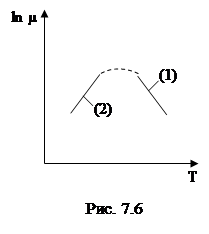Положение максимума смещается в область более высоких температур с ростом концентрации дефектов.

Из сравнения выражений (7.19), (7.24), (7.25) с выражением (7.29), следует, что температурная зависимость удельной электропроводности полупроводника (7.27) в основном определяется зависимостью от температуры концентрации носителей и может быть представлена выражением:

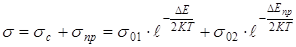, (7.30)

где σ_c и σ_пр - удельные электропроводности, созданные собственными и примесными носителями, σ₀₁ и σ₀₂ - коэффициенты, слабо зависящие от температуры.

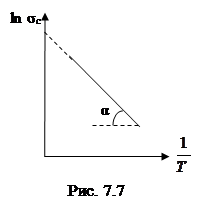Для собственных полупроводников в выражении (7.30) второе слагаемое в правой части отсутствует. Зависимость σ_с от температуры удобно представить в полулогарифмических координатах:

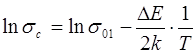. (7.31)

Из формулы (7.31) следует, что для собственных полупроводников логарифм удельной электропроводности, пренебрегая слабой температурой зависимостью lnσ₀₁, можно считать линейной функцией от 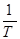(рис. 7.7).

Тангенс угла наклона этой прямой к оси абсцисс равен 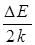, а отрезок, отсекаемый продолжением прямой на оси ординат ln σ₀₁. Экспериментальные исследования зависимости удельной электропроводности собственных полупроводников от температуры находятся в хорошем согласии теоретической зависимостью, приведенной на рис. 7.7.

Для примесного полупроводника в области комнатных (низких) температур определяющим в выражении (7.30) является второе слагаемое, а в области высоких температур, когда наступает примесное истощение – первое. Зависимость удельной электропроводности примесных полупроводников от температуры, также как для собственных полупроводников, удобно представлять в полулогарифмических координатах:

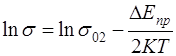- для низких Т, (7.32)

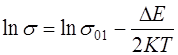- для высоких Т. (7.33)

Зависимость логарифма удельной электропроводности примесного полупроводника от температуры имеет вид поломанной линии, в соответствии с преимущественным вкладом собственных и примесных носителей заряда (рис. 7.8).

В области низких температур в полупроводнике преобладает примесная проводимость (участки 1-2, 1′ – 2′), возрастание которой определяется увеличением концентрации примесных носителей заряда с ростом температуры. Участки 2-3, 2′ – 3′) соответствуют температурам, при которых наступает примесное истощение, а собственная электропроводность еще очень мала.

Спад электропроводности с ростом температуры на этих участках связан с уменьшением подвижности носителей заряда (рис. 7.6).

При дальнейшем возрастании температуры преобладающей становится собственная электропроводность, которая быстро увеличивается с ростом температуры (линия АВ на рис. 7.8) за счет возрастания концентрации собственных носителей. При увеличении концентрации примесных атомов ( 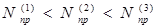) в полупроводнике, участки ломаной линии 1-2-3 смещаются вверх по оси ординат в положение 1′ – 2′ – 3′, а температура перехода от примесной электропроводности к собственной смещается в область более высоких температур. При больших концентрациях примеси примесное истощение не наступает вплоть до температур, при которых преобладающей становится собственная электропроводность. Спад электропроводности при этом не наблюдается (участок 1′′ – 3′′ на рис. 7.8). Как следует из выражений (7.32), (7.33) и рис. 7.8 по тангенсам углов α₁ и α₂ можно определить ширину запрещенной зоны и энергию активации примесей.