В ПОЛУПРОВОДНИКЕ

В 1879 г. Холл открыл эффект, который состоит в следующем. Пусть по проводнику, имеющему форму прямоугольного параллелепипеда (рис. 7.9), протекает электрический ток.

На параллельных плоскости листа гранях параллелепипеда всегда можно выбрать точки А и D, лежащие на одной эквипотенциальной поверхности. Напряжение между этими точками U_x = 0. Если включить магнитное поле перпендикулярно току, так как показано на рис. 7.9 а, то между точками A и D возникает напряжение Холла U_x ≠ 0.

Как показывает опыт, при не слишком сильных полях напряжение Холла пропорционально индукции магнитного поля, плотности тока и ширине пластины:

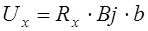, (7.34)

где R_x является константой материала и называется постоянной Холла.

Рассмотрим физическую природу эффекта Холла. При движении электронов в проводнике (рис. 7.9 а) на них действует сила Лоренца, заставляя их смещаться к передней грани пластины. В следствии этого передняя грань заряжается отрицательно, а задняя – объединится электронами – положительно. В пластине появится поперечное электрическое поле E_x. Смещение электронов будет продолжаться до тех пор, пока сила Лоренца не уравновесится силой поперечного электрического поля, действующей на электроны в направлении, противоположном силе Лоренца, то есть

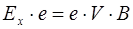(7.35)

Учтем, что плотность тока j = e∙n∙v и 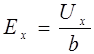, тогда после несложных преобразований получим

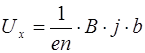(7.36)

Из сравнения формулы (7.36) с формулой (7.34) следует, что для металлического проводника постоянная Холла равна

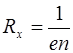. (7.37)

Описанный вывод не является строгим, так как он предполагает, что все электроны проводимости имеют одну и ту же скорость теплового движения, вследствие чего время свободного движения между двумя последовательными взаимодействиями с центрами рассеивания принимается у всех электронов одинаковым. В этом случае под действием внешнего электрического поля все электроны приобретают одинаковую скорость дрейфа. Такое приближение оказывается справедливым для металлов и сильно легированных полупроводников, проводимость которых обеспечивается только электронами, располагающимися на уровнях вблизи уровня Ферми и обладающих практически одинаковыми скоростями. В общем случае необходимо учитывать распределение носителей заряда по скоростям. Более строгий расчет учитывающий распределение носителей по скоростям приводит для постоянной Холла к выражению:

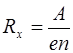. (7.38)

Для полупроводников, имеющих решетку типа алмаза (Ge, Si, JnSb, AlAs и др) и носители одного знака,

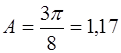, (7.39)

если основным является механизм рассеяния носителей на тепловых колебаниях решетки, и

,

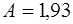(7.40)

если основным является механизм рассеяния на ионизированных атомах примеси.

Для полупроводников со смешанной проводимостью (электронной и дырочной)

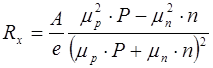, (7.41)

где А – так же, как и в случае носителей одного знака, определяется механизмом рассеяния.

Для собственных полупроводников, в которых n₀ =P₀, формула (7.41) переходит в следующую:

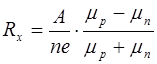^. (7.42)

В случае полупроводника с одним типом проводимости, определив из опыта постоянную Холла, можно найти по формуле (7.38) концентрацию носителей заряда. Если известно значение удельной электропроводности 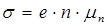, то можно рассчитать подвижность носителей по формуле

(7.43)

Нетрудно заметить (рис. 7.9 а, б), что по знаку холловской разности потенциалов можно определить знак носителей заряда в полупроводнике. Эффект Холла используется для измерения индукции магнитных полей, токов высоких частот, в электронных преобразователях, усилителях и генераторах электрических колебаний.