УРАВНЕНИЕ НЕПРЕРЫВНОСТИ ДЛЯ ПОЛУПРОВОДНИКА
Уравнение непрерывности для проводника отражает закон сохранения заряда
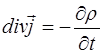 , (7.71)
, (7.71)
где ρ - объемная плотность электрического заряда в рассматриваемой точке.
Если заряд не накапливается и не расходуется, то есть сохраняется, то 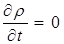
и уравнение (7.71) принимает вид:
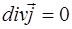 (7.72)
(7.72)
Математически уравнение (7.72) отражает отсутствие в рассматриваемой точке источников и стоков электрических зарядов.
 В отличие от проводников, в полупроводниках могут протекать процессы генерации и рекомбинации носителей заряда. Получим уравнение непрерывности для полупроводника. Смысл этого уравнения должен состоять в том, что в стационарном состоянии число носителей, выходящих из некоторого объема полупроводника, равно числу носителей входящих в него и созданных в нем за счет генерации за вычетом числа рекомбинированных носителей. Рассмотрим простейший случай, когда направленная концентрация неосновных носителей заряда (например, электронов в полупроводнике р-типа) изменяется только вдоль оси ОХ (рис. 7.14).
В отличие от проводников, в полупроводниках могут протекать процессы генерации и рекомбинации носителей заряда. Получим уравнение непрерывности для полупроводника. Смысл этого уравнения должен состоять в том, что в стационарном состоянии число носителей, выходящих из некоторого объема полупроводника, равно числу носителей входящих в него и созданных в нем за счет генерации за вычетом числа рекомбинированных носителей. Рассмотрим простейший случай, когда направленная концентрация неосновных носителей заряда (например, электронов в полупроводнике р-типа) изменяется только вдоль оси ОХ (рис. 7.14).
Избыточная над равновесным значением n концентрация неосновных неравновесных носителей заряда равна разности 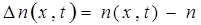 .
.
Число электронов в объеме параллелепипеда равно
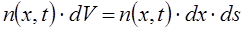 (7.73)
(7.73)
Будем полагать, что генерация носителей заряда, вызванная внешними источниками, в рассматриваемом объеме отсутствует.
Тогда изменение числа электронов в объеме dV будет изменяться за счет различия втекающего и вытекающего токов, а также за счет рекомбинации части электронов с дырками.
Полное изменение числа электронов в объеме dV за время dt можно представить в виде:
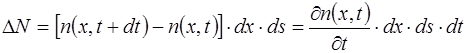 . (7.74)
. (7.74)
Учтем, что изменение заряда в объеме d V за время d t можно выразить через разность плотностей тока на противоположных к нему гранях параллелепипеда
(рис. 7.14).
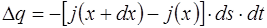 . (7.75)
. (7.75)
Изменение числа электронов в объеме dV за счет различия токов найдем разделив заряд ∆q на заряд электрона e.
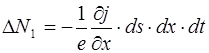 . (7.76)
. (7.76)
Подставив в это выражение формулу (7.62) для плотности электронного тока, получим выражение для ∆N1 в виде:
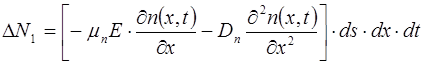 . (7.77)
. (7.77)
В выражении (7.77) считаем напряженность электрического поля E =const (x).
Изменение числа электронов за счет рекомбинации равно со знаком «минус» произведению скорости рекомбинации на объем dV:
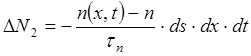 (7.78)
(7.78)
Полное изменение числа электронов в объеме dV, очевидно, равно:
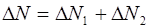 . (7.79)
. (7.79)
Подставив в равенство (7.79) выражения (7.74), (7.77) и (7.78) получим уравнение непрерывности для электронов
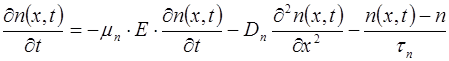 . (7.80)
. (7.80)
Если за счет внешнего источника в полупроводнике протекает процесс генерации со скоростью gn, то уравнение непрерывности принимает вид:
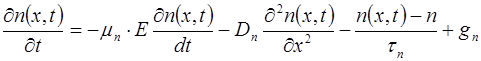 . (7.81)
. (7.81)
Аналогичное уравнение можно получить и для дырок в полупроводнике n-типа:
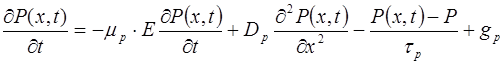 . (7.82)
. (7.82)
Уравнения (7.81) и (7.82) широко используются при анализе процессов протекающих в полупроводниках и полупроводниковых приборах.
Дата добавления: 2015-07-24; просмотров: 2150;
