КВАНТОВАЯ СТАТИСТИКА ЭЛЕКТРОНОВ В МЕТАЛЛЕ.
Электроны в металла обладают волновыми свойствами и их движение описывается уравнением Шредингера. Следствием этого является то, что энергия и другие характеристики движения электрона становятся квантованными, то есть могут принимать лишь строго определенные значения. Каждое значение характеристики движения электрона соответствует определенному квантовому состоянию.
В соответствии с соотношением неопределенностей ( ) два состояния электрона с наборами координат и проекцией импульсов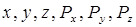 
и 
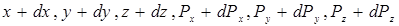неразличимы, если
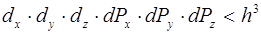(6.1)
В квантовой статистике за элементарную ячейку шестимерного фазового пространства принимается объем, равный
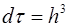(6.2)
При рассмотрении свободных электронов предполагается, что их потенциальная энергия одинакова во всех точках металла, вследствие чего распределение в объеме V является равномерным.
В этом случае вместо шестимерного фазового пространства пользуются трехмерным пространством импульсов Px, Py, Pz и разбивают его на ячейки размером
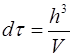(6.3)
Каждый такой ячейке соответствует одно квантовое состояние.
Электроны подчиняются принципу Паули, согласно которому в каждом квантовом состоянии с энергией E, может находиться не более двух электронов, отличающихся направлениями спинов. Это означает, что каждая ячейка в пространстве импульсов объемом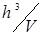 
может вместить не более двух электронов.
Квантовая статистика считает все электроны неотличимыми друг от друга. Поэтому перестановка их местами не приводит к новому состоянию.
Статистический расчет, основанный на отмеченных выше свойствах электронного газа приводит к следующему выражению функции распределения электронов по энергиям:
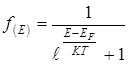(6.4)
где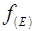 
- вероятность заполнения состояния с энергией E электроном, EF - энергия Ферми (смысл этой величины будет определен ниже). Функция (6.4) называется функцией распределения Ферми-Дирака. Эта функция описывает распределение частиц с полуцелым спином, которые называются фермионами.
Определим число электронов в единице объема, энергия которых заключается в интервале от E до dE. Построим в пространстве импульсов две концентрические сферы с радиусами P и P+dP (рис.6.1). 
Этим сферам соответствуют энергии E и E+dE. Разделим объем шарового слоя между сферами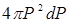 
на объем элементарной ячейки, тогда получим число элементарных ячеек:
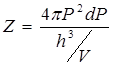(6.5)
Учтем, что для состояний у дна разрешенной зоны (зоны проводимост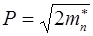и) 
и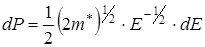 
, тогда для Z получим выражение:
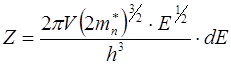(6.5)
Поделив обе части выражения (6.5) на объем металла V и dE определим функцию прочности квантовых уровней Rn (E), то есть число уровней приходящихся в единицу объема металла на единичный интервал энергии:
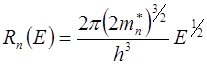(6.6)
Зависимость плотности квантовых уровней от энергии представлена на рис.6.2.
Из выражения (6.6) и рис. 6.2. следует, что квантовые уровни располагаются тем ближе друг к другу, чем больше энергия.
Если в формуле (6.6) вместо эффективной массы электрона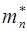 
записать эффективную массу дырки 
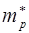, то она будет описывать распределение энергетических уровней в верхней части разрешенной зоны (валентной зоны).
В соответствии с физическим смыслом функции распределения Ферми-Дирака она равна отношению числа электронов в единице объема, имеющих энергию в интервале от E до E+dE к числу квантовых уровней в этом интервале:
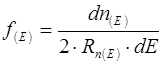, (6.7)
где множитель 2 в знаменателе учитывает принцип Паули.
Из (6.7) находим число электронов в единице объема металла, энергия которых заключена в интервале от E до E+dE:
(6.8)
Для нахождения числа электронов, энергии которых заключены в конечном интервале от E1 до E2, необходимо выражение (6.8) проинтегрировать:
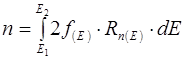(6.9)
Проанализируем функцию Ферми – Дирака (6.4). Если температура металла стремится к абсолютному нулю, то для E>EF функция f(E)→0, для E<EF функция f(E)→1, то есть уровни, расположенные выше уровня Ферми, не заняты электронами (вероятность заполнения равна нулю), а уровни расположенные ниже уровня Ферми обязательно заняты электронами (вероятность заполнения равна единице).
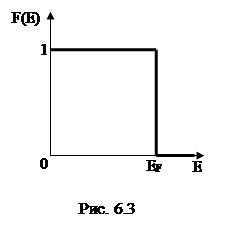На рис. 6.3 представлен график функции f(E) при Т=ОК.
Таким образом, энергия Ферми представляет собой максимальную энергию, которую могут иметь свободные электроны в металле при абсолютном нуле температуры.
Уровень, которому соответствует энергия Ферми, называется уровнем Ферми. Этот уровень отделяет при Т=ОК занятые электронами состояния от незанятых.
Найдем общее число свободных электронов в единице объема металле при Т=ОК. Для этого подставим выражение (6.8) в формулу (6.9) и учтем, что E1 = 0, E2 = EF, f(E) = 1:
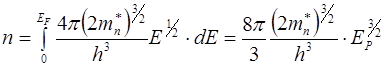(6.10)
Из (6.10) находим для энергии Ферми выражение:
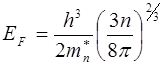(6.11)
Расчет энергии Ферми для характерных значений n и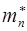 
у металлов дает 
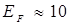эВ.
Вычислим среднюю энергию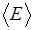 
электрона проводимости при Т=ОК. Для этого рассчитаем суммарную энергию электронов проводимости в единице объема металла:
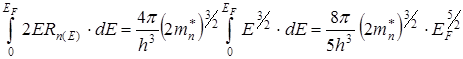
Разделив полученное выражение на общее число электронов (6.10), получим
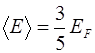(6.12)
Из выражения (6.12) следует, что при абсолютном нуле температуры средняя энергия электронов проводимости в металле не равна нулю. Согласно классической статистике Максвелла - Больцмана при температуре абсолютного нуля средняя кинетическая энергия молекул идеального газа обращается в нуль.
Состояние электронного газа в металлах, характеризуемое резким отличием его свойств от свойств идеального газа называют вырожденным.
Найдем условие при котором вырождение снимается. Если в функции Ферми – Дирака (6.4)
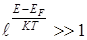, (6.13)
то (6.4), можно записать в виде:
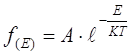, (6.14)
где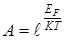 
.
Выражение (6.14) представляет собой функцию Максвелла-Больцмана.
Таким образом, при выполнении условия (6.13) распределение Ферми-Дирака переходит в распределение Максвелла- Больцмана.
Перепишем условие (6.13) в виде:
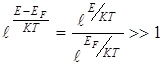(6.15)
Из (6.15) следует, что должно выполняться неравенство
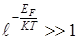(6.16)
Найдем концентрацию электронов проводимости в металлах при соблюдении условия (6.13).
Для этого подставим в формулу (6.9) функцию распределения в виде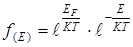 
, 
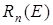из (6.6) и 
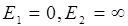(это возможно так как для E>EF f(E)=0), тогда получим:
Интеграл в правой части является табличным.
Он равен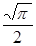 
кг. Таким образом, для n получаем выражение:
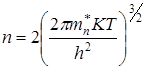(6.17)
откуда находим:
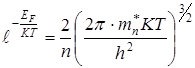(6.17)
С учетом выражения (6.17) условие снятия вырождения (6.16) принимает вид:
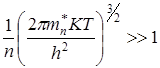(6.18)
При выполнении обратного неравенства
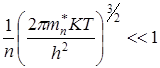(6.19)
электронный газ будет вырожденным.
Из выражения (6.19) следует, что вырождению электронного газа способствует малая эффективная масса электронов, высокая их концентрация и низкая температура. Соответствующий расчет показывает, что во всех металлах электронный газ оказывается вырожденным до температур в несколько тысяч градусов.
Температура TF, при которой вырождение электронного газа в металле снимается, называется температурой Ферми. Грубая оценка величины TF может быть получена, если левую часть выражения (6.18) приравнять к 1. Расчет дает для TF величину порядка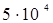 
К.
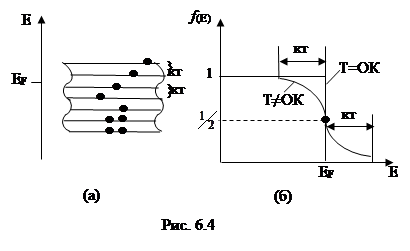Рассмотрим влияние температуры на распределение электронов по энергиям. С повышением температуры тепловому возбуждению могут подвергаться лишь электроны узкой полосы энергий порядка КТ, расположенной вблизи уровня Ферми (рис.6.4а).
Анализ выражения функции Ферми (6.4) при Т ≠ ОК показывает, что если E=EF, то f(E)=1\2, при E>EF f(E)<1\2, а если E<EF, то f(E)>1\2.
Графики функции f(E) при Т = ОК и при Т≠ ОК представлены на рис.6.4,б.
На рисунке видно, что кривые отличаются друг от друга характером спада в области энергий, отличающихся от энергий Ферми на КТ. Это как раз отражает отмеченное выше условие теплового возбуждения электронов. Характер распределения по энергиям электронов располагающихся на более глубоких уровнях, остается таким же, как и при абсолютном нуле температуры. Плавный участок спада в зависимости f(E) для E>EF переходит в кривую Максвелловского распределения, в соответствии с которым распределены электроны по энергиям в узкой полосе энергий порядка КТ. Соответствующий расчет показывает, что изменить свою энергию могут ~1% электронов проводимости металла. Отметим, что с повышением температуры уровень Ферми изменяет свое положение. Для нахождения зависимости EF(Т) найдем общее число свободных электронов в металле проинтегрировав (6.8) в пределах от 0 до ∞:
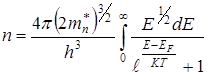
Интегрирование в правой части полученного выражения может быть выполнено приближенно в области низких температур (Т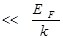 
):
Положив во втором слагаемом в скобках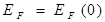 
, найдем
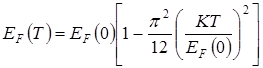(6.20)
Так как вплоть до температуры плавления металла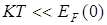 
, зависимость (6.20) очень слабая.
Дата добавления: 2015-07-24; просмотров: 4275;