Влияние температуры на распределение электронов в металле

Для металлов при не слишком высоких температурах выполняется неравенство kT <E это означает, что электронный газ в металлах практически всегда нахо­дится в состоянии сильного вырождения. Температура Т_о вырождения находится из условия kTo = Е . Она опре­деляет границу, выше которой кванто­вые эффекты перестают быть существен­ными. Соответствующие расчеты показы­вают, что для электронов в металле То 10⁴ К, т. е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.

При температурах, отличных от О К, функция распределения Ферми - Дирака плавно изменяется от 1 до 0 в узкой области (порядка kT) в окрестности Е (рис. ). (Здесь же для сравнения пунктиром приведена функция распределе­ния при Т = О К.) Это объясняется тем, что при Т > 0 небольшое число электро­нов с энергией, близкой к Е , возбуж­дается за счет теплового движения и их энергия становится больше Й . Соответ­ственно вблизи границы Ферми при Е < Е среднее число электронов меньше единицы, а при Е > Е — больше нуля. В тепловом движении участвует лишь небольшое число электронов, например при комнатной температуре Т 300 К и температуре вырождения Т = 3-10⁴ К,— это 10^--5 от общего числа электронов.

Если (Е — E_f) » kT («хвост» функции распределения), то единицей в знамена­теле можно пренебречь по срав­нению с экспонентой и тогда распре­деление Ферми - Дирака переходит в рас­пределение Максвелла — Больцмана. Та­ким образом, при (Е — Е) » kT, т.е. при высоких температурах, к электронам в ме­талле применима классическая статистика, в то же время, когда (Е — Е) < kT, к ним применима только квантовая ста­тистика Ферми — Дирака.

Распределение электронов по различ­ным квантовым состояниям подчиняется принципу Паули, согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) элек­тронов, они должны отличаться какой-то характеристикой, например направлением спина. Следовательно, по квантовой тео­рии, электроны в металле не могут располагаться на самом низшем энергети­ческом уровне даже при О К. Принцип Паули вынуждает электроны взбираться вверх «по энергетической лестнице».

Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми — Дирака . Если μ_o — химический по­тенциал электронного газа при Т = О К, то, среднее число (N(E)) электронов в квантовом состоянии на энергетическом уровне с энергией Е равно

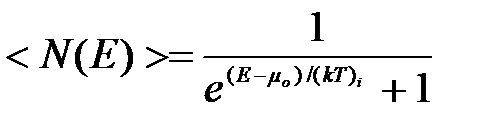(8)

Из (8) следует, что при Т=0 К функция распределения <N(E)> = 1, есл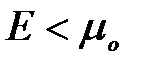и и 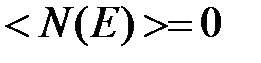, если .

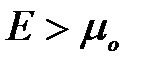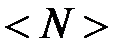
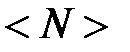
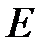
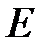
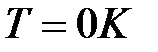
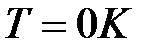
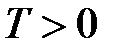
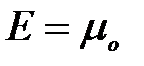
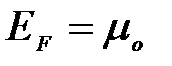
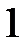
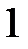
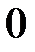
Рис. 1

График этой функции приведен на рис. 1 , а. В области энергий от 0 до 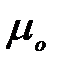функция 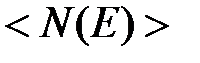равна единице. При 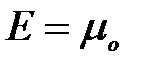она скачкообразно изменяется до нуля.

Это означает, что при Т=0 К все нижние квантовые состояния, вплоть до состояния с энергией 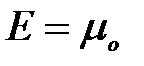, заполнены электронами, а все состояния с энергией, большей 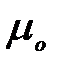, свободны.

Следовательно, есть не что иное, как максимальная энергия, которую могут иметь электроны проводимости в металле при О К.

Эта максимальная энергия называется энергией Ферми и обозначается 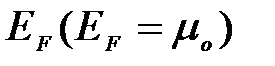.Поэтому рас­пределение Ферми — Дирака обычно за­писывается в виде

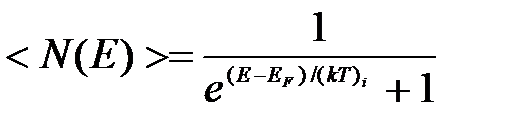(9)

Наивысший энергетический уровень, за­нятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми Е , которую имеют элек­троны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно от­считывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых электронами энерге­тических уровней.