Зонные модели металлов, полупроводников и диэлектриков. Используя уравнение Шредингера — основное уравнение динамики в нереля­тивистской квантовой механике — в принципе можно рассмотреть задачу о кристал­ле

Используя уравнение Шредингера — основное уравнение динамики в нереля­тивистской квантовой механике — в принципе можно рассмотреть задачу о кристал­ле, например найти возможные значения его энергии, а также соответствующие энергетические состояния. Однако как в классической, так и в квантовой меха­нике отсутствуют методы точного решения динамической задачи для системы многих частиц. Поэтому эта задача решается приближенно, путем сведения задачи многих частиц к одноэлектронной задаче — задаче об одном электроне, дви­жущемся в заданном внешнем поле. Подобный путь приводит к зонной тео­рии твердого тела.

В основе зонной теории лежит так называемое адиабатическое приближение. Квантово-механическая система разде­ляется на тяжелые и легкие частицы — ядра и электроны. Поскольку массы и скорости этих частиц значительно разли­чаются, можно считать, что движение электронов происходит в поле непод­вижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Считая, что ядра в узлах кристаллической решетки неподвижны, движение электрона рассматривается в постоянном периодическом поле ядер.

Далее используется приближение само­согласованного поля. Взаимодействие данного электрона со всеми другими электронами заменяется действием на него стационарного электрического поля, обла­дающего периодичностью кристалличе­ской решетки. Это поле создается усред­ненным в пространстве зарядом всех других электронов и всех ядер. Таким образом, в рамках зонной теории много­электронная задача сводится к задаче о движении одного электрона во внешнем периодическом поле — усредненном и со­гласованном поле всех ядер и электро­нов.

Рассмотрим мысленно процесс образо­вания твердого тела из изолированных атомов. Пока атомы изолированы, т. е. находятся друг от друга на макроскопи­ческих расстояниях, они имеют совпадаю­щие схемы энергетических уровней (рис. 1).

Рис. 1

По мере «сжатия» нашей моде­ли до кристаллической решетки, т. е. когда расстояния между атомами станут равны­ми межатомным расстояниям в твердых телах, взаимодействие между атомами приводит к тому, что энергетические уровни атомов смещаются, расщепляются и расширяются в зоны, образуется так называемый зонный энергетический спектр.

Из рис. 1 , на котором показано расщепление уровней как функция рас­стояния r между атомами, видно, что заметно расщепляются и расширяются лишь уровни внешних, валентных электро­нов, наиболее слабо связанных с ядром и имеющих наибольшую энергию, а также более высокие уровни, которые в основ­ном состоянии атома вообще электронами не заняты. Уровни же внутренних элек­тронов либо совсем не расщепляются, либо расщепляются слабо. Таким обра­зом, в твердых телах внутренние электро­ны ведут себя так же, как в изоли­рованных атомах, валентные же электро­ны «коллективизированы» — принадлежат всему твердому телу.

Образование зонного энергетического спектра в кристалле является квантово-механическим эффектом и вытекает из соотношения неопределенностей. В крис­талле валентные электроны атомов, свя­занные слабее с ядрами, чем внутрен­ние электроны, могут переходить от ато­ма к атому через потенциальные барьеры, разделяющие атомы, т. е. перемещаться без изменения полной энергии (туннель­ный эффект). Это приводит к тому, что среднее время жизни т валентного электрона в данном атоме по сравнению с изолированным атомом су­щественно уменьшается и составляет при­мерно 10^-15 с (для изолированного атома оно примерно 10 ^-8 с). Время же жизни электрона в каком-либо состоянии связано с неопределенностью его энергии (шириной уровня) соотношением неопределен­ностей 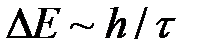. Следователь­но, если естественная ширина спектраль­ных линий составляет примерно 10^-7 эВ, то в кристаллах 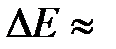1 1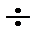0 эВ, т. е. энергетические уровни валентных элек­тронов расширяются в зону дозволенных значений энергии.

Энергия внешних электронов может принимать значения в пределах заштри­хованных на рис. 1 областей, назы­ваемых разрешенными энергетическими зонами. Каждая разрешенная зона «вме­щает» в себя столько близлежащих дискретных уровней, сколько атомов со­держит кристалл: чем больше в кристалле атомов, тем теснее расположены уровни в зоне. Расстояние между соседними энергетическими уровнями в зоне состав­ляет приблизительно 10 ^-22 эВ. Так как оно столь ничтожно, то зоны можно считать практически непрерывными, одна­ко факт конечного числа уровней в зоне играет важную роль в определении ха­рактера распределения электронов по со­стояниям.

Разрешенные энергетические зоны раз­делены зонами запрещенных значений энергии, называемыми запрещенными энергетическими зонами. В запрещенных зонах электроны находиться не могут. Ширина зон (разрешенных и запрещен­ных) не зависит от размера кристалла. Разрешенные зоны 'тем шире, чем слабее связь валентных электронов с ядрами.