А. Разработка многофрагментной модели надежности информационных систем с учетом злонамеренных действий и обновлений программных средств первого рода.
Основные допущения, принимаемые для построения многофрагментных моделей оценивания надежности ПС СВГ с учетом ДВ ЗД, следующие:
- в процессе функционирования СВГ в результате злонамеренных действий изменяется только параметр λKMЗД, а параметры λСЗД и λТЗД остаются постоянными;
- интенсивность проявления ДВ ЗД остается постоянной на промежутках между отказами элемента «Коммутационный модуль», вызванными ДВ ЗД, увеличивается с каждым отказом ПС, и уменьшается с каждым обновлением ПС относительно {λKMЗД}0(0) на величину ΔλKMЗД;
- существует некоторая максимальная интенсивность проявления ДВ ЗД {λKMЗД}max, которая характеризует минимальный временной интервал, требуемый злоумышленникам для нарушения работоспособного состояния элемента СВГ «Коммутационный модуль».
В силу принятых ранее и перечисленных допущений процесс функционирования СВГ может быть представлен как марковский и моделируется с помощью РМФМ.
На рис. 3.43 представлен размеченный граф состояний типовой СВГ (NKM= 3) с учетом ДВ ЗД и обновлений ПС первого рода.
Данный граф можно условно разбить на три зоны фрагментов – исходную Z0, внутреннюю Zj и последнюю ZNz. В свою очередь каждая зона содержит по три вида фрагментов – исходный Ф0, внутренний Фi и последний Фn.
Процесс функционирования СВГ логически определяется следующим образом. В начальный момент система реализует все предписанные функции и находится в состоянии S0(t) зоны фрагментов Z0.
В процессе функционирования элементы системы отказывают и восстанавливаются, вследствие чего система переходит в состояния S1(t) ‑ S9(t) исходного фрагмента Ф0 зоны Z0.
После проявления ДВ ЗД интенсивность отказов элемента «Коммутационный модуль» увеличивается на величину сλ , в результате чего система после восстановления переходит в следующий фрагмент РМФМ зоны Z0, который характеризуется новым параметром {λKMЗД}0(j).
При обновлении ПС система переходит в неработоспособное состояние S10n+18(t), а после обновления ПС переходит в исходный фрагмент новой зоны фрагментов Zj.
Число зон фрагментов можно определить из соотношения:
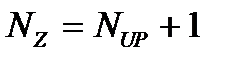 (3.46)
(3.46)
Количество фрагментов модели в зоне фрагментов и значение {λKMЗД}n(j) будут зависеть от параметра начального фрагмента зоны {λKMПС}0(j). и скорости изменения интенсивности сλ. В силу принятых допущений о марковости процессов, протекающих в системе на протяжении существования одного фрагмента МФМ, средняя длительность существования фрагмента определяется из выражения (3.42). Исходя из этого, интенсивность обновления ПС для исходных фрагментов каждой зоны определяется из выражения:
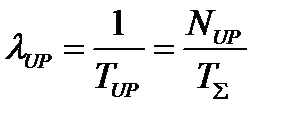 , (3.47)
, (3.47)
где NUP – количество обновлений ПС на протяжении периода эксплуатации системы;
T∑ – период эксплуатации системы (20 лет или 175200 часов [28]).
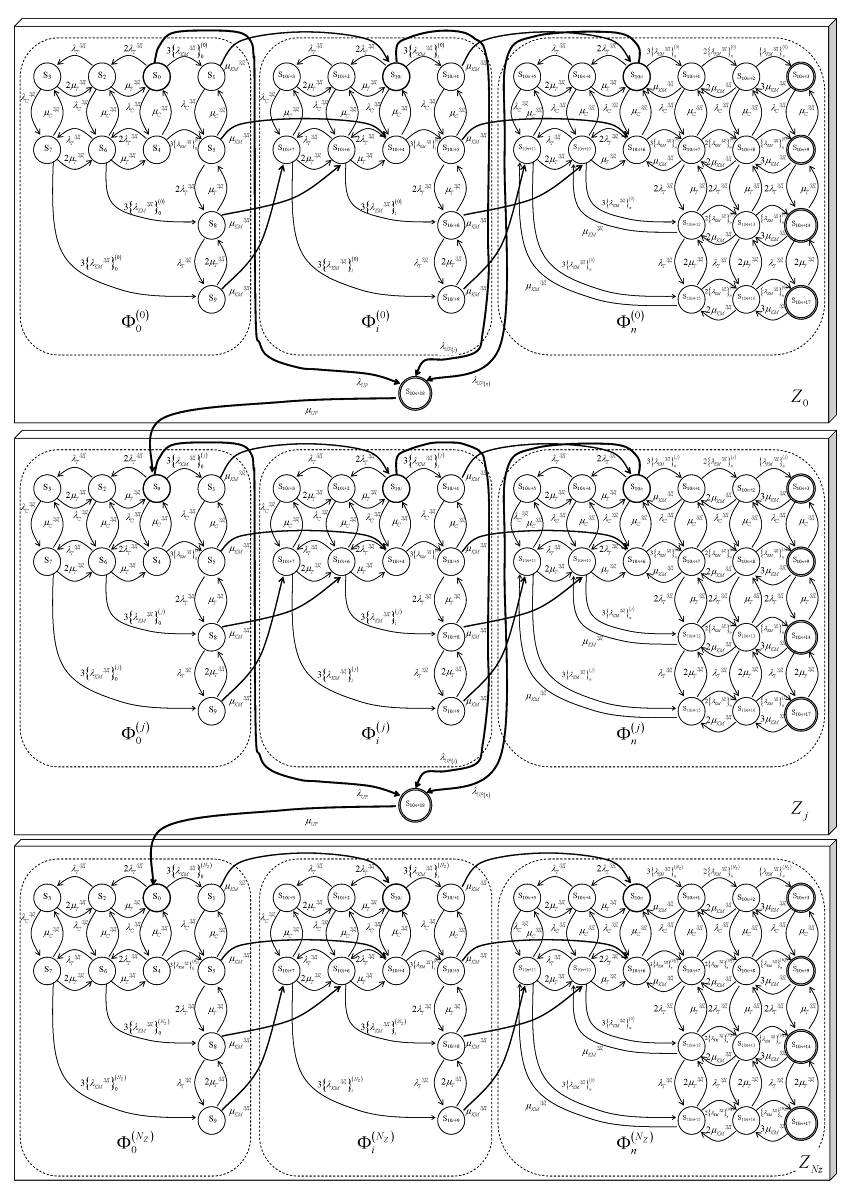
Рис. 3.43 – Размеченный граф состояний и переходов МФМ функционирования СВГ (NKM = 3) с учетом ДВ ЗД и обновлений ПС
первого рода
Для внутренних и последних фрагментов интенсивность обновления ПС определяется следующим образом:
 (3.48)
(3.48)
Для определения количества фрагментов МФМ внутри определенной зоны необходимо руководствоваться одним из условий:
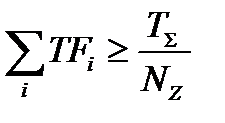 , (3.49)
, (3.49)
или
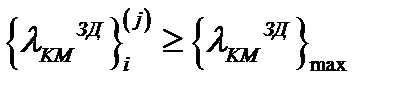 (3.50)
(3.50)
Исходя из анализа модели, определяем, что она имеет регулярный вид. Регулярность заключается в повторении зон фрагментов и фрагментов внутри каждой зоны, что позволяет отследить изменение коэффициента готовности СВГ во времени при изменении ее параметров, используя математический аппарат исследования марковских случайных процессов.
СДУ Колмогорова многофрагментной модели надежности СВГ, построенная по графу состояний и переходов (рис. 3.43), будет состоять из девяти характерных регулярных блоков, описывающих три фрагмента (начальный, внутренние и последний) начальной, внутренней и последней зон модели.
Значение коэффициента технического использования СВГ, граф состояний и переходов которой изображен на рис. 3.43, с учетом ДВ ЗД и обновлений ПС определяется из выражения:
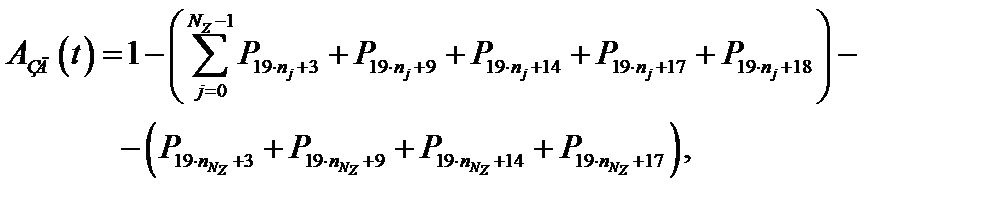 (3.51)
(3.51)
где nj – номер последнего фрагмента j-й зоны фрагментов.
Значения параметров многофрагментной МН СВГ с учетом ДВ ЗД и обновлений ПС первого рода представлены в таблице 3.8, причем значения параметров сλ и {λKMЗД}max одинаковы для всех зон фрагментов.
Таблица 3.8 –Значения параметров многофрагментной
МН СВГ с учетом ДВ ЗД и обновлений
ПС первого рода
| Условное обозначение параметра | Значение параметра |
| {λKMЗД}0(0) | {λKMЗД}0(0)={λKMПС}0(0)=2,52∙10–3 1/час |
| сλ | сλ=1,5 |
| {λKMЗД}max | {λKMЗД}max=0,1 1/час |
| ∆{λKMЗД}(j) | ∆{λKMЗД}(j) = ∆λKMПС = 5∙10–4 1/час |
| {λСЗД}0 | {λСЗД}0=38,58∙10–3 1/час |
| {λТЗД}0 | {λТЗД}0=10,3∙10–3 1/час |
| μKMЗД | μKMЗД=12 1/час |
| μСЗД | μСЗД=4 1/час |
| μТЗД | μТЗД=4 1/час |
| λUP | для NUP = {0,1,2,3} и T∑=175200 часов λUP={∞;1,14∙10–5;1,71∙10–5;2,28∙10–5} (1/час) |
| μUP | μUP=2 1/час |
Для изучения влияния избыточности структуры СВГ на ее надежность рассмотрим СВГ с различным количеством элементов «Коммутационный модуль» (NKM= {1,2,3}). Результаты моделирования представим в виде графической зависимости коэффициента технического использования АЗД(t) СВГ от времени функционирования системы.
На рис. 3.44 - 3.46 на примере СВГ с различным количеством элементов «Коммутационный модуль» показано, как влияет на надежность системы с учетом ДВ ЗД количество обновлений ПС первого рода. При показателях начальной безотказности ПС (λПС 0 = 2,52·10–3 1/час), обеспечивающих более высокий уровень HAL-3, и внешних воздействиях на систему надежность ПС СВГ уменьшается до критического уровня, определяемого параметром λЗД max. Это иллюстрирует кривая (а) на рис.3.44, которая соответствует второму уровню надежности по шкале HAL.
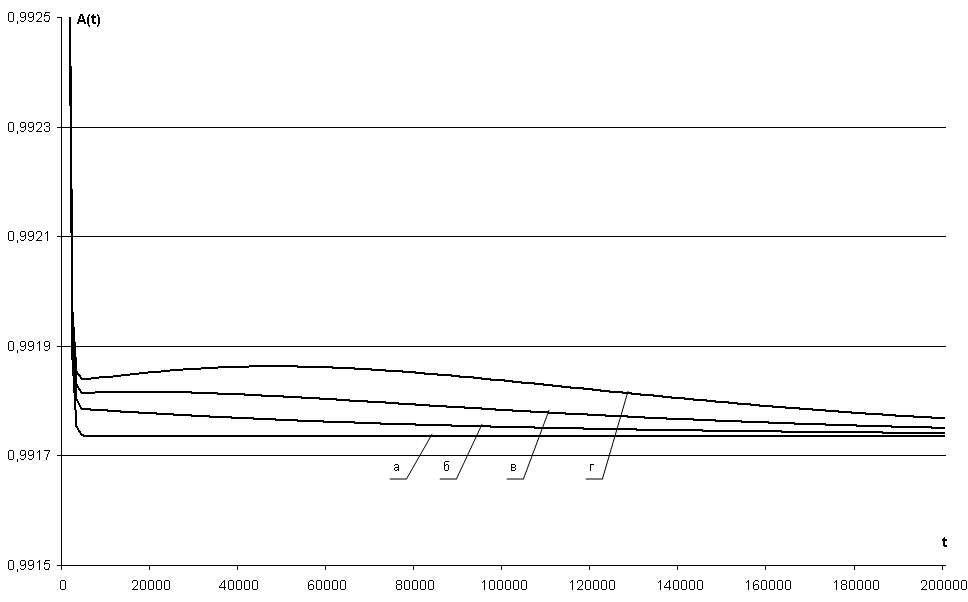
Рис. 3.44 – Зависимость коэффициента технического использования АЗД(t) СВГ (NKM=1) при обновлениях ПС первого рода от времени эксплуатации системы для параметров:
а) NUP = 0; б) λUP=1,14∙10–5 1/час (NUP = 1);
в) λUP=1,71∙10–5 1/час (NUP = 2);
г) λUP=2,28∙10–5 1/час (NUP = 3)
Для заданных параметров модели (таблица 3.8) при обновлениях ПС первого рода, наблюдается рост значений показателя надежности (в среднем на 10–5) в середине интервала эксплуатации системы. При этом в конце интервала эксплуатации наблюдается уменьшение значений показателя АЗД(t) до критического уровня, что иллюстрируют кривые (б), (в) и (г) на рис. 3.44. Рост значений показателя надежности АЗД(t) с увеличением интенсивности обновлений ПС первого рода показывает возможность использования этого явления при обеспечении заданных показателей надежности СВГ с неизбыточной структурой.
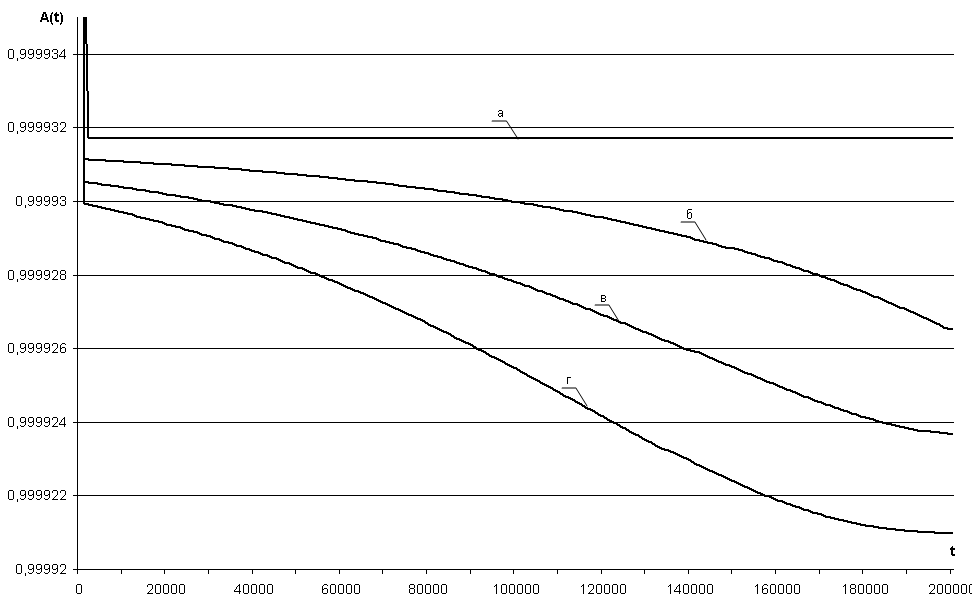
Рис. 3.45 – Зависимость коэффициента технического использования АЗД(t) СВГ (NKM=2) при обновлениях ПС первого рода от времени эксплуатации системы для параметров:
а) NUP = 0; б) λUP=1,14∙10–5 1/час (NUP = 1);
в) λUP=1,71∙10–5 1/час (NUP = 2);
г) λUP=2,28∙10–5 1/час (NUP = 3)
Кривые (а) на рис. 3.45 - 3.46 иллюстрируют повышение надежности ПС СВГ с учетом ДВ ЗД за счет увеличения избыточности структуры системы до уровней HAL-4 и HAL-5 (при условии функциональной автономности избыточных элементов). При отсутствии обновлений ПС значения показателя надежности АЗД(t) также уменьшаются до критического уровня, определяемого параметром λЗД max. Однако при этом избыточность структуры позволяет обеспечить требуемые уровни надежности СВГ (при значении λЗД max = 0,1 1/час). Как показали результаты моделирования, при обновлениях ПС первого рода рост надежности за счет устранения причин отказов ПС незначительный по сравнению с неготовностью, вызванной увеличением длительности простоев системы при обновлениях программ. Поэтому значение показателя АЗД(t) с каждым обновлением ПС уменьшается в среднем на 2·10–6, что иллюстрируют кривые (б), (в) и (г) на рис. 3.45 - 3.46.
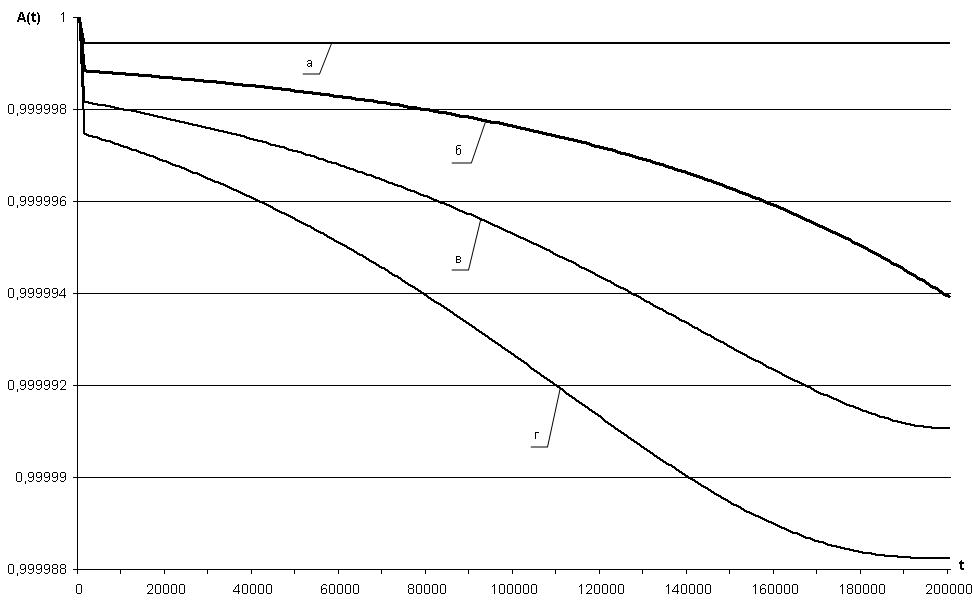
Рис. 3.46 – Зависимость коэффициента технического использования АЗД(t) СВГ (NKM=3) при обновлениях ПС первого рода от времени эксплуатации системы для параметров:
а) NUP = 0; б) λUP=1,14∙10–5 1/час (NUP = 1);
в) λUP=1,71∙10–5 1/час (NUP = 2);
г) λUP=2,28∙10–5 1/час (NUP = 3)
На графиках, изображенных на рис. 3.44 – 3.46, прослеживается однообразный характер изменения коэффициента технического использования СВГ АЗД(t) от времени эксплуатации системы, который имеет следующие характерные особенности:
- характер изменения показателя надежности СВГ зависит от соотношения двух временных интервалов неработоспособности СВГ, определяемых проявлением ДВ ЗД с интенсивностью {λKMЗД}max и проведением обновления ПС первого рода; в случае, когда первый временной интервал больше, увеличение количества обновлений ПС первого рода позволяет повысить готовность системы (как показано на рис. 3.44), в противном случае при увеличении количества обновлений ПС первого рода значение коэффициента технического использования СВГ АЗД(t) уменьшается;
- значения коэффициента технического использования СВГ АЗД(t) ассимптотически стремится к значению стационарного коэффициента АЗД, которое можно определить с помощью марковской МН для параметра λKMЗД = {λKMЗД}max ;
- надежность СВГ с учетом ДВ ЗД и обновлений ПС первого рода возрастает с увеличением количества элементов NKM;
- уменьшение последствий неисправностей СВГ (отказов ее элементов), вызванных ЗД, с помощью обновлений ПС первого рода при заданных параметрах модели позволяет повысить готовность СВГ только для систем с неизбыточной структурой (NKM=1).
Дата добавления: 2015-08-11; просмотров: 2147;
