СВГ с не обновляемым программным обеспечением
Основные допущения, принимаемые для построения многофрагментных моделей оценивания надежности ПС СВГ с учетом ДВ ЗД, следующие:
- в процессе функционирования системы в результате злонамеренных действий изменяется только параметр λKMЗД (это объясняется доступностью элемента системы «Коммутационный модуль» широкому кругу пользователей и подтверждается статистическими данными [28], а параметры λCЗД и λTЗД остаются постоянными;
- интенсивность проявления ДВ ЗД остается постоянной на промежутках между отказами элемента системы «Коммутационный модуль», вызванными ДВ ЗД;
- существует некоторая максимальная интенсивность проявления ДВ ЗД {λKMЗД}max , которая характеризует минимальный временной интервал, требуемый злоумышленникам для нарушения работоспособного состояния элемента системы «Коммутационный модуль» (например, если {λKMЗД}max = 0,1 1/час, то в среднем злоумышленнику необходимо как минимум десять часов для перевода элемента системы «Коммутационный модуль» в неработоспособное состояние). Максимальная интенсивность проявления ДВ ЗД обусловлена рядом характеристик безопасности (security) системы и ее элементов. В ряде случаев значение {λKMЗД}max зависит от того, как быстро будет произведено внеплановое обновление ПС для устранения «дыры» в ПС.
В силу изложенных ранее и перечисленных допущений процесс функционирования СВГ может быть представлен как марковский и моделируется с помощью РМФМ.
Принимая во внимание ряд объективных причин, необходимо рассмотреть МН СВГ с учетом ДВ ЗД для различных значений {λKMЗД}max.
На рис. 3.40 приведена обобщенная РМФМ функционирования типовой системы с учетом ДВ ЗД без учета обновлений ПС при проявлении трех неисправностей данного класса за период эксплуатации системы. Модель представляет собой размеченный марковский граф с регулярной структурой.
Рассмотрим марковский процесс с 8 параметрами и 37 состояниями. Для удобства перехода к более емким моделям, в графе модели начальный фрагмент и его параметры изображены с индексом 0, внутренний фрагмент и его параметры имеют индекс i (для трехфрагментной модели i = 1), а последний фрагмент и его параметры имеют индекс n (для трехфрагментной модели n = 2).
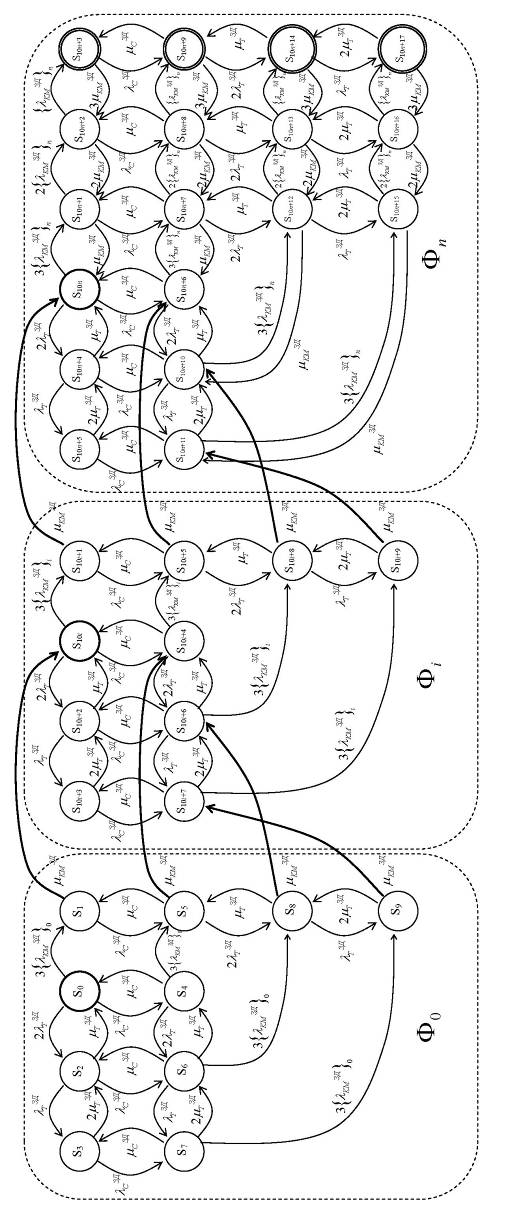
Рис. 3.40 – Размеченный граф состояний и переходов МФМ функционирования СВГ (NKM = 3) с учетом ДВ ЗД
Процесс функционирования СВГ с учетом ДВ ЗД без учета обновлений ПС происходит следующим образом. В начальный момент система реализует все предписанные функции и находится в состоянии S0(t). В процессе функционирования элементы системы отказывают и восстанавливаются, вследствие чего система переходит в состояния S1(t) – S9(t).
После проявления ДВ ЗД интенсивность отказов элемента КМ увеличивается на величину сλ, в результате чего система после восстановления переходит в следующий фрагмент РМФМ, который характеризуется новым параметром {λKMЗД}i.
Количество фрагментов модели и значение {λKMЗД}n будут зависеть от параметра начального фрагмента {λKMПС}0 и скорости изменения интенсивности сλ . В силу принятых допущений о марковости процессов, протекающих в системе на протяжении существования одного фрагмента МФМ, средняя длительность существования фрагмента определяется на основании графа состояний, пример которого приведен на рис. 3.40 и зависит от количества элементов NKM. Значение средней длительности существования фрагмента определяется из выражения:
 . (3.42)
. (3.42)
Для определения количества фрагментов МФМ необходимо руководствоваться одним из условий:
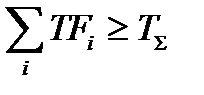 (3.43)
(3.43)
или
 (3.44)
(3.44)
То есть, либо суммарная длительность пребывания системы во всех фрагментах превысит период эксплуатации системы, либо интенсивность отказов ПС СВГ, вызванных ДВ ЗД, достигнет максимального значения.
Анализируя модель определяем, что она имеет регулярный вид. Регулярность заключается в повторении фрагментов, что позволяет отследить изменение коэффициента готовности (технического использования) СВГ во времени при изменении параметров ее защищенности, что проявляется как ДВ ЗД, используя математический аппарат исследования марковских случайных процессов.
СДУ Колмогорова многофрагментной МН СВГ, построенная по графу состояний и переходов, который изображен на рис. 3.40, будет состоять из трех характерных регулярных блоков, описывающих начальный, внутренние и последний фрагменты модели.
Значение коэффициента готовности СВГ, граф состояний и переходов которой изображен на рис. 3.40, с учетом ДВ ЗД определяется из выражения:
 (3.45)
(3.45)
Значения параметров многофрагментной МН СВГ с учетом ДВ ЗД определяются согласно модели параметров, предложенной в предыдущем пункте, и представлены в таблице 3.7, причем значение параметра {λKMЗД}max взято для условий, что злоумышленникам для перевода системы «Коммутационный модуль» в неработоспособное состояние необходимо как минимум 24, 10 либо 2 часа.
Таблица 3.7 – Значения параметров многофрагментной
МН СВГ с учетом ДВ ЗД
| Условное обозначение параметра | Значение параметра |
| {λKMЗД}0 | {λKMЗД}0=2,52∙10–3 1/час |
| {λСЗД}0 | {λСЗД}0=38,58∙10–3 1/час |
| {λТЗД}0 | {λТЗД}0=10,3∙10–3 1/час |
| μKMЗД | μKMЗД=12 1/час |
| μСЗД | μСЗД=4 1/час |
| μТЗД | μТЗД=4 1/час |
| сλ | сλ={0; 1,3; 1,5} |
| {λKMЗД}max | {λKMЗД}max={0,42; 0,1; 0,5} (1/час) |
Для изучения влияния избыточности структуры СВГ на ее надежность рассмотрим СВГ с различным количеством элементов «Коммутационный модуль» (NKM= {1,2,3}). Результаты моделирования представлены в виде графической зависимости коэффициента готовности АЗД(t) СВГ от времени функционирования системы.
На рис. 3.41 на примере СВГ, состоящей из элементов «Сервер», два «Терминала» и один «Коммутационный модуль» показано как влияет на надежность системы значения параметров {λKMЗД}max и сλ .
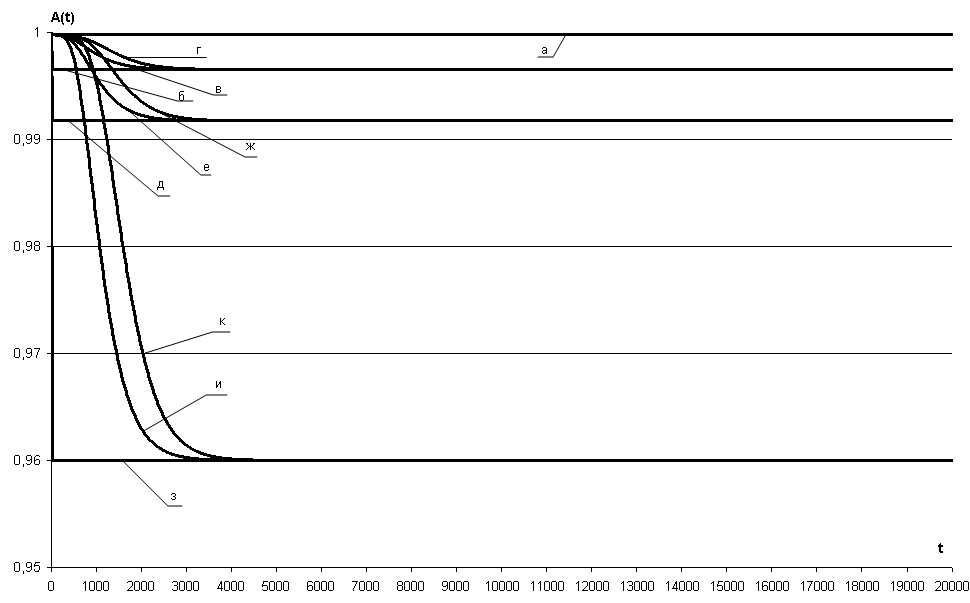
Рис. 3.41 – Зависимость коэффициента готовности АЗД(t) СВГ (NKM=1) от времени эксплуатации системы для параметров:
а) {λKMЗД}0 = 2,52·10–3 1/час, сλ = 0; б) {λKMЗД}0 = 0,042 1/час, сλ = 0;
в) {λKMЗД}0 = 2,52·10–3 1/час, сλ = 1,5, {λKMЗД}max = 0,042 1/час;
г) {λKMЗД}0 = 2,52·10–3 1/час, сλ = 1,3, {λKMЗД}max = 0,042 1/час;
д) {λKMЗД}max = 0,1 1/час, сλ = 0;
е) {λKMЗД}0 = 2,52·10–3 1/час, сλ = 1,5, {λKMЗД}max = 0,1 1/час;
ж) {λKMЗД}0 = 2,52·10–3 1/час, сλ = 1,3, {λKMЗД}max = 0,1 1/час;
з) {λKMЗД}0 = 0,5 1/час, сλ = 0;
и) {λKMЗД}0 = 2,52·10–3 1/час, сλ = 1,5, {λKMЗД}max = 0,5 1/час;
к) {λKMЗД}0 = 2,52·10–3 1/час, сλ = 1,3, {λKMЗД}max = 0,5 1/час
На рис. 3.42 показано, как влияет избыточность (NKM= {1,2,3}) на надежность СВГ с учетом ДВ ЗД. Для наглядности изображения на графике показана зависимость приведенных коэффициентов неготовности от времени эксплуатации СВГ.
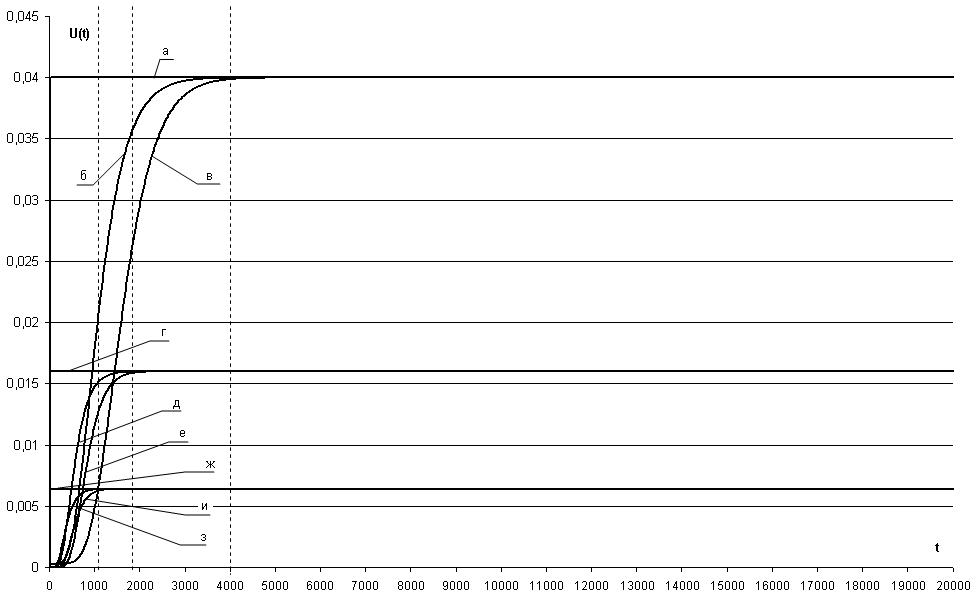
Рис. 3.42 – Зависимость коэффициента неготовности UЗД(t) СВГ от времени эксплуатации системы для параметров:
а) NKM= 1, {λKMЗД}0 = 0,5 1/час, сλ = 0;
б) NKM= 1, {λKMЗД}0 = 2,52·10–3 1/час, {λKMЗД}max = 0,5 1/час, сλ = 1,5;
в) NKM= 1, {λKMЗД}0 = 2,52·10–3 1/час, {λKMЗД}max = 0,5 1/час, сλ = 1,3;
г) NKM= 2, {λKMЗД}0 = 0,5 1/час, сλ = 0;
д) NKM= 2, {λKMЗД}0 = 2,52·10–3 1/час, {λKMЗД}max = 0,5 1/час, сλ = 1,5;
е) NKM= 2, {λKMЗД}0 = 2,52·10–3 1/час, {λKMЗД}max = 0,5 1/час, сλ = 1,3;
ж) NKM= 3, {λKMЗД}0 = 0,5 1/час, сλ = 0;
з) NKM= 3, {λKMЗД}0 = 2,52·10–3 1/час, {λKMЗД}max = 0,5 1/час, сλ = 1,5;
и) NKM= 3, {λKMЗД}0 = 2,52·10–3 1/час, {λKMЗД}max = 0,5 1/час, сλ = 1,3
На рис. 3.42 кривые (г), (д), (е) показывают изменение приведенного коэффициента неготовности для СВГ с NKM=2 UЗД*(t)=10∙UЗД(t), а кривые (ж), (з), (и) показывают изменение приведенного коэффициента неготовности для СВГ с NKM=3 UЗД*(t)=100∙UЗД(t).
На графиках, изображенных на рис. 3.41 - 3.42, прослеживается однообразный характер изменения коэффициента готовности СВГ АЗД(t) (или коэффициента неготовности СВГ UЗД(t)) от времени эксплуатации системы, который имеет следующие характерные особенности:
- количество фрагментов МФМ для параметров МН, приведенных в таблице 3.7, определяется только из условия (3.44);
- значение временного интервала ΔTCT, по истечении которого значение коэффициента готовности (коэффициента неготовности) АЗД(t) (UЗД(t)) будет равно значению стационарного коэффициента готовности (коэффициента неготовности) АЗД (UЗД) (на рис. 3.42 границы этого интервала обозначены пунктирной линией), зависит от параметра сλ.
Анализ результатов исследования рассмотренных моделей позволяет сделать несколько выводов, которые носят общий характер:
- коэффициент готовности СВГ с учетом ДВ ЗД АЗД(t) является функцией, уменьшающейся во времени до значения АЗД, значение которого определяется параметром МН λKMЗД = {λKMЗД}max;
- надежность СВГ с учетом ДВ ЗД возрастает с увеличением количества элементов NKM;
- значение временного интервала ΔTCT, по истечении которого значение коэффициента готовности (коэффициента неготовности) АЗД(t) (UЗД(t)) будет равно значению стационарного коэффициента готовности (коэффициента неготовности) АЗД (UЗД), уменьшается с увеличением количества элементов NKM;
- значение временного интервала ΔTCT уменьшается с увеличением параметра сλ.
Дата добавления: 2015-08-11; просмотров: 1224;
