Многофрагментная модель надежности с учетом обновлений и дефектов программного обеспечения
Рассмотрим модель надежности трехэлементной СВГ с учетом ДП ПС и обновлений ПС первого и второго рода.
На рис. 3.32 - 3.33 приведена обобщенная регулярная МФМ функционирования ПС типовой СВГ при двух обновлениях ПС за период эксплуатации системы. Модель представляет собой размеченный марковский граф с регулярной структурой. Рассматривается марковский процесс с 14-ю параметрами и 55-ю состояниями.
Рис. 3.32 – Упрощенная схема графа состояний и переходов
МФМ функционирования СВГ (NKM = 3) с учетом ДП ПС и обновления ПС
Процесс функционирования ПС СВГ происходит следующим образом. В начальный момент система реализует все предписанные функции и находится в состоянии S0(t). В процессе функционирования элементы системы отказывают и восстанавливаются, вследствие чего система переходит в состояния S1(t) – S17(t). Через определенный временной интервал происходит обновление ПС системы, и она переходит в состояние S18(t), которое при обновлениях ПС первого рода является неработоспособным, а при обновлениях ПС второго рода – работоспособным.
После проведения восстановления изменяются параметры системы {λKMПС}i, {λCПС}i, {λTПС}i и система переходит в новый фрагмент МФМ (состояние S19(t)).
Если предположить, что количество обновлений ПС равно двум, то модель будет состоять из трех фрагментов. Число внутренних фрагментов можно определить из соотношения:
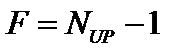 (3.39)
(3.39)
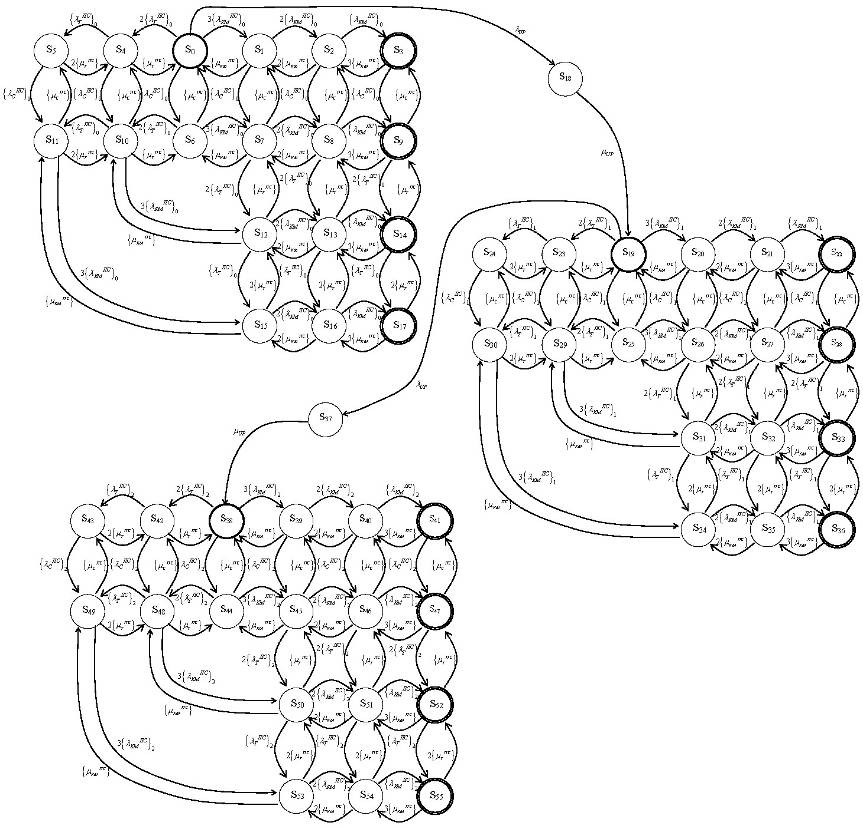
Рис. 3.33 – Размеченный граф состояний и переходов МФМ функционирования типовой СВГ (NKM = 3) с учетом ДП ПС и обновлений ПС
Анализируя модель определяем, что она имеет регулярный вид. Регулярность заключается в повторении фрагментов, что позволяет отследить изменение коэффициента готовности ПС СВГ во времени при изменении параметров ее ПС, используя математический аппарат исследования марковских случайных процессов.
СДУ Колмогорова многофрагментной модели надежности ПС СВГ, построенная по графу состояний и переходов, изображенному на рис. 3.33, будет состоять из трех характерных регулярных блоков, описывающих начальный, внутренние и последний фрагменты модели.
Следует отметить, что в зависимости от значимости временных интервалов обновления ПС СВГ, при обновлениях ПС первого рода результирующим показателем надежности будет либо коэффициент готовности, либо коэффициент технического использования.
Если временной интервал обновления ПС, при котором система находится в состоянии простоя, учитывается при определении общей надежности, то показатель – коэффициент готовности системы, граф состояний и переходов которой изображен на рис. 3.33, определяется из выражения:
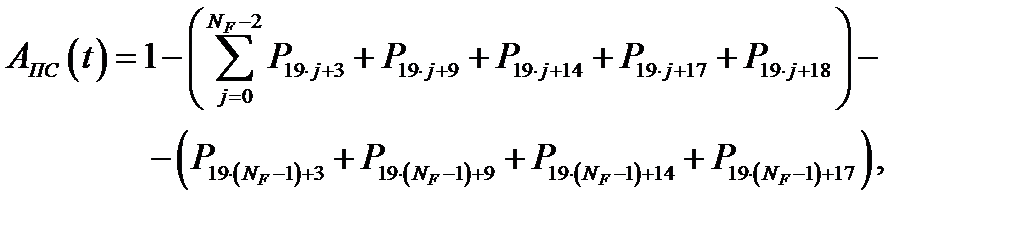 (3.40)
(3.40)
где NF – количество фрагментов модели, NF = NUP +1.
Если временной интервал обновления ПС, при котором СВГ находится в состоянии простоя, не учитывается при определении общей надежности (считается плановым периодом простоя), то значение коэффициента технического использования определяется по (3.40), а значение коэффициента готовности определяется из выражения:
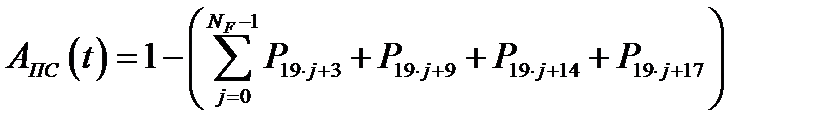 (3.41)
(3.41)
Если для устранения ДП ПС проводятся обновления ПС второго рода, то значения коэффициентов готовности и технического использования СВГ определяются из выражения (3.41).
Приймем следующие значения параметров ПС k=4,2∙10–7, В = 0,95, ER = 2,5, FD = 6 для всех элементов системы.
Значение средней частоты обращений к командам программы зависит от производительности процессора ЭВМ и составляет:
- для элемента «Коммутационный модуль» rКМ = 7,2·109 (строк кода/час);
- для элемента «Сервер» rС = 36·109 (строк кода/час);
- для элемента СВГ «Терминал» rТ = 9,6·109 (строк кода/час).
Интенсивности отказов элементов, вызванных ДП ПС, будут соответственно равны:
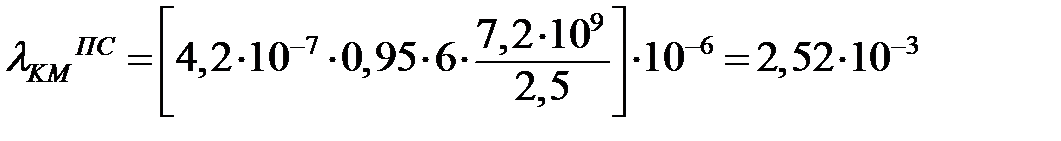 (1/час);
(1/час);
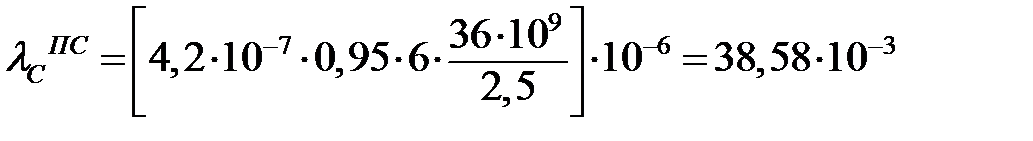 (1/час);
(1/час);
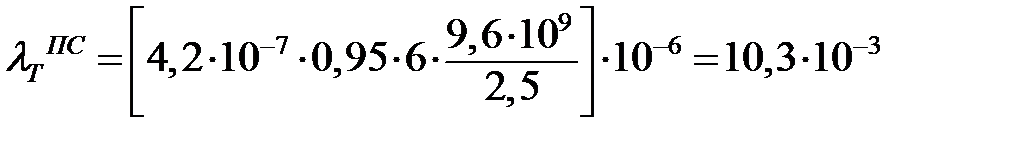 (1/час).
(1/час).
С учетом того, что отказы элементов СВГ, вызванные ДП ПС, устраняются перезапуском программы отказавшего элемента, интенсивности восстановления элементов СВГ после этих отказов будут равны: μKM ПС = 12 1/час; μС ПС = μТ ПС = 4 1/час.
Значение параметра μUP взято усредненным между μUP=1,5 (1/час) для обновлений первого рода (среднее время на установку версии ПС СВГ составляет 40 мин) и μUP=2,5 (1/час) для обновлений второго рода (среднее время на перезапуск ПС СВГ составляет 15 мин).
Для удобства представления значения параметров многофрагментной МН СВГ ЦСК с учетом ДП ПС и обновлений ПС сведены в таблицу 3.6.
Для изучения влияния избыточности структуры СВГ на ее готовность рассмотрим СВГ с различным количеством элементов «Коммутационный модуль» (NKM= {1,2,3}). Результаты моделирования представлены в виде графических зависимостей коэффициентов готовности и технического использования АПС(t) СиТВГ от времени функционирования системы. На рис. 3.34-3.35 показано, как влияет на готовность СВГ с различной степенью избыточности (NKM= {1,2,3}) количество обновлений первого рода.
На рис. 3.36 - 3.38 показано, как влияет на готовность СВГ с различной степенью избыточности (NKM= {1,2,3}) количество обновлений второго рода.
Таблица 3.6 – Значения параметров РМФМ СВГ с
учетом ДП ПС и обновлений ПС
| Условное обозначение параметра | Значение параметра |
| {λKMПС}0 | {λKMПС}0=2,52∙10–3 1/час |
| {λСПС}0 | {λСПС}0=38,58∙10–3 1/час |
| {λТПС}0 | {λТПС}0=10,3∙10–3 1/час |
| μKMПС | μKMПС=12 1/час |
| μСПС | μСПС=4 1/час |
| μТПС | μТПС=4 1/час |
| {∆λKMПС}i, {∆λCПС}i, {∆λTПС}i | ∆λKMПС=∆λCПС=∆λTПС=5∙10–4 1/час (для обновлений ПС первого рода) ∆λKMПС=∆λCПС=∆λTПС=10–5 1/час (для обновлений ПС второго рода) |
| μUP | μUP=2 1/час |
| λUP | для NUP = {0,1,2,3} и T∑=175200 часов λUP={∞;1,14∙10–5;1,71∙10–5;2,28∙10–5} (1/час) |
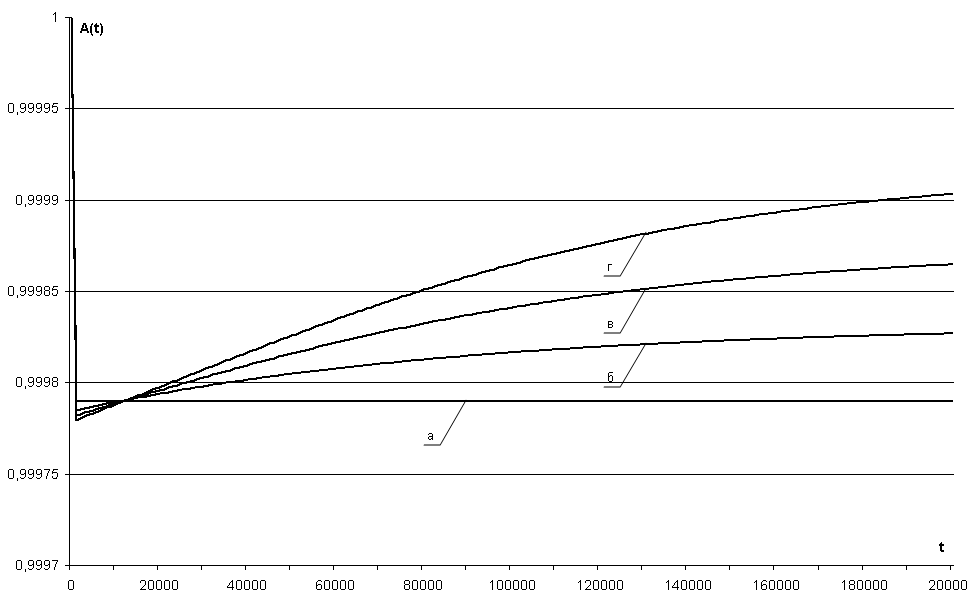
Рис. 3.34 – Зависимость коэффициента технического использования АПС(t) СВГ (NKM = 1) при обновлениях ПС первого рода от времени эксплуатации системы для параметров: а) NUP = 0; б) NUP = 1; в) NUP = 2; г) NUP = 3
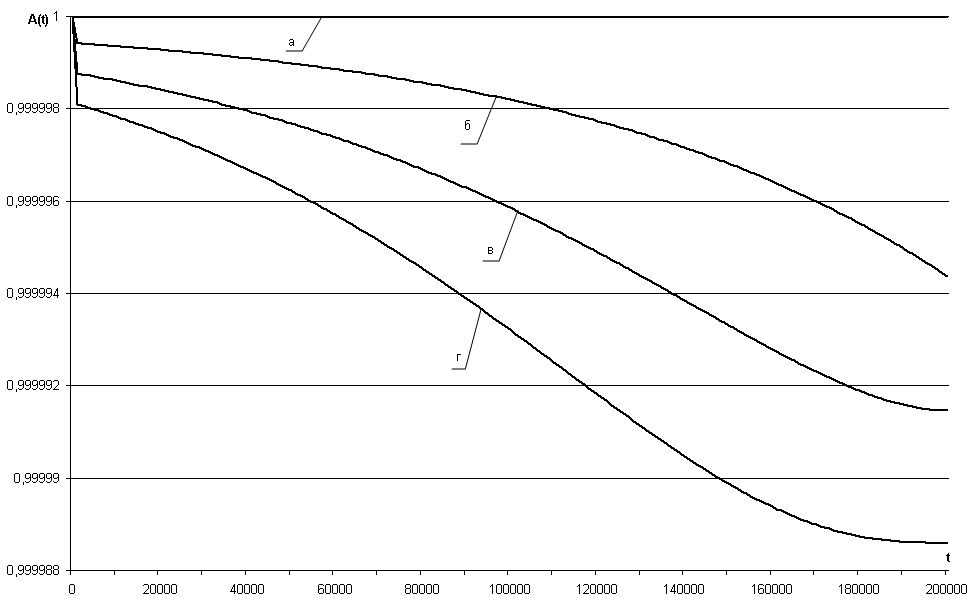
Рис. 3.35 – Зависимость коэффициента технического использования АПС(t) СВГ (NKM = {2, 3}) при обновлениях ПС первого рода от времени эксплуатации системы для параметров:
а) NUP = 0; б) NUP = 1; в) NUP = 2; г) NUP = 3
Надежность СВГ, в состав которой входит один «Коммутационный модуль», при указанных в таблице 3.6 значениях интенсивностей отказов и восстановлений ПС соответствует уровню HAL-3 (0,999). Это иллюстрирует кривая (а) на рис. 3.34. При условии устранения старых и невнесения новых дефектов ПС в процессе их обновлений, готовность ПС системы на этапе эксплуатации будет увеличиваться, что иллюстрируют кривые (б), (в) и (г) на рис. 3.34. При постоянном значении изменения интенсивности отказов ПС ∆λПС= 5·10–4 1/час наблюдается прирост коэффициента технического использования ∆АПС=2·10–5 с каждой новой процедурой обновления ПС. Однако следует учесть, что максимальное значение показателя надежности находится в конце этапа эксплуатации системы, что показывает низкую эффективность обновлений ПС первого рода, как средства повышения надежности системы. Кроме того, существует вероятность внесения новых дефектов при выполнении процедур обновлений ПС, а также величина изменения интенсивности отказов ПС ∆λПС может уменьшаться при каждом обновлении ПС. Поэтому график на рис. 3.34 иллюстрирует повышение точности оценивания показателя АПС(t) с учетом изменения интенсивности отказов ПС, вызванных ДП.
Применение избыточной структуры построения СВГ с функциональной автономностью элементов «Коммутационного модуля» при принятых допущениях и значениях интенсивностей отказов ПС, вызванных ДП, и восстановлений ПС из таблицы 3.6 позволяют обеспечить пятый уровень готовности ПС СВГ по шкале HAL (0,99999). Это иллюстрирует кривая (а) на рис. 3.35. Выполнение процедур обновлений ПС первого рода требует перерыва в функционировании всех элементов СВГ, вследствие чего увеличивается суммарная длительность простоев системы. При значениях изменения интенсивности отказов ПС ∆λПС= 5·10–4 1/час увеличение готовности ПС системы с избыточной структурой при обновлениях ПС незначительно по сравнению с неготовностью, которую вносит увеличение длительности простоев ПС системы. В результате этого с каждым новым обновлением ПС первого рода надежность системы уменьшается на величину ∆АПС= 2,5·10–6.
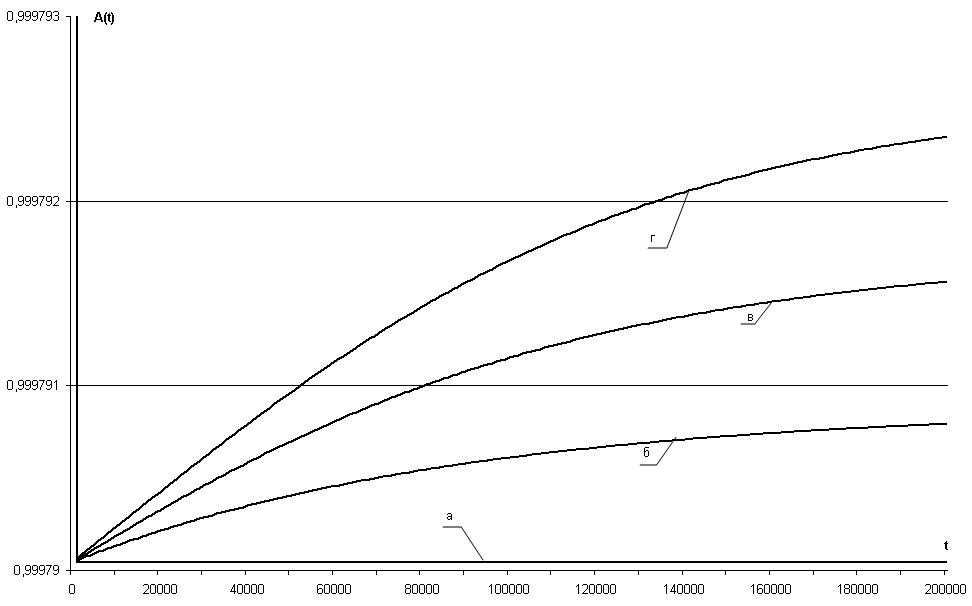
Рис. 3.37 – Зависимость коэффициента готовности АПС(t) СВГ (NKM = 1) при обновлениях ПС второго рода от времени эксплуатации системы для: а) NUP = 0; б)NUP = 1; в)NUP = 2; г) NUP = 3
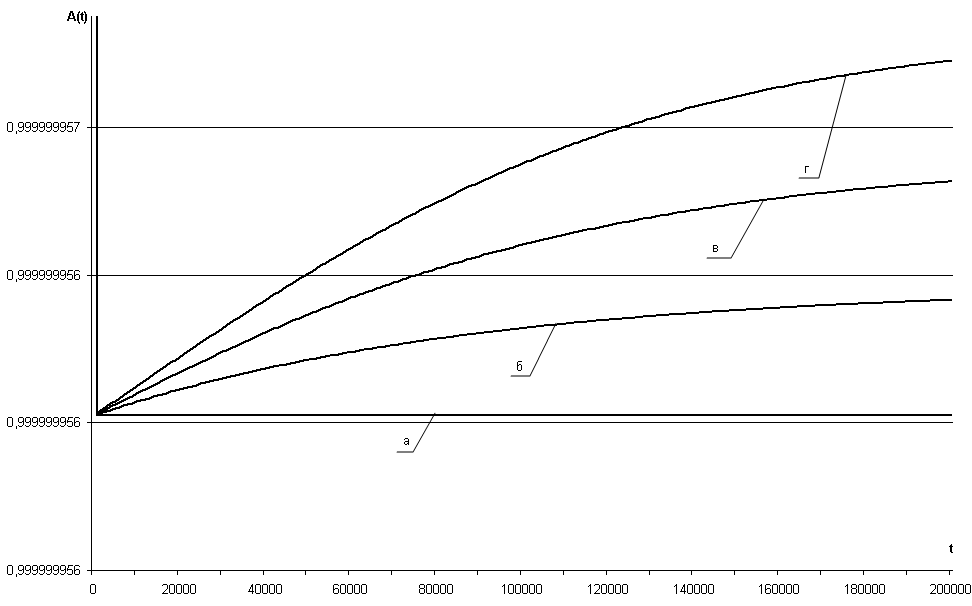
Рис. 3.38 – Зависимость коэффициента готовности АПС(t)
СВГ (NKM = 2) при обновлениях ПС второго рода от времени эксплуатации системы для параметров: а) NUP = 0; б) NUP = 1; в) NUP = 2; г) NUP = 3
В случае проведения обновлений ПС второго рода для ПС СВГ с неизбыточной структурой (NKM = 1) наблюдается незначительное увеличение показателя надежности АПС(t) (в среднем на 1,5·10–6) с каждым обновлением. При этом значение изменения интенсивности отказов ПС является постоянной величиной, равной ∆λПС= 10–5 1/час.
В связи с неравномерностью увеличения показателя АПС(t) на протяжении эксплуатации системы, применение обновлений ПС второго рода для повышения надежности ПС в аспекте проявления ДП неэффективно. Это подтверждается опытными данными, полученными при эксплуатации СВГ [27], которые показывают, что как правило, обновления ПС второго рода проводятся для устранения небольшого количества (1-3) обнаруженных критических дефектов ПС, которые используются злоумышленниками для проведения атак на готовность системы.
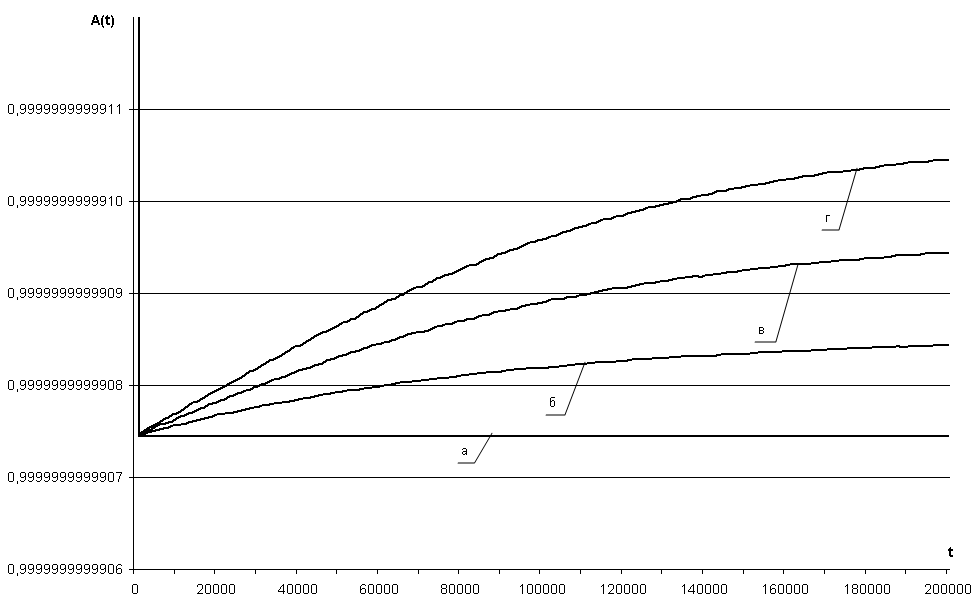
Рис. 3.39 – Зависимость коэффициента готовности АПС(t) СВГ (NKM = 3) при обновлениях ПС второго рода от времени эксплуатации системы для параметров: а) NUP = 0; б) NUP = 1; в) NUP = 2; г) NUP = 3
В случае использования избыточных структур СВГ, увеличение надежности ПС при постоянном изменении интенсивности отказов ПС ∆λПС= 10–5 1/час составляет 10–8-10–12. Из этого следует вывод о том, что повышение надежности ПС СВГ целесообразно проводить за счет повышения избыточности логической структуры системы. Это можно обеспечить за счет увеличения диверсности ПС системы, либо за счет повышения функциональной автономности ПС избыточных элементов СВГ типа «Коммутационный модуль».
Применение МФМ и учет изменения интенсивности отказов ПС, вызванных ДП, при обновлениях программ позволяет повысить точность оценивания показателя АПС(t). При принятых значениях параметров модели (таблица 3.6) абсолютная погрешность определения коэффициента готовности АПС(t) согласно рисункам 3.38 - 3.39 составляет ∆АПС = 10–7.
Анализ результатов исследования рассмотренных моделей позволяет сделать несколько выводов, которые носят общий характер:
- надежность СВГ увеличивается с увеличением количества избыточных элементов (элементов СВГ «Коммутационный модуль»);
- характер изменения надежности СВГ зависит от соотношения двух временных интервалов неработоспособности систем, определяемых проявлением ДП ПС и проведением обновления ПС первого рода. В случае, когда первый временной интервал больше, увеличение количества обновлений ПС первого рода позволяет повысить надежность системы (как показано на рис. 3.34), если же первый временной интервал меньше - при увеличении количества обновлений ПС первого рода надежность системы уменьшается;
- с увеличением количества обновлений ПС второго рода надежность СВГ увеличивается (это объясняется устранением ДП ПС после обновления ПС);
- с увеличением количества избыточных элементов, возрастание коэффициента готовности (технического использования), вызванное увеличением количества обновлений второго рода, уменьшается;
- учет изменения интенсивности проявления ДП ПС позволяет повысить точность оценивания показателя готовности СВГ в зависимости от количества избыточных элементов и значений параметров {∆λKMПС}i, {∆λCПС}i, {∆λTПС}i на 1-3%.
Дата добавления: 2015-08-11; просмотров: 1310;
