Б. Разработка многофрагментной модели надежности информационных систем с учетом злонамеренных действий и обновлений программных средств второго рода.
В отличие от рассмотренных ранее моделей надежности, в которых описывались периодические обновления ПС первого рода (и поэтому модель можно было описать небольшим количеством фрагментов МФМ), количество фрагментов в моделе надежности СВГ с учетом обновлений второго рода может быть очень большим. Обновления ПС второго рода (patches) производятся не периодично, а через некоторое время после проявления ДВ ЗД. Учитывая эти обстоятельства, граф состояний и переходов, описывающий функционирование СВГ с учетом ДВ ЗД и обновлений ПС второго рода, будет выглядеть так, как показано на рис. 3.47 (в качестве примера взята типовая СВГ с NKM = 3).
Процесс функционирования СВГ логически определяется следующим образом. В начальный момент система реализует все предписанные функции и находится в состоянии S0(t) зоны фрагментов Z0. В процессе функционирования элементы системы отказывают и восстанавливаются, вследствие чего система переходит в состояния S1(t) – S9(t) исходного фрагмента Ф0 зоны Z0.
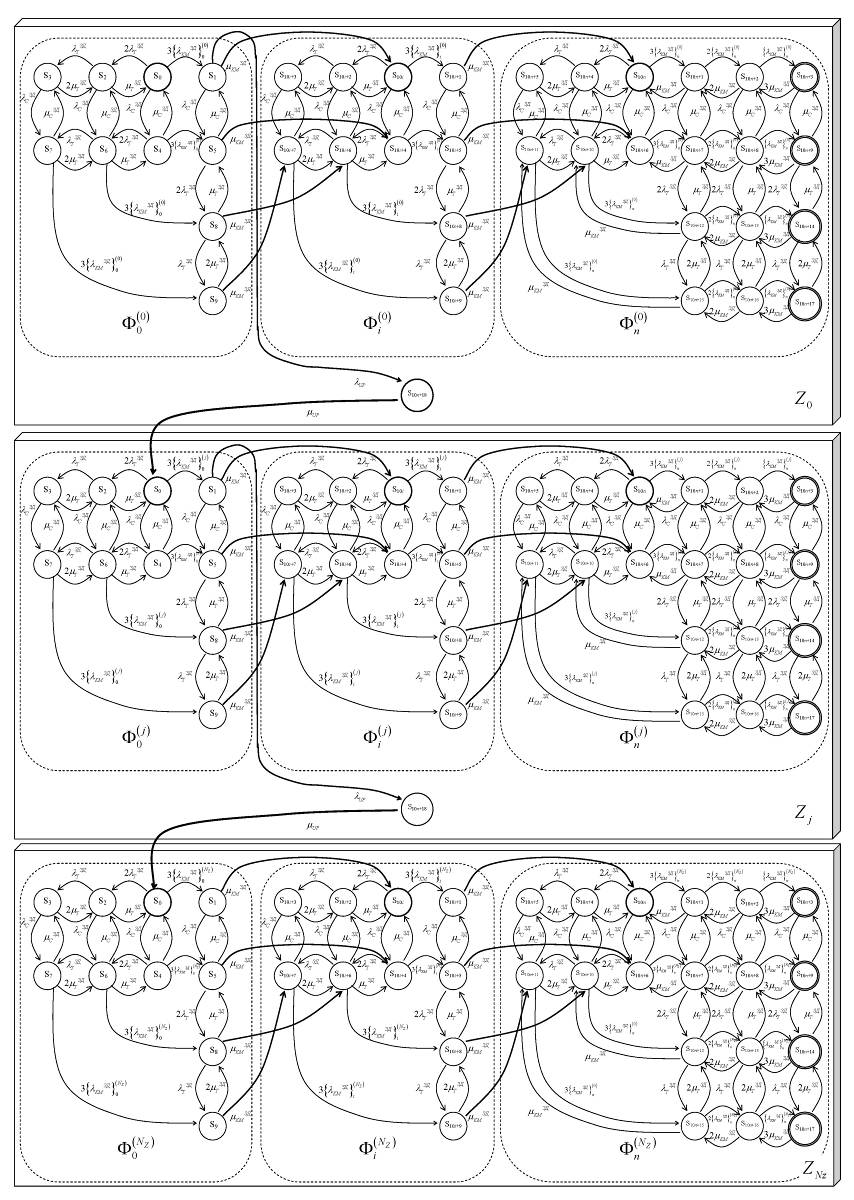
Рис. 3.47 – Размеченный граф состояний и переходов МФМ функционирования СВГ (NKM = 3) с учетом ДВ ЗД и обновлений ПС
второго рода
После проявления ДВ ЗД интенсивность отказов элемента «Коммутационный модуль» увеличивается на величину сλ , в результате чего система после восстановления переходит в следующий фрагмент РМФМ зоны Z0, который характеризуется новым параметром {λKMЗД}0(j).
После первого проявления ДВ ЗД (перехода системы в состояние S1(t) ), разработчики ПС СВГ уведомляются об обнаруженном изъяне («дыре» ПС). Через некоторый временной интервал разработчики ПС создают «заплату», с помощью которой производится обновление ПС СВГ второго рода и система переходит в состояние S10n+18(t) (работоспособное состояние).
После обновления ПС система переходит в исходный фрагмент новой зоны фрагментов Zj.
В связи с большим количеством неопределенности условий создания «заплат» ПС, интенсивность обновлений ПС второго рода может быть определена по закону:
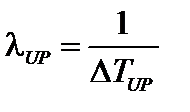 , (3.52)
, (3.52)
где ∆TUP - временной интервал создания «заплаты» ПС СВГ.
Количество фрагментов модели в зоне фрагментов и значение {λKMЗД}n(j). будут зависеть от параметра начального фрагмента зоны {λKMПС}0(j)., скорости изменения интенсивности сλ и интенсивности обновлений ПС второго рода. В силу принятых допущений о марковости процессов, протекающих в системе на протяжении существования одного фрагмента МФМ, средняя длительность существования фрагмента определяется из выражения (3.42).
Исходя из этого, количество фрагментов NF(j) внутри j-й зоны фрагментов определяется итеративно при условии обеспечения равенства:
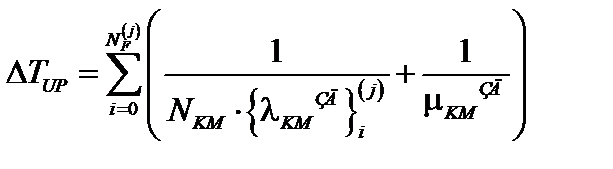 (3.53)
(3.53)
Число зон фрагментов зависит от количества изъянов («дыр») в ПС и может быть большим, что делает МН СВГ с учетом ДВ ЗД и обновлений ПС второго рода громоздкой и сложной для вычислений. В связи с этим целесообразно исследовать данную модель в периодическом аспекте.
Исходя из анализа модели, следует вывод о том, что она имеет регулярный вид. Регулярность заключается в повторении зон фрагментов и фрагментов внутри каждой зоны, что позволяет отследить изменение коэффициента готовности СВГ во времени, при изменении ее параметров используя математический аппарат исследования марковских случайных процессов.
СДУ Колмогорова многофрагментной МН СВГ, построенная по графу состояний и переходов (рис. 3.47), будет состоять из девяти характерных регулярных блоков, описывающих три фрагмента (начальный, внутренние и последний) начальной, внутренней и последней зон модели.
Значение коэффициента готовности СВГ, граф состояний и переходов которой изображен на рис. 3.47, с учетом ДВ ЗД и обновлений ПС второго рода определяется из выражения:
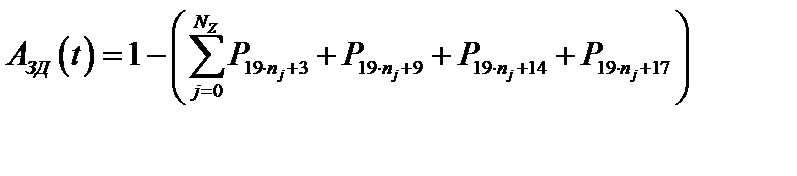 (3.54)
(3.54)
где nj – номер последнего фрагмента j-й зоны фрагментов.
Значения параметров многофрагментной МН СВГ с учетом ДВ ЗД и обновлений ПС второго рода представлены в таблице 3.8, причем значение параметров сλ одинаково для всех зон фрагментов, значение {λKMЗД}i(j) в любом случае не превышает {λKMЗД}max = 0,5 (1/час).
В связи с тем, что при обновлениях ПС второго рода производится небольшое изменение программного кода, значение ∆{λKMЗД}(j) невелико, ∆{λKMЗД}(j) = 1,14∙10–5 и поэтому количество фрагментов внутри зон будет одинаковым.
Равенство (3.51) для значений параметров, указанных в таблице 3.9, выполняется при следующих значениях NF(j) (для СВГ с NKM = 3):
- при ∆TUP= 100 часов, NF(j)=1, {λKMЗД}NF(j) =0,011 (1/час);
- при ∆TUP= 300 часов, NF(j)=4, {λKMЗД}NF(j) =0,026 (1/час);
- при ∆TUP= 500 часов, NF(j)=12, {λKMЗД}NF(j) =0,5 (1/час).
Таблица 3.9 – Значения параметров многофрагментной
МН СВГ с учетом ДВ ЗД и обновлений
ПС второго рода
| Условное обозначение параметра | Значение параметра |
| {λKMЗД}0(0) | {λKMЗД}0(0)={λKMПС}0(0)=2,52∙10–3 1/час |
| сλ | сλ=1,5 |
| ∆{λKMЗД}(j) | ∆{λKMЗД}(j) = ∆λKMПС = 1∙10–5 1/час |
| {λСЗД}0 | {λСЗД}0=38,58∙10–3 1/час |
| {λТЗД}0 | {λТЗД}0=10,3∙10–3 1/час |
| μKMЗД | μKMЗД=12 1/час |
| μСЗД | μСЗД=4 1/час |
| μТЗД | μТЗД=4 1/час |
| λUP | для ∆TUP= {100;300;500} часов λUP={1∙10–2; 3,3∙10–3; 2∙10–3} (1/час) |
| μUP | μUP=2 1/час |
Для изучения влияния количества зон фрагментов МФМ на результаты моделирования были рассмотрены МФМ СВГ (NKM = 3) с различным количеством зон фрагментов модели (NZ = {1,2,3}).
Результаты моделирования представлены в виде графической зависимости коэффициента готовности АЗД(t) СВГ от времени функционирования системы.
На графиках (рис. 3.48 – 3.50) на примере СВГ с количеством элементов «Коммутационный модуль» NKM = 3 показано как влияет на готовность системы с учетом ДВ ЗД интенсивность обновлений ПС второго рода.
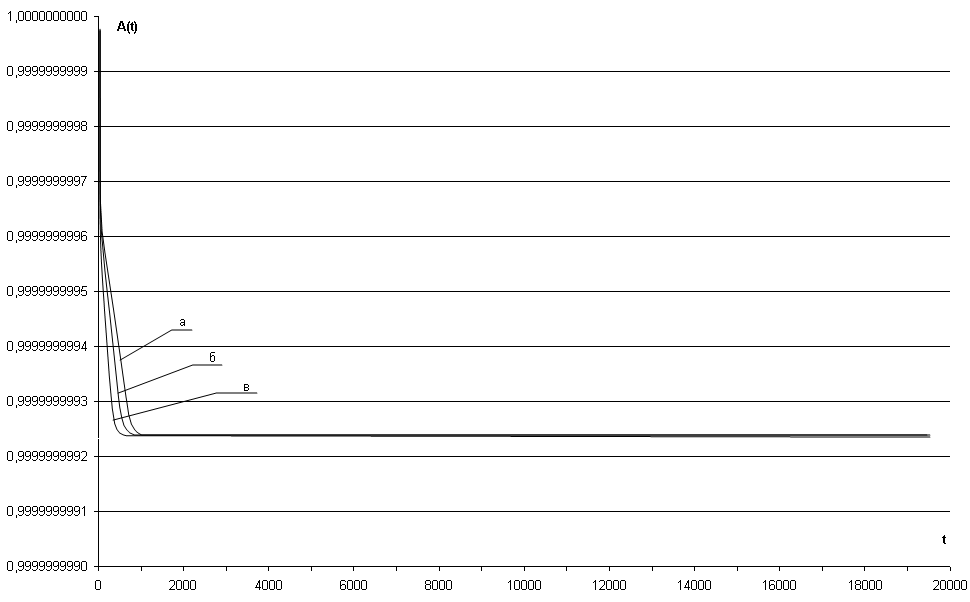
Рис. 3.48 – Зависимость коэффициента готовности АЗД(t) СВГ (NKM=3) при обновлениях ПС второго рода от времени эксплуатации системы для параметров: а) ΔTUP = 100 часов, NZ = 3; б) ΔTUP = 100 часов, NZ = 2; в) ΔTUP = 100 часов, NZ = 1
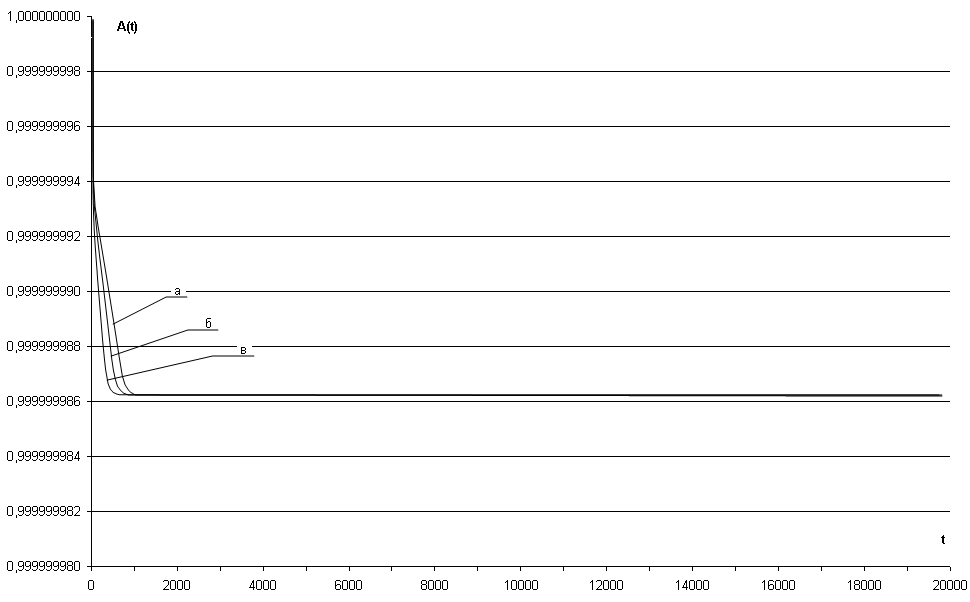
Рис. 3.49 – Зависимость коэффициента готовности АЗД(t) СВГ (NKM=3) при обновлениях ПС второго рода от времени эксплуатации системы для параметров: а) ΔTUP = 300 часов, NZ = 3; б) ΔTUP = 300 часов, NZ = 2; в) ΔTUP = 300 часов, NZ = 1
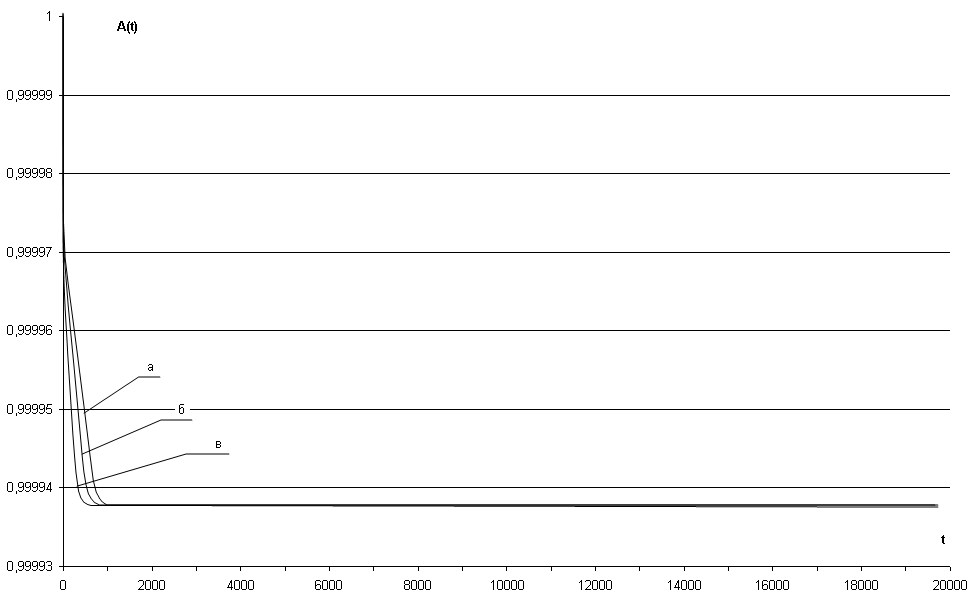
Рис. 3.50 – Зависимость коэффициента готовности АЗД(t) СВГ (NKM=3) при обновлениях ПС второго рода от времени эксплуатации системы для параметров: а) ΔTUP = 500 часов, NZ = 3; б) ΔTUP = 500 часов, NZ = 2; в) ΔTUP = 500 часов, NZ = 1
На указанных графиках прослеживается однообразный характер изменения коэффициента готовности АЗД(t) от времени эксплуатации системы, который имеет следующие характерные особенности:
- значение коэффициента готовности СВГ АЗД(t) уменьшается при увеличении временного интервала создания «заплат» ПС СВГ (при уменьшении интенсивности обновлений ПС второго рода);
- при увеличении количества зон фрагментов значение коэффициента готовности СВГ АЗД(t) быстрее достигает стационарного значения АЗД;
- значение стационарного коэффициента готовности АЗД, можно определить с помощью марковской МН для параметра λKMЗД={λKMЗД}NF(j);
- коэффициент готовности СВГ с учетом ДВ ЗД АЗД(t) и обновлений ПС второго рода является функцией, уменьшающейся во времени до значения АЗД, значение которого определяется параметром МН λKMЗД={λKMЗД}NF(j);
- уменьшение последствий неисправностей СВГ (отказов ее элементов «Коммутационный модуль»), вызванных злонамеренными действиями с помощью обновлений ПС второго рода позволяет повысить надежность СВГ в случае, если «заплаты» ПС разработаны своевременно;
- с увеличением количества элементов NKM надежность СВГ с учетом ДВ ЗД и обновлений ПС второго рода возрастает, однако, при этом для своевременного устранения ДВ ЗД необходимо, чтобы «заплаты» ПС были разработаны за меньший временной интервал ΔTUP.
Дата добавления: 2015-08-11; просмотров: 1557;
