Квантовые статистики Бозе-Эйнштейна и Ферми –Дирака

В отличие от исходных положений классической статистической физики, в ко­торой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основывает­ся на принципе неразличимости тождест­венных частиц. При этом оказывается, как будет показано ниже, что коллективы частиц с целым и полуцелым спинами подчиняются разным статис­тикам.

Пусть система состоит из N частиц. Введем в рассмотрение многомерное про­странство всех координат и импульсов частиц системы. Каждой точке такого пространства соответствует 6N чисел, так как состояние каждой частицы определяет­ся тройкой координат х, у, z и тройкой соответствующих проекций импульса p_x, p_y, p_z. Соответственно число «взаимно перпендикулярных» координатных осей данного пространства равно 6N. Подоб­ное 6N-мерное пространство называется фазовым пространством. Каждому микро­состоянию системы отвечает точка в 6N-мерном фазовом пространстве, так как задание точки фазового пространства означает задание координат и импульсов всех частиц системы. Разобьем фазовое пространство на малые 6N-мерные эле­ментарные ячейки объемом dq dp = dq₁ dq₂ . . . dq_3Ndp_ldp_2. . . dp_3N, где q - со­вокупность координат всех частиц, р — со­вокупность проекций их импульсов. Кор­пускулярно-волновой дуализм свойств частиц вещества и соотноше­ние неопределенностей Гейзенберга приводят к выводу, что объем эле­ментарной ячейки (он называется фазовым объемом) не может быть меньше чем h³ (h — постоянная Планка). Вероятность dW данного состояния системы можно представить с помощью функции распределения f(q, р):

dW = f (q,p) dq dp. (1)

Здесь dW —вероятность того, что точка фазового пространства попадет в элемент фазового объема dq dp, расположенного вблизи данной точки q, р. Иными сло­вами, dW представляет собой вероят­ность того, что система находится в состоянии, в котором ее координаты и импульсы заключены в интервале q, q + dq и р, р + dp.

Согласно формуле ( 1 ), функция рас­пределения есть не что иное, как плот­ность вероятности определенного состоя­ния системы. Поэтому она должна быть, нормирована на единицу:

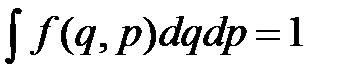
где интегрирование производится по всему фазовому пространству.

Зная функцию распределения f (q, р), можно решить основную задачу кванто­вой статистики — определить средние зна­чения величин, характеризующих рас­сматриваемую систему. Среднее значение любой функции

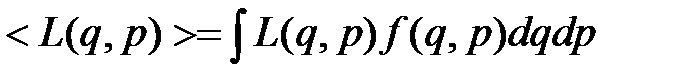(2)

Если иметь дело не с координатами и импульсами, а с энергией, которая квантуется, то состояние системы характе­ризуется не непрерывной, а дискретной функцией распределения.

Явное выражение функции распределе­ния в самом общем виде получил амери­канский физик Д. Гиббс (1839— 1903). Оно называется каноническим распределением Гиббса. В квантовой статистике канони­ческое распределение Гиббса имеет вид

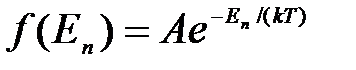(3)

где А — постоянная, определяемая из усло­вия нормировки к единице, и — совокуп­ность всех квантовых чисел, характери­зующих данное состояние. Подчеркнем, что 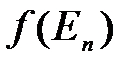есть именно вероятность данного состояния, а не вероятность того, что система имеет определенное значение энергии 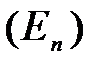, так как данной энергии может соответствовать не одно, а несколь­ко различных состояний (может иметь место вырождение).

Одним из важнейших объектов изуче­ния квантовой статистики, как и класси­ческой, является идеальный газ. Это свя­зано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невзаимодействую­щих частиц задается с помощью так называемых чисел заполнения n —чисел, указывающих степень заполнения кванто­вого состояния, характеризуемого данным набором i квантовых чисел, частицами системы, состоящей из многих тождест­венных частиц. Для систем частиц, обра­зованных бозонами — частицами с нуле­вым или целым спином , числа заполнения могут принимать любые целые значения: 0, 1, 2,... . Для систем частиц, образованных фермионами — частицами с полуцелым спином , числа заполнения могут при­нимать лишь два значения: О—для сво­бодных состояний и 1 — для занятых. Сумма всех чисел заполне­ния должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения <N_i,>.

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бо­зе — Эйнштейна. Распределение бозонов по энергиям вытекает из так называемо­го большого канонического распределе­ния Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым:

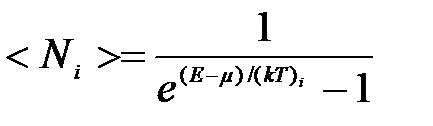(4)

Это распределение называется распреде­лением Бозе — Эйнштейна. Здесь <N_i> — среднее число бозонов в квантовом состоя­нии с энергией E_i, k — постоянная Больцмана, Т — термодинамическая температу­ра, μ — химический потенциал. Он опре­деляет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутрен­няя энергия, фиксированы.

Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми - Дирака . Распределение фер­мионов по энергиям имеет вид

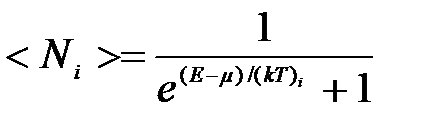(5)

где <N,> — среднее число фермионов в квантовом состоянии с энергией E_i, μ — химический потенциал. Это распределение называется распределением Ферми — Ди­рака.

Если 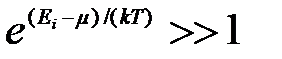, то распределения Бозе — Эйнштейна и Ферми — Ди­рака переходят в классическое распределение Максвелла — Больцмана:

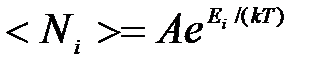(6)

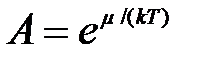где (7)

Таким образом, при высоких температу­рах оба «квантовых» газа ведут себя подобно классическому газу.

Система частиц называется вырожден­ной, если ее свойства существенным об­разом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырож­дение газов становится существенным при весьма низких температурах и больших плотностях. Параметром вырождения на­зывается величина А. При 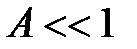, т.е. при малой степени вырождения, распре­деления Бозе — Эйнштейна и Ферми — Дирака ( 4 ) переходят в класси­ческое распределение Максвелла — Больцмана .

Температурой вырождения Т_о назы­вается температура, ниже которой отчет­ливо проявляются квантовые свойства идеального газа, обусловленные тождест­венностью частиц, т.е. Т_о— температура, при которой вырождение становится су­щественным. Если Т » Т_о, то поведение системы частиц (газа) описывается клас­сически.