Движение свободной частицы

При движении свободной частицы (U(х)=0) ее полная энергия совпадает с кинетической. Для свободной частицы, движущейся вдоль оси х, уравнение Шредингера (21) для стационарных состоя­ний примет вид

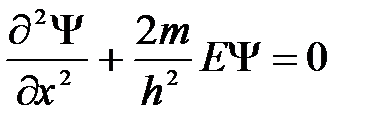( 22 )

Прямой подстановкой можно убедиться в том, что частным решением уравнения (17 ) является функция 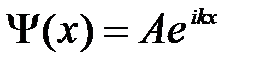, где А = const и k = const, с собственным зна­чением энергии

(23 )

Функция 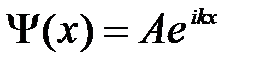пред­ставляет собой только координатную часть волновой функции 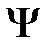(х, t) стационар­ного состояния. Поэтому зависящая от времени волновая функция, согласно (20 ),

(24)

(здесь 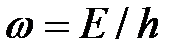и 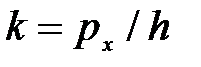). Функция (24) представляет собой плоскую мо­нохроматическую волну де Бройля.

Из выражения (23 ) следует, что за­висимость энергии от импульса

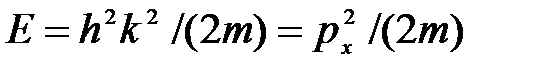
оказывается обычной для нерелятивист­ских частиц. Следовательно, энергия сво­бодной частицы может принимать любые значения (так как волновое число k мо­жет принимать любые значения), т. е. ее энергетический спектр является непрерыв­ным.

Таким образом, свободная квантовая частица описывается плоской монохро­матической волной де Бройля. Этому соответствует не зависящая от времени вероятность обнаружения частицы в данной точке пространства

,

Т.е. все положения свободной частицы в пространстве являются равновероятными.