Квантовые числа
В квантовой механике доказывается, что уравнению Шредингера ( 18 ) удовлетворяют собственные функции 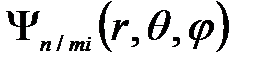 определяемые тремя квантовыми числами: главным
определяемые тремя квантовыми числами: главным 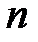 . орбитальным
. орбитальным 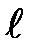 и магнитным
и магнитным 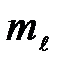 .
.
Главное квантовое число п, согласно ( 19 ), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с единицы:
п= 1,2,3,....
Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. e. не может быть произвольным, а принимает дискретные значения, определяемые формулой
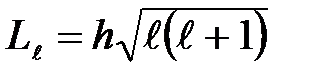 (25)
(25)
где 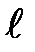 — орбитальное квантовое число, которое при заданном п принимает значения
— орбитальное квантовое число, которое при заданном п принимает значения
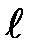 =0,1,..., (п- 1), (26 )
=0,1,..., (п- 1), (26 )
т. e. всего п значений, и определяет момент импульса электрона в атоме.
Из решения уравнений Шредингера следует также, что вектор 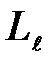 , момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L,, на направление z внешнего магнитного поля принимает квантованные значения, кратные h:
, момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L,, на направление z внешнего магнитного поля принимает квантованные значения, кратные h:
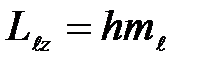 (27 )
(27 )
где т, — магнитное квантовое число, которое при заданном 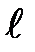 может принимать значения
может принимать значения
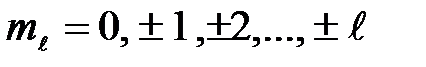 (28)
(28)
т. e. всего 2 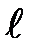 + 1 значений. Таким образом, магнитное квантовое число т, определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2
+ 1 значений. Таким образом, магнитное квантовое число т, определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2 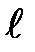 +1 ориентаций.
+1 ориентаций.
Наличие квантового числа т, должно привести в магнитном поле к расщеплению уровня с главным квантовым числом п на 2 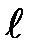 +1 подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщепление энергетических уровней в магнитном поле было обнаружено в 1896 г. голландским физиком П. Зееманом (1865-1945) и получило название эффекта Зеемана. Расщепление уровней энергии во внешнем электрическом поле, тоже доказанное экспериментально, называется эффектом Штарка .
+1 подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщепление энергетических уровней в магнитном поле было обнаружено в 1896 г. голландским физиком П. Зееманом (1865-1945) и получило название эффекта Зеемана. Расщепление уровней энергии во внешнем электрическом поле, тоже доказанное экспериментально, называется эффектом Штарка .
Хотя энергия электрона и зависит только от главного квантового числа п, но каждому собственному значению 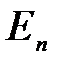 (кроме
(кроме 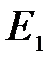 ) соответствует несколько собственных функций
) соответствует несколько собственных функций 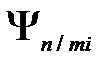 ,отличающихся значениями
,отличающихся значениями 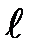 и
и 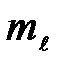 . Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном и орбитальное квантовое число
. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном и орбитальное квантовое число 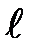 может изменяться от 0 до п—1, а каждому значению
может изменяться от 0 до п—1, а каждому значению 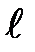 соответствует 2
соответствует 2 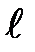 +1 различных значений
+1 различных значений 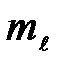 , то число различных состояний, соответствующих данному п, равно
, то число различных состояний, соответствующих данному п, равно
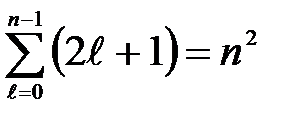 (29)
(29)
В теории Бора априорно, в качестве исходных, вводились те же квантовые числа: главное квантовое число п определяло энергию (или скорость) электрона по круговой (или эллиптической) орбите, орбитальное квантовое число / — размеры орбиты (а следовательно, и момент импульса (mvr) электрона по орбите), магнитное квантовое число т( — ориентацию орбиты в пространстве. Появление же квантовых чисел и значений, принимаемых ими, в квантовой механике является следствием решений уравнения Шредингера и условий однозначности, непрерывности и конечности, налагаемых на волновую функцию  . Кроме того, поскольку при движении электрона в атоме существенны волновые свойства электрона, квантовая механика вообще отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема.
. Кроме того, поскольку при движении электрона в атоме существенны волновые свойства электрона, квантовая механика вообще отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема.
Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы “размазан” по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема атома. В квантовой механике принимается, что квантовые числа п и 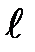 характеризуют размер и форму электронного облака, а квантовое число т, характеризует ориентацию электронного облака в пространстве.
характеризуют размер и форму электронного облака, а квантовое число т, характеризует ориентацию электронного облака в пространстве.
В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами 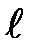 = 0, называют s-состоянием (электрон в этом состоянии называют s-электроном),
= 0, называют s-состоянием (электрон в этом состоянии называют s-электроном), 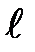 = 1 - р-состоянием,
= 1 - р-состоянием, 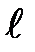 = 2 - d-состоянием,
= 2 - d-состоянием, 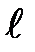 = 3 - f-состоянием .и т. д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях с п = 2 и
= 3 - f-состоянием .и т. д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях с п = 2 и 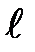 = 0и 1 обозначаются соответственно символами 2s и 2р.
= 0и 1 обозначаются соответственно символами 2s и 2р.
 Рис. 2
Рис. 2
| На рис. 2 для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при п = 1 и п = 2, определяемое 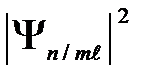 . Как видно из рисунка, оно зависит от п, . Как видно из рисунка, оно зависит от п, 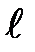 и т,. Так, при и т,. Так, при 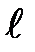 = 0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически симметрична), а для остальных состояний в центре равна нулю и зависит от направления.
Спин электрона
Магнитный момент атома, связанный с движением электрона, пропорционален механическому моменту, поэтому он равен нулю, и магнитное поле не должно оказывать влияние на движение атомов водорода в основном состоянии, т.е. расщепления быть не должно. = 0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически симметрична), а для остальных состояний в центре равна нулю и зависит от направления.
Спин электрона
Магнитный момент атома, связанный с движением электрона, пропорционален механическому моменту, поэтому он равен нулю, и магнитное поле не должно оказывать влияние на движение атомов водорода в основном состоянии, т.е. расщепления быть не должно.
|
Однако в дальнейшем при применении спектральных приборов с большой разрешающей способностью было доказано, что спектральные линии атома водорода обнаруживают тонкую структуру (являются дублетами) даже в отсутствие магнитного поля.
Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д.Уленбек (р.1900) и С.Гаудсмит (1902-1979) предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве,- спином.
Спин электрона (и всех других микрочастиц) – квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе. Наличие у электрона спина вытекает из полученного П.Дираком релятивистского квантового уравнения для электрона.
Если электрону приписывается собственный механический момент импульса (спин) 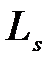 ,то с ним оказывается связанным некоторый собственный магнитный момент
,то с ним оказывается связанным некоторый собственный магнитный момент 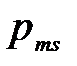 . Согласно общим выводам квантовой механики, спин квантуется по закону
. Согласно общим выводам квантовой механики, спин квантуется по закону
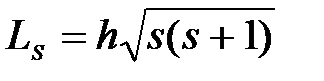
где s – спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция 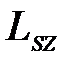 спина квантуется так, что вектор
спина квантуется так, что вектор 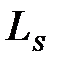 , может принимать
, может принимать 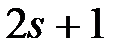 ориентаций. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 = 2, откуда s = ½. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением:
ориентаций. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 = 2, откуда s = ½. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением:
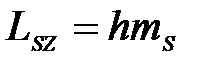
где 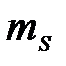 - магнитное спиновое квантовое число; может иметь только два значения:
- магнитное спиновое квантовое число; может иметь только два значения: 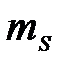 =
= 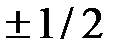
Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.
Дата добавления: 2015-08-11; просмотров: 1497;
