Тема 13. Основы квантовой физики.

Вопросы:

1. Гипотеза де Бройля. Корпускулярно-волновой дуализм.

2. Принцип неопределенности.

3. Волновая функция. Квантовые уравнения движения. Операторы физических величин.

4. Квантовые числа.

5. Многоэлектронный атом. Принцип Паули.

1. Гипотеза де Бройля. Корпускулярно-волновой дуализм

Французский ученый Луи де Бройль (р. 1892), развивая представления о двой­ственной корпускулярно-волновой при­роде света, выдвинул в 1924 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также вол­новыми свойствами.

Итак, согласно де Бройлю, с каждым микрообьектом связываются, с одной сто­роны, корпускулярные характеристики — энергия Е и импульс р, а с другой — волновые характеристики — частота и длина волны . Количественные соот­ношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

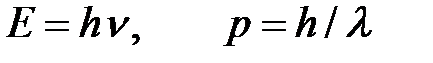(1)

Смелость гипотезы де Бройля заклю­чалась именно в том, что соотношение (1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, со­поставляют волну, длина которой вычис­ляется по формуле де Бройля:

(2)

где р = mv— импульс частицы, имеющей массу т и движущейся со скоростью v.

Вскоре гипотеза де Бройля была под­тверждена экспериментально. В 1927 г. американские физики К. Дэвиссон (1881— 1958) и Л. Джермер (1896-1971) обнару­жили, что пучок электронов, рассеивающийся от естественной дифракцион­ной решетки — кристалла никеля, — дает отчетливую дифракционную картину. Дифракционные максимумы соответство­вали формуле Вульфа — Брэггов , а брэгговская длина волны оказалась в точности равной длине волны, вы­численной по формуле (2). В даль­нейшем формула де Бройля была под­тверждена опытами П. С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (энергия 50 кэВ) через металлическую фольгу (толщиной 1 мкм).

Так как дифракционная картина иссле­довалась для потока электронов, то не­обходимо было доказать, что волновые свойства присущи не только потоку боль­шой совокупности электронов, но и каждо­му электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. советскому физику В. А. Фабриканту (р. 1907). Он показал, что даже в слу­чае столь слабого электронного пучка, когда каждый электрон проходит через устройство независимо от других (про­межуток времени между двумя электро­нами более чем в 10⁴ раз превышал время прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков элек­тронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой части­це в отдельности.

Впоследствии дифракционные явления обнаружили также для нейтронов, про­тонов, атомных и молекулярных пучков. Это окончательно послужило доказа­тельством наличия волновых свойств микрочастиц и позволило описывать дви­жение микрочастиц в виде волнового процесса, характеризующегося определен­ной длиной волны, рассчитываемой по формуле де Бройля (2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких, как электронография и нейтронография, а также к возникновению новой отрасли науки — электронной оп­тики.

Экспериментальное доказательство на­личия волновых свойств микрочастиц привело к выводу о том, что перед нами универсальное явление, общее свой­ство материи. Но тогда волновые свой­ства должны быть присущи и макро­скопическим телам. Почему же они не обнаружены экспериментально? Напри­мер, частице массой 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с 10^{-28 м. Такая длина волны лежит за пределами доступной наблюдению области (периодических структур с периодом} d 10^{-28 м не существует). Поэтому считается, что макроскопические тела проявляют только одну сторону своих свойств} — корпуску­лярную — и не проявляет волновую.

Представление о двойственной корпу­скулярно-волновой природе частиц веще­ства углубляется еще тем, что на час­тицы вещества переносится связь между полной энергией частицы и частотой волн де Бройля:

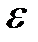= hv. (3)

Это свидетельствует о том, что соот­ношение между энергией и частотой в формуле (3) имеет характер универ­сального соотношения, справедливого как для фотонов, так и для любых других микрочастиц. Справедливость же соотно­шения (3) вытекает из согласия с опытом тех теоретических результатов, которые получены с его помощью в кван­товой механике, атомной и ядерной физи­ке.

Подтвержденная экспериментально ги­потеза де Бройля о корпускулярно-волновом дуализме свойств вещества ко­ренным образом изменила представления о свойствах микрообъектов. Всем микро­объектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании. Современная трактов­ка корпускулярно-волнового дуализма мо­жет быть выражена словами советского физика-теоретика В. А. Фока (1898— 1974): “Можно сказать, что для атомного объекта существует потенциальная воз­можность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и со­стоит дуализм волна — частица. Всякое иное, более буквальное, понимание этого дуализма в виде какой-нибудь модели неправильно.

Некоторые свойства волн де Бройля

Рассмотрим свободно движущуюся со скоростью v частицу массой т. Вычислим для нее фазовую и групповую скорости волн де Бройля. Фазовая скорость

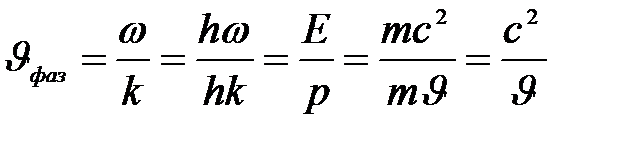(4)

( и 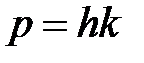, где k = — волно­вое число). Так как с > v, то фазовая скорость волн де Бройля больше скорости света в вакууме. Групповая скорость,

(5)

Для свободной частицы

(6)

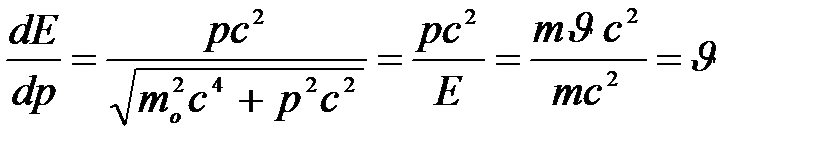(7)

Следовательно, групповая скорость волн де Бройля равна скорости частицы.

Волны де Бройля испытывают диспер­сию. Действительно, подставив в выражение (1) формулу видим, что ско­рость волн де Бройля зависит от длины волны. Это обстоятельство сыграло в свое время большую роль в развитии поло­жений квантовой механики. После уста­новления корпускулярно-волнового ду­ализма делались попытки связать корпу­скулярные свойства частиц с волновыми и рассматривать частицы как “узкие” волновые пакеты , “составлен­ные” из волн де Бройля. Это позволяло, как бы отойти от двойственности свойств частиц. Такая гипотеза соответствовала локализации частицы в данный момент времени в определенной ограниченной области пространства. Аргументом в пользу этой гипотезы являлось и то, что скорость распространения центра пакета (групповая скорость) оказалась, как пока­зано выше, равной скорости частицы. Однако подобное представление частицы в виде волнового пакета (группы волн де Бройля) оказалось несостоятельным из-за сильной дисперсии волн де Бройля, при­водящей к “быстрому расплыванию” (при­мерно 10^-26с!) волнового пакета или даже разделению его на несколько пакетов.

2. Принцип неопределенности

Двойственная корпускулярно-волновая природа частиц вещества, вынуждающая описывать микрочастицы с помощью как волновых, так и корпускулярных пред­ставлений, ставит вопрос о границах применимости понятий классической фи­зики для объектов микромира.

В классической механике всякая частица движется по определенной траектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микрочастицы ввиду наличия у них вол­новых свойств существенно отличаются от классических частиц. Одно из основных различий заключается в том, что микро­частица не имеет траектории, и неправо­мерно говорить об одновременных точных значениях ее координаты и импульса. Это следует из корпускулярно-волнового дуализма. Так, понятие “длина волны в данной точке” лишено физического смыс­ла, а поскольку импульс выражается через длину волны, то отсюда следует, что микрочастица с опре­деленным импульсом имеет полностью неопределенную координату. И наоборот, если микрочастица находится в состоянии с точным значением координаты, то ее импульс полностью неопределенен.

В. Гейзенберг, учитывая волновые свой­ства микрочастиц и связанные с волно­выми свойствами ограничения в их пове­дении, пришел в 1927 г. к выводу, что объект микромира невозможно одно­временно с одинаковой степенью точности характеризовать его координатой и им­пульсом. Согласно соотношению неопре­деленностей Гейзенберга, микрочастица (микрообъект) не может иметь одновре­менно и определенную координату (х, у, z), и определенную соответствующую проек­цию импульса (р р , р ), причем не­определенности в значениях этих величин удовлетворяют условиям

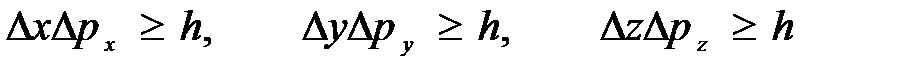(8)

т. e. произведение неопределенностей ко­ординаты и соответствующей ей проекции импульса не может быть меньше величи­ны порядка h.

Из соотношения неопределенностей (8 ) следует, что, например, если микро­частица находится в состоянии с точным значением координаты ( 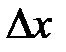= 0), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопре­деленной ( 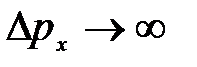), и наоборот. Таким образом, для микрочастицы не су­ществует состояний, в которых ее коорди­наты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременно с одинаковой степенью точности измерить координату и импульс микрообъекта.

Поясним, что соотношение неопределеннос­тей действительно вытекает из волновых свойств микрочастиц. Пусть поток электронов проходит через узкую щель шириной 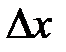расположенную перпендикулярно направлению их движения (рис.1).

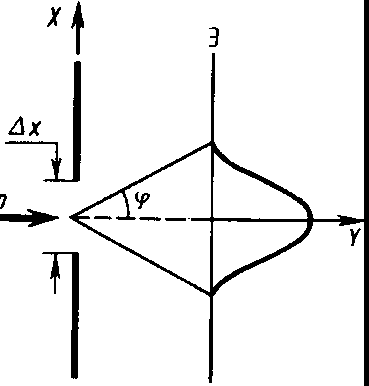
Рис.1

Так как электроны обладают волновыми свойствами, то при размерах щели, сравнимых с длиной волны де Бройля 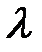электрона, при их прохождении через щель наблюдается дифракция. Дифрак­ционная картина, наблюдаемая на экране (Э), характеризуется главным максимумом, распо­ложенным симметрично оси Y, и побочными максимумами по обе стороны от главного (их не рассматриваем, так как основная доля интенсивности приходится на главный макси­мум).

До прохождения через щель электроны дви­гались вдоль оси Y, поэтому составляющая импульса р_x, =0, так что ∆ р_x = 0, а коорди­ната Х частицы является совершенно неопре­деленной. В момент прохождения электронов через щель их положение в направлении оси Х определяется с точностью до ширины щели, т. e. с точностью х. В этот же момент вследствие дифракции электроны отклоняются от первоначального направления и будут дви­гаться в пределах угла 2 ( φ — угол, соответ­ствующий первому дифракционному миниму­му). Следовательно, появляется неопределен­ность в значении составляющей импульса вдоль оси X, которая, как следует из рис. 1 и формулы (1 ), равна

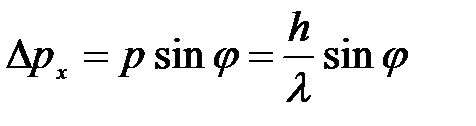( 9 )

Для простоты ограничимся только электро­нами, попадающими на экран в пределах главного максимума. Из теории дифракции известно, что первый минимум соответствует углу φ, удовлетворяющему усло­вию

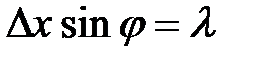(10 )

где 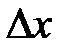- ширина щели, а 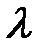— длина волны де Бройля. Из формул ( 9 ) и ( 10 ) получим

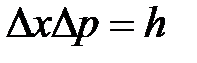(11)

где учтено, что для некоторой, хотя и незначительной части электронов, попадающих за пределы главного максимума, величина 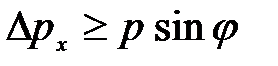. Следовательно, для общего случая получается соотношение

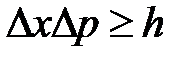
т.е. пришли к соотношению неопределенностей ( 8).

Невозможность одновременно точно определить координату и соответствующую составляющую импульса не связана с несовершенством методов измерения или измерительных приборов, а является следствием специфики микрообъектов, отражающей особенности их объективных свойств, а именно двойственной корпускулярно-волновой природы. Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульс) и наличия у ее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.

Соотношение неопределенностей, отражая специфику физики микрочастиц, позволяет оценить, например, в какой мере можно применять понятия классической механики к микрочастицам, в частности с какой степенью точности можно говорить о траекториях микрочастиц. Известно, что движение по траектории характеризуется в любой момент времени вполне определенными значениями координат и скорости. Выразим соотношение неопределенностей (8) в виде

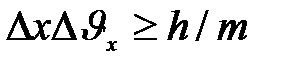(12)

Из этого выражения следует, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Так, например, уже для пылинки массой 10^{-12 кг и линейными размерами 10-6 м, координата которой определена с точностью до 0.01 ее размеров ( 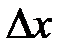= 10-8 м), неопределенность в значении скорости, по ( 12 ) 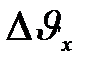= 6.62 10-14} м/с т.е. не будет сказываться при всех скоростях, с которыми пылинка может двигаться. Таким образом, для макроскопических тел их волновые свойства не играют ни какой роли; координата и скорость макротел могут быть одновременно измерены достаточно точно. Это же означает, что для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики.

Применим соотношение неопределенностей к электрону, движущемуся в атоме водорода. Допустим, что неопределенность в определении координаты электрона 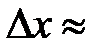10^{-10 м ( порядка самого атома, т.е. можно считать, что электрон принадлежит данному атому).}

Тогда, согласно (12 ), 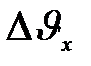=6.62 10^-34/(9.11 10^-31 10^-10) = 7.27 10⁶ м/c.

Используя законы классической физики, можно показать, что при движении электрона вокруг ядра по круговой орбите радиуса 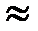0,5-10 ^-10м его скорость 2,3- 10⁶ м/с. Таким обра­зом, величина неопределенности в значе­нии скорости в несколько раз больше самой скорости. Очевидно, что в дан­ном случае нельзя говорить о движении электрона в атоме по определенной траектории, иными словами, для описа­ния движения электрона в атоме нельзя пользоваться законами классической фи­зики.

В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t, т. е. не­определенности в значениях этих величин удовлетворяют условию

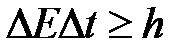( 13 )

Следовательно, система, имеющая среднее время жизни 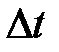, не может быть охарак­теризована определенным значением энер­гии; разброс энергии возрастает с уменьшением среднего времени жизни. Из выражения (13) следует, что частота излученного фотона также должна иметь неопределенность 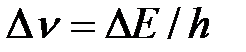, г. е. линии спектра должны характеризоваться часто­той, равной 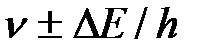. Опыт действительно показывает, что все спектральные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.

Соотношение неопределенностей не­однократно являлось предметом философ­ских дискуссий, приводивших философов к его идеалистическому истол­кованию. Например, по их мнению, соот­ношение неопределенностей, не давая возможности одновременно точно опреде­лить координаты и импульсы (скорости) частиц, устанавливает границу познавае­мости мира, с одной стороны, и суще­ствование микрообъектов вне простран­ства и времени — с другой. На самом деле, соотношение неопределенностей не ставит какого-либо предела познанию микромира, а только указывает, насколько применимы к нему понятия классической механики.

3. Волновая функция. Квантовые уравнения движения. Операторы физических величин

Экспериментальное подтверждение идеи де Бройля об универсальности корпус­кулярно-волнового дуализма, ограничен­ность применения классической механики к микрообъектам, диктуемая соотноше­нием неопределенностей, а также проти­воречие целого ряда экспериментов с при­меняемыми в начале XX в. теориями привели к новому этапу развития кван­товой теории - созданию квантовой меха­ники описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. Ее создание и раз­витие охватывает период с 1900 г. (формулировка Планком квантовой ги­потезы) до 20-х годов XX в; оно связано прежде всего с работами австрийского физика Э. Шредингера (1887—1961), немецкого физика В. Гейзенберга и английского физика П. Ди­рака (р. 1902).

На данном этапе развития возникли но­вые принципиальные проблемы, в част­ности проблема физической природы волн де Бройля. Для выяснения этой проблемы сравним дифракцию световых волн и микрочастиц. Дифракционная кар­тина, наблюдаемая для световых волн, характеризуется тем, что в результате наложения дифрагирующих волн друг на друга в различных точках пространства происходит усиление или ослабление амплитуды колебаний. Согласно волно­вым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. С точки же зрения фотонной теории интенсивность определя­ется числом фотонов, попадающих в дан­ную точку дифракционной картины. Сле­довательно, число фотонов в данной точ­ке дифракционной картины определяет­ся квадратом амплитуды световой волны, в то время как для одного фотона ква­драт амплитуды определяет вероятность попадания фотона в ту или иную точку.

Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков микрочастиц, рассеянных или отражен­ных по различным направлениям,— в одних направлениях наблюдается боль­шее число частиц, чем в других. Наличие максимумов в дифракционной картине с точки зрения волновой теории оз­начает, что эти направления соответ­ствуют наибольшей интенсивности волн де Бройля. С другой стороны, интенсив­ность волн де Бройля оказывается боль­ше там, где имеется большее число ча­стиц, т. е. интенсивность волн де Брой­ля в данной точке пространства опре­деляет число частиц, попавших в эту точку. Таким образом, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой части­цы попадают в те места, где ин­тенсивность волн де Бройля наибольшая.

Необходимость вероятностного подхо­да к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Можно ли волны де Бройля истолковывать как волны вероятности, т. е. считать, что вероят­ность обнаружить микрочастицу в раз­личных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно хотя бы потому, что тогда вероятность обнару­жить частицу в некоторых точках про­странства может быть отрицательна, что не имеет смысла.

Чтобы устранить эти трудности, не­мецкий физик М. Борн (1882-1970) в 1926 г. предположил, что по волно­вому закону меняется не сама вероят­ность, а некая величина, названная амплитудой вероятности, обозначаемая 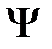(х, у, z, t). Эту величину называют также волновой функцией (или 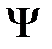-фун­кцией). Амплитуда вероятности может быть комплексной, и вероятность W про­порциональна квадрату ее модуля:

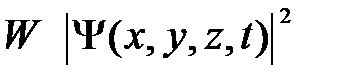( 14 )

Таким образом, описание состояния мик­рообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функ­ции (квадрат модуля амплитуды волн де Бройля) определяет вероятность на­хождения частицы в момент времени t в об­ласти с координатами х и х + dx, у и у + dy, z и z + dz.

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому — с помощью волновой функ­ции, которая является основным носителем информации об их корпускулярных и вол­новых свойствах. Вероятность нахожде­ния частицы в элементе объема dV равна

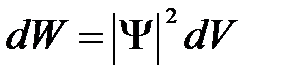( 15 )

где величина

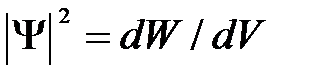
(квадрат модуля 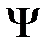-функции) имеет смысл плотности вероятности. Таким образом, физический смысл имеет не сама 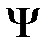-функ­ция, а квадрат ее модуля , которым задается интенсив­ность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна

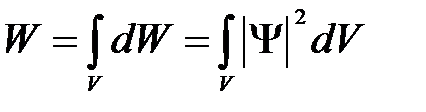
Поскольку 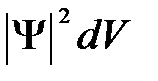определяется как ве­роятность, необходимо волновую фун­кцию 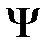нормировать так, чтобы ве­роятность W достоверного события об­ращалась в единицу, если за объем V принять бесконечный объем всего про­странства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей

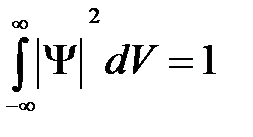( 16 )

где данный интеграл ( 16 ) вычисляет­ся по всему бесконечному пространству, т. е. по координатам х, у, z от 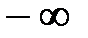до 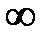. Таким образом, условие ( 16 ) говорит об объективном существовании частицы во времени и пространстве.

Чтобы волновая функция являлась объ­ективной характеристикой состояния ми­крочастиц, она должна удовлетворять ряду ограничительных условий. Функция 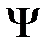, характеризуя вероятность обнаружения действия микрочастицы в элементе объ­ема, должна быть конечной (вероятность не может быть больше единицы), од­нозначной (вероятность не может быть не однозначной величиной) и непрерывной (вероятность не может изменяться скач­ком).

Волновая функция удовлетворяет прин­ципу суперпозиции: если система может находиться в различных состояниях, опи­сываемых волновыми функциями 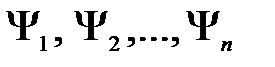, то она также может нахо­диться в состоянии 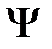, описываемом ли­нейной комбинацией этих функций:

где 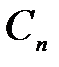(n =1,2,...)— некоторые комплекс­ные числа. Сложение волновых функций (амплитуд вероятностей), а не вероят­ностей (квадратов волновых функций) принципиально отличает квантовую тео­рию от классической статистической тео­рии, в которой для независимых собы­тий справедлива теорема сложения веро­ятностей.

Зная волновую функцию в квантовой механике, вычисляют средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние <r> электрона от ядра вы­числяют по формуле

Где интегрирование производится, как и в случае ( 16 ).

Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением дви­жения в квантовой механике, описывающим движение микрочастиц в различ­ных силовых полях, должно быть урав­нение, из которого бы вытекали наблю­даемые на опыте волновые свойства ча­стиц. Основное уравнение должно быть уравнением относительно волновой фун­кции (х, у, z, t), так как именно она, или, точнее, величина , определяет вероятность пребывания частицы в момент времени t в объеме dV, т.е. в области с координатами х и х + dx, у и у 4-+ dy, z и z+dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравне­нию, описывающему электромагнитные волны.

Основное уравнение нерелятивистской квантовой механики сформулировано Э. Шредингером (1926). Уравнение Шре­дингера, как и все основные уравнения физики (например, уравнение Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правиль­ность этого уравнения подтверждается согласием с опытом получаемых с его по­мощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид

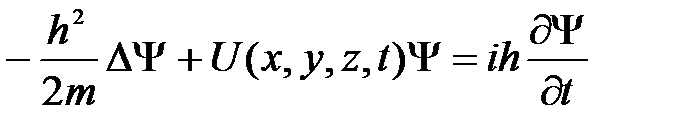(17 )

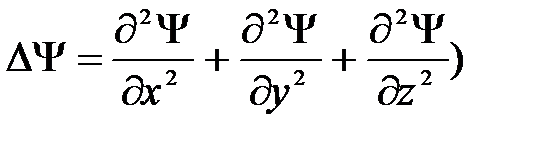где , m — масса частицы, - оператор Лапласа ( , i-мнимая единица, U (х, у, z, t)— потенциальная энергия частицы в си­ловом поле, в котором частица движется.

Уравнение ( 17 ) справедливо для лю­бой частицы, движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью . Оно дополня­ется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной ; 2) производные 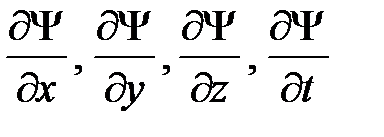должны быть непрерывны; 3) функция должна быть интегрируема; это условие в простейших случаях сводится к условию норми­ровки вероятностей ( ).

Чтобы прийти к уравнению Шредингера, рассмотрим свободно движущуюся частицу, которой, согласно идее де Бройля, сопостав­ляется плоская волна. Для простоты рассмот­рим одномерный случай. Уравнение плоской волны, распространяющейся вдоль оси х, име­ет вид

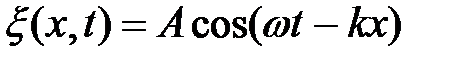, или комплексной записи

Следовательно, плоская волна де Бройля имеет вид

(18 )

(учтено, что 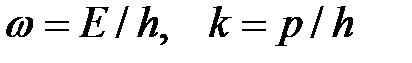). Так как физи­ческий смысл имеет только , знак “минус” в экспоненте (18) несущественен. Тогда

Откуда

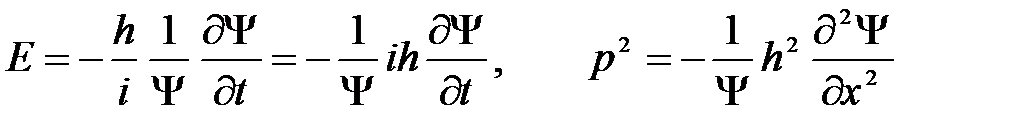(19 )

Используя взаимосвязь между энергией 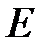и им­пульсом получим дифференциальное урав­нение

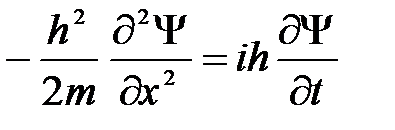
которое совпадает с уравнением ( 17 ) для случая U = 0 (мы рассматривали свободную частицу).

Если частица движется в силовом поле, характеризуемом потенциальной энергией U, то полная энергия Е складывается из кинети­ческой и потенциальной энергий. Проводя аналогичные рассуждения и используя взаимо­связь между 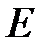и р для данного случая , придем к дифференциальному уравнению, совпадающему с ( 17 ).

Приведенные рассуждения не должны восприниматься как вывод уравнения Шре­дингера. Они лишь поясняют, как можно прийти к этому уравнению. Доказатель­ством правильности уравнения Шредин­гера является согласие с опытом тех выводов, к которым оно приводит.

Уравнение ( 1 ) является общим урав­нением Шредингера. Его также называют уравнением Шредингера, зависящим от времени.