Уравнение Шредингера для стационарных состояний.

Для многих физических явле­ний, происходящих в микромире, уравне­ние (17) можно упростить, исключив зависимость 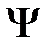от времени. Это возмож­но, если силовое поле, в котором ча­стица движется, стационарно, т. е. фун­кция U=U{x,y,z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение урав­нения Шредингера может быть представ­лено в виде произведения двух функций, одна из которых есть функция только координат, другая — только времени, при­чем зависимость от времени выражается множителем 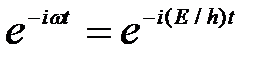, так что

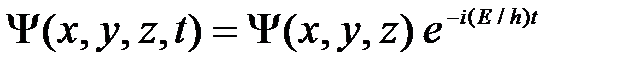(20)

где Е — полная энергия частицы, постоян­ная в случае стационарного поля. Под­ставляя (20) в ( 17 ), получим

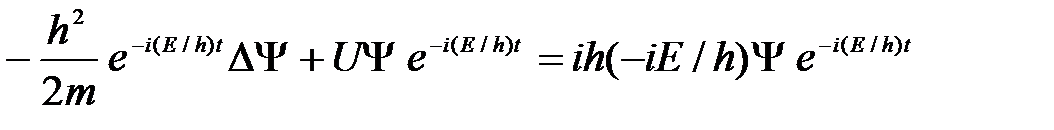
откуда после деления на общий множи­тель и соответствующих преоб­разований придем к уравнению, опреде­ляющему функцию :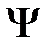

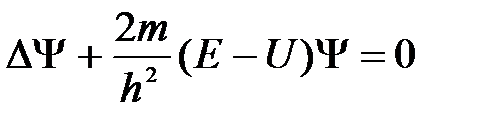(21)

Уравнение (21) называется уравнением Шредингера для стационарных состояний. Мы проанализируем только это уравне­ние и для краткости в дальнейшем будем называть его просто уравнением Шредингера.

В уравнение Шредингера ( 21 ) в ка­честве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют решения не при лю­бых значениях параметра, а лишь при определенных значениях Е. Эти значения энергии называются собственными. Реше­ния же, которые соответствуют собствен­ным значениям энергии, называются соб­ственными функциями. Собственные зна­чения Е могут образовывать как непре­рывный, так и дискретный ряд. В пер­вом случае говорят о непрерывном, или сплошном, спектре, во втором - о дискрет­ном спектре.