Многоэлектронный атом. Принцип Паули
Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной. Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули).
Из сформулированного положения вытекает и элементарная формулировка принципа Паули, которая и была введена им в квантовую теорию (1925) еще до построения квантовой механики: в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.
Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:
главного п (п = 1, 2, 3, ...),
орбитального 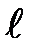 (
( 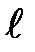 = 0, 1, 2, ..., п— 1),
= 0, 1, 2, ..., п— 1),
магнитного ml (ml=- 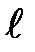 , ..., —1, 0, +1,...,+
, ..., —1, 0, +1,...,+ 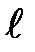 ) и
) и
магнитного спинового тs, (тs, = + 1/2, -1/2).
Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел п, 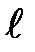 , ml и тs,, т.
, ml и тs,, т.
Z(n, 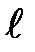 , ml, тs,) = 0 или 1,
, ml, тs,) = 0 или 1,
где Z{n, 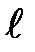 , ml, тs,) — число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел: п,
, ml, тs,) — число электронов, находящихся в квантовом состоянии, описываемом набором четырех квантовых чисел: п, 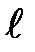 , ml и тs . Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.
, ml и тs . Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.
Данному 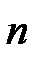 соответствует п2 различных состояний, отличающихся значениями
соответствует п2 различных состояний, отличающихся значениями 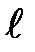 и тl,. Квантовое число т, может принимать лишь два значения (± 1/2). Поэтому Z(n) — максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом п, равно 2п2, так как
и тl,. Квантовое число т, может принимать лишь два значения (± 1/2). Поэтому Z(n) — максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом п, равно 2п2, так как
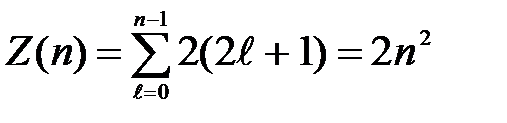
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число п, называют электронной оболочкой. В каждой из оболочек электроны подразделяются по подоболочкам, соответствующим данному значению 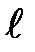 . Поскольку орбитальное квантовое число принимает значения от О до n—1, число подоболочек равно порядковому номеру п оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным
. Поскольку орбитальное квантовое число принимает значения от О до n—1, число подоболочек равно порядковому номеру п оболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным 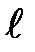 равно 2(2
равно 2(2 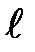 + 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 1.
+ 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 1.
Таблица 1
| Главное квантовое число n | |||||||||||||||
| Символ оболочки | K | L | M | N | O | ||||||||||
| Масмаль-ное число электронов и оболочек | |||||||||||||||
| Орбиталь-ное кватовое число | |||||||||||||||
| Символ подоболочки | 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
| Масмальное число электрнов в подобо-лочке |
Тема 14. Элементы квантовой механики,
Дата добавления: 2015-08-11; просмотров: 1036;
