Алгебраическая форма записи комплексного числа.
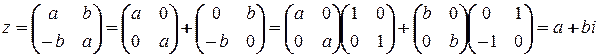 ,
,
где 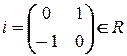 .
.
Определение. 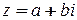 - алгебраическая форма записи комплексного числа, причем единственная.
- алгебраическая форма записи комплексного числа, причем единственная.
Предложение 1. 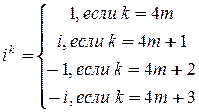 для любого
для любого  .
.
Определим действия сложения и умножения на множестве комплексных чисел, заданных в алгебраической форме:
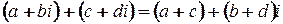
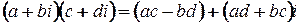
Определение.Сопряженным к комплексному числу 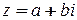 называется комплексное число
называется комплексное число 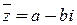 .
.
Свойства сопряженных комплексных чисел:
1. 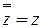 ;
;
2. 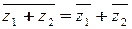 ;
;
3. 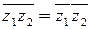 ;
;
4. 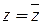 т.т.т.,к.
т.т.т.,к. 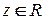 ;
;
5. 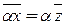 для любого
для любого 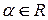 .
.
Определение.Нормой комплексного числа 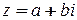 называется число
называется число 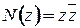 .
.
Замечание. 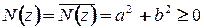 .
.
Свойства нормы:
1. 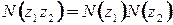 ;
;
2. 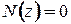 т.т.т.,к.
т.т.т.,к. 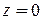 ;
;
3. 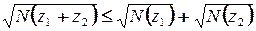 ;
;
4. если  , то
, то 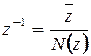 .
.
Дата добавления: 2015-08-21; просмотров: 1609;
