Доказательство. Проверим, что подкольцо кольца , а, следовательно, само образует кольцо.

Проверим, что 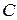подкольцо кольца 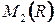, а, следовательно, само образует кольцо.

.

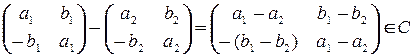
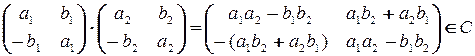Нетрудно устанавливается, что в 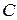умножение коммутативно и ассоциативно.

Остается покакать, что в 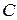каждый ненулевой элемент обратим.

Пусть 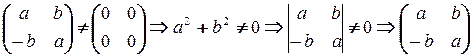- обратима в 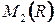. Тогда .

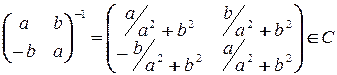Таким образом, 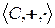- поле.

что и требовалось доказать.

Теорема 2.Поле действительных чисел изоморфно вкладывается в поле комплексных.