Доказательство. Рассмотрим соответствие по правилу для всех .

Рассмотрим соответствие 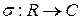по правилу 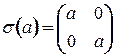для всех .

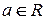Очевидно, что - всюдуопределено и однозначно, а, следовательно, - отображение.

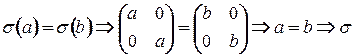- инъективное отображение.

Покажем, что - гомоморфизм.

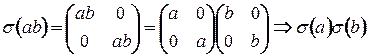
Таким образом, - инъективный гомоморфизм, а, значит, 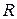изоморфно вкладывается в .

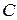что и требовалось доказать.