Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.

Теорема 7. 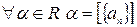т.т.т., к. 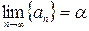, иными словами всякая фундаментальная последовательность рациональных чисел сходится в поле действительных чисел.

Доказательство.

Необходимость.

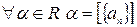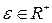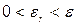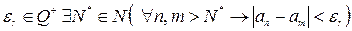Пусть . Возьмем такое, что , где (в силу фундаментальности последовательности 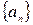). Тогда 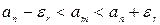. Согласно леммам 1, 2, имеем, что 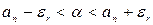, следовательно, 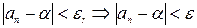. Таким образом, .

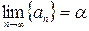Достаточность.

Пусть 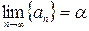. Покажем, что 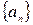- ф.п.р.ч.

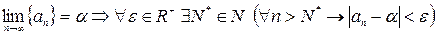. Поскольку между действительными числам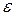и и 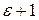найдется положительной рациональное число 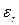. Тогда 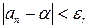. Оценим 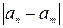, где :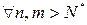

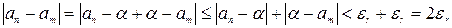. Таким образом, последовательность рациональных чисел 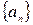фундаментальна, а, значит, порождает некоторый класс эквивалентности 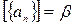. Остается доказать, что 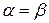. Возможны случаи:

1. .

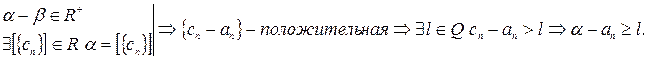Последнее противоречит условию 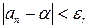, следовательно, данный случай невозможен.

2. .

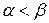Последнее противоречит условию 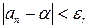, следовательно, данный случай невозможен.

3. 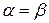. Единственно возможный случай.

что и требовалось доказать.

Следствие. Для того, чтобы последовательность рациональных чисел имела в поле действительных чисел предел необходимо и достаточно, чтобы она была фундаментальной.