Упорядоченность поля действительных чисел.
Теорема 4.Поле действительных чисел упорядоченное.
Доказательство.
Рассмотрим подмножество 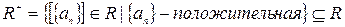 . Нетрудно проверить аксиомы положительного конуса для
. Нетрудно проверить аксиомы положительного конуса для 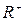 .
.
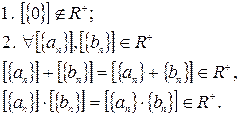
Последнее справедливо, поскольку сумма и произведение положительных последовательностей также являются последовательностями положительными.
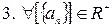 возможен один из трех случаев:
возможен один из трех случаев:
§ 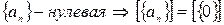 ,
,
§ 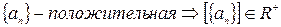 ,
,
§ 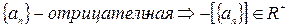 .
.
что и требовалось доказать.
Следствие 1. Бинарное отношение < на 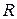 , определенное по правилу
, определенное по правилу 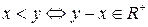 является строгим линейным порядком и удовлетворяет свойствам 1.-6. (см. теорему об упорядоченных кольцах).
является строгим линейным порядком и удовлетворяет свойствам 1.-6. (см. теорему об упорядоченных кольцах).
Следствие 2. Бинарное отношение 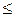 на
на 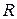 , определенное по правилу
, определенное по правилу 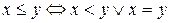 является линейным порядком.
является линейным порядком.
Лемма 1. Если 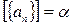 и
и 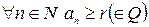 , то
, то 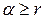 .
.
Дата добавления: 2015-08-21; просмотров: 855;
