I. Числовая последовательность, предел последовательности
Определение. Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана последовательность
x1, х2, …, хn = {xn}
Общий элементпоследовательности является функцией от n xn = f(n)
Рассмотрим последовательность {xn} = 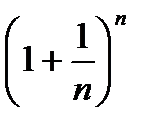 .
.
Если последовательность {xn} монотонная и ограниченная, то она имеет конечный предел.
По формуле бинома Ньютона:
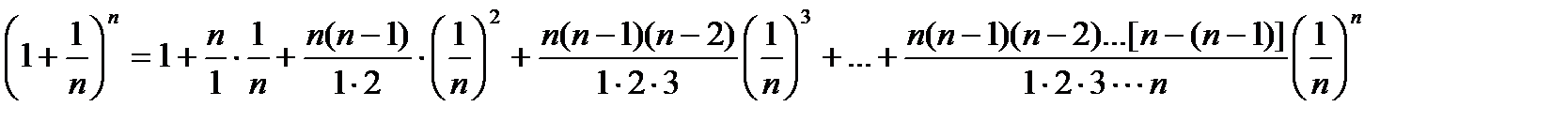 или, что то же самое
или, что то же самое
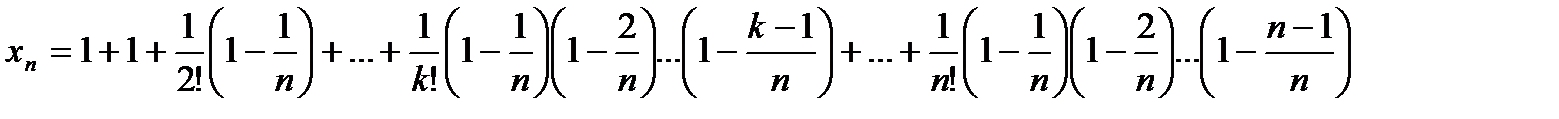
Покажем, что последовательность {xn} – возрастающая. Действительно, запишем выражение xn+1 и сравним его с выражением xn:
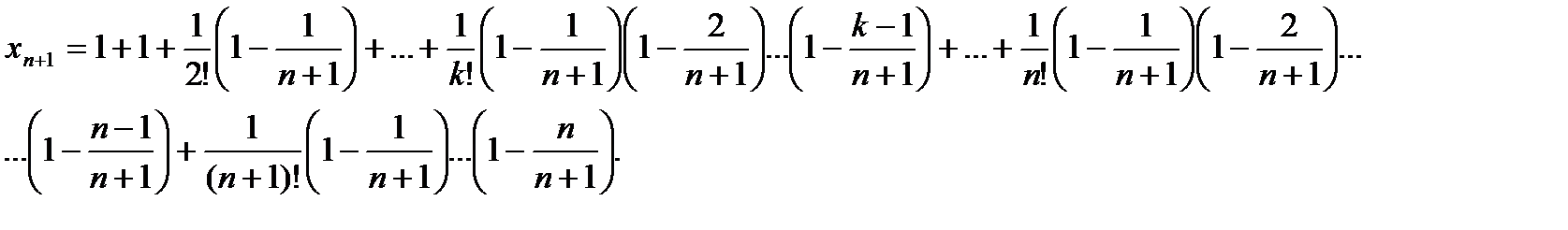 Каждое слагаемое в выражении xn+1 больше соответствующего значения xn, и, кроме того, у xn+1 добавляется еще одно положительное слагаемое. Таким образом, последовательность {xn} возрастающая.
Каждое слагаемое в выражении xn+1 больше соответствующего значения xn, и, кроме того, у xn+1 добавляется еще одно положительное слагаемое. Таким образом, последовательность {xn} возрастающая.
Докажем теперь, что при любом n ее члены не превосходят трех: xn < 3.
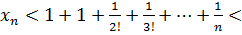 1+1+
1+1+ 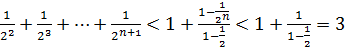 – это есть убывающая геометрическая прогрессия со знаменателем прогрессии q=
– это есть убывающая геометрическая прогрессия со знаменателем прогрессии q=  .
.
Итак, последовательность 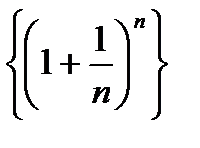 - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой , т.е.
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой , т.е. 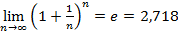 .
.
Дата добавления: 2015-08-11; просмотров: 2081;
