Общие свойства
В математическом анализе исходят из определения функции по Лобачевскому и Дирихле. Если каждому числу х из некоторого множества F чисел в силу какого-либо. закона приведено в соответствие число у, то этим определена функция от одного переменного х и в общем записывается y=f(x).».
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции. Символом f(x) обозначают значение функции, соответствующее значению аргумента, равному х.
Аналогично определяется функция, зависящая от нескольких переменных y=f(x)=f( 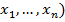 ,
,
где х= (х 1, ..., х п) - точка n-мерного пространства; рассматривают также функции от точек
x=(x1, х2,...) некоторого бесконечномерного пространства, которые, впрочем, чаще называют функционалами.
Числовая функция определена на множестве D действительных чисел, если каждому значению переменной х поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Способы задания функции:
1. аналитический способ (функция задается с помощью математической формулы);
2. табличный способ (функция задается с помощью таблицы);
3. описательный способ (функция задается словесным описанием);
4. графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
1 Нули функции
Нуль функции – такое значение аргумента, при котором значение функции равно нулю 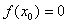 .
.
2. Промежутки знакопостоянства функции
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
3 Возрастание (убывание) функции.
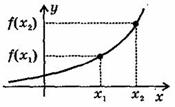
Возрастающаяв некотором промежутке функция - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Функцияу = f (x)называется возрастающейна интервале (а; b), если для любых x1 и x2 из этого интервала таких, что x1< x2 , справедливо неравенство f(x1)<f(x2).
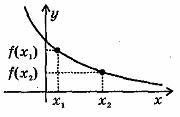
Убывающая в некотором промежутке функция - функция, у которой большему значению аргументаиз этого промежутка соответствует меньшее значение функции.
Функцияу =f (x)называется убывающейна интервале (а; b), если для любых x1 и x2 из этого интервала таких, что x1< x2, справедливо неравенство f(x1)>f(x2).
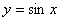
Дата добавления: 2015-08-11; просмотров: 1358;
