Квазистационарные цепи переменного тока
Переменным током называют электрический ток, изменяющийся со временем. К переменному току относят различные виды импульсных, периодических и квазипериодических токов. Наиболее употребителен переменный ток, сила которого I меняется во времени по гармоническому закону. В электротехнике и довольно часто в радиотехнике реализуются квазистационарные цепи переменного тока, для которых мгновенные значения силы тока во всех сечениях цепи одинаковы ввиду медленного их изменения, в то время как электромагнитные возмущения по цепи распространяются со скоростью света. Для мгновенных значений силы и напряжения квазистационарных токов справедливы законы постоянного тока: закон Ома и закон Джоуля–Ленца. Ранее, рассматривая цепь постоянного тока мы получили закон Ома для неоднородного участка цепи (см. форму- лу (56.5)). В случае квазистационарных токов необходимо учитывать наличие явления электромагнитной индукции, которое вызывает появление добавочной ЭДС вследствие неравной нулю правой части второго уравнения Максвелла: 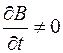 . Этой добавочной электродвижущей силой в данном случае будет ЭДС самоиндукции
. Этой добавочной электродвижущей силой в данном случае будет ЭДС самоиндукции 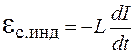 . Поэтому закон Ома для квазистационарных процессов запишется в виде
. Поэтому закон Ома для квазистационарных процессов запишется в виде
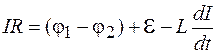 . (108.1)
. (108.1)
Квазистационарные токи и поля существуют по двум причинам. Во-первых, среди нестационарных токов есть такие, которые подобно стационарным протекают в замкнутых цепях и в каждом сечении любого неразветвленного участка цепи имеют одну и ту же силу тока. Во-вторых, область, в которой исследуется влияние полей, оказывается настолько ограниченной по размерам, что электромагнитные возмущения (волны) преодолевают ее практически мгновенно. Строго говоря, в любой точке пространства и в каждый момент времени переменное поле соответствует не тому распределению зарядов, которое имеет место в данный момент времени, а тому, которое было несколько раньше. Это запаздывающее согласование обусловлено фундаментальным свойством природы – ограниченностью скорости передачи любых материальных воздействий. В пустом пространстве электромагнитные возмущения (волны) распространяются со скоростью света. По этой причине полю, возникшему около зарядов, нужно некоторое время, чтобы достичь выбранной точки. С этим однако можно не считаться, если за время распространения поля распределение зарядов изменяется пренебрежимо мало. Тогда и будет выполняться условие квазистационарности тока. При этом существенно то, что квазистационарным поле может быть лишь в ограниченной области; на достаточно больших расстояниях необходимо учитывать запаздывание.
Большинство пассивных электрических цепей работает в линейном режиме, когда справедлив принцип суперпозиции. Форма гармонической переменной тока в такой цепи не искажается, в то время как наличие нелинейных элементов (трансформаторов, нелинейных преобразователей, диодов и т. п.) вызывает искажение гармонических сигналов, у них появляются высокочастотные составляющие. Квазистационарные цепи с сосредоточенными параметрами могут быть составлены как комбинации элементов: катушек индуктивности L, конденсаторов С и резисторов R. В линейных режимах величины L, C, R либо постоянны, либо зависят от времени; в нелинейных режимах они являются функциями силы тока.
С ростом частоты 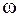 квазистационарное приближение перестает быть справедливым и для расчета цепей переменного тока необходимо обращаться непосредственно к уравнениям Максвелла.
квазистационарное приближение перестает быть справедливым и для расчета цепей переменного тока необходимо обращаться непосредственно к уравнениям Максвелла.
1. Цепь, содержащая активное сопротивление (рис. 108.1, а)
Активным называют сопротивление, потребляющее энергию электрического тока, которая в соответствии с законом Джоуля–Ленца превращается в тепловую энергию. Активным является сопротивление резисторов. Пусть на резистор подано переменное напряжение, мгновенное значение которого определяется формулой
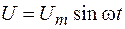 , (108.2)
, (108.2)
где 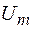 – амплитуда напряжения. По закону Ома,
– амплитуда напряжения. По закону Ома,
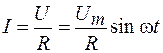 , (108.3)
, (108.3)
где 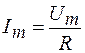 – амплитуда силы тока в цепи резистора. Тогда формулу (108.3) можно записать в виде
– амплитуда силы тока в цепи резистора. Тогда формулу (108.3) можно записать в виде
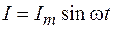 . (108.4)
. (108.4)
 |
Сопоставляя выражения (108.2) и (108.4), можно сделать вывод, что в цепи, содержащей активное сопротивление, ток и напряжение изменяются в одинаковых фазах. Векторная диаграмма амплитудных значений тока
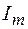 и напряжения
и напряжения 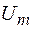 представлена на рисунке 108.1, б.
представлена на рисунке 108.1, б.
2. Цепь, содержащая конденсатор (рис. 108.2, а)
При включении конденсатора в цепь переменного тока происходит его периодическая перезарядка с частотой 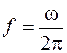 . По цепи при этом протекает электрический ток.
. По цепи при этом протекает электрический ток.
 |
Для зарядки и разрядки конденсатора требуется время, поэтому конденсатор в цепи переменного тока обладает некоторым сопротивлением
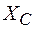 . Это сопротивление является реактивным, не потребляющим энергию электрического тока. В первую четверть периода конденсатор заряжается и запасает энергию, во вторую четверть разряжается и возвращает энергию в электрическую цепь. Далее все повторяется. Следовательно, в конденсаторе не происходит рассеивания энергии электрического тока.
. Это сопротивление является реактивным, не потребляющим энергию электрического тока. В первую четверть периода конденсатор заряжается и запасает энергию, во вторую четверть разряжается и возвращает энергию в электрическую цепь. Далее все повторяется. Следовательно, в конденсаторе не происходит рассеивания энергии электрического тока.
В любой момент времени заряд на обкладках конденсатора
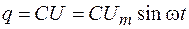 . (108.5)
. (108.5)
Так как 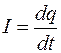 , то на основании формулы (108.5) получаем:
, то на основании формулы (108.5) получаем:
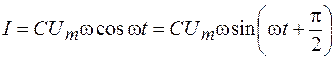 . (108.6)
. (108.6)
Амплитуда силы тока в цепи контура равна
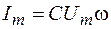 . (108.7)
. (108.7)
Объединяя формулы (108.6) и (108.7), имеем
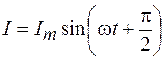 . (108.8)
. (108.8)
Падение напряжения на конденсаторе равно
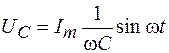 . (108.9)
. (108.9)
Сравнивая выражения (108.8) и (108.9), заключаем, что напряжение в цепи, содержащей конденсатор, отстает по фазе от тока на 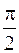 . Векторная диаграмма для этого случая представлена на рисунке 108.2, б.
. Векторная диаграмма для этого случая представлена на рисунке 108.2, б.
Из формулы (108.7) видно, что 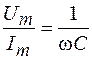 . На основании закона Ома делаем вывод, что это выражение определяет сопротивление конденсатора
. На основании закона Ома делаем вывод, что это выражение определяет сопротивление конденсатора 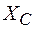 в цепи переменного тока, т. е.
в цепи переменного тока, т. е.
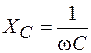 . (108.10)
. (108.10)
Для постоянного тока 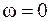 , поэтому
, поэтому 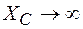 , а это означает, что постоянный ток не может течь через конденсатор.
, а это означает, что постоянный ток не может течь через конденсатор.
3. Цепь, содержащая катушку индуктивности (рис. 108.3, а)
 |
При протекании переменного тока через катушку индуктивности в ней возникает ЭДС самоиндукции
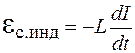 , которая создает индукционный ток, препятствующий изменению основного тока в цепи. Поэтому катушка индуктивности обладает сопротивлением
, которая создает индукционный ток, препятствующий изменению основного тока в цепи. Поэтому катушка индуктивности обладает сопротивлением 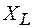 переменному току.
переменному току.
В любой момент времени
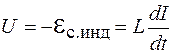 . (108.11)
. (108.11)
Из формул (108.2) и (108.11) имеем
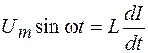 .
.
Отсюда получаем:
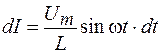 .
.
Интегрируя это выражение, находим:
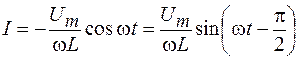 , (108.12)
, (108.12)
где амплитуда силы тока
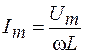 . (108.13)
. (108.13)
Объединяя выражения (108.12) и (108.13), получаем:
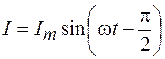 . (108.14)
. (108.14)
Падение напряжения на катушке индуктивности равно
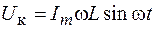 . (108.15)
. (108.15)
Сравнивая выражения (108.2) и (108.14), заключаем, что напряжение в цепи, содержащей катушку индуктивности, опережает по фазе ток на 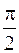 . Векторная диаграмма показана на рисунке 108.3, б.
. Векторная диаграмма показана на рисунке 108.3, б.
Из формулы (108.13) видно, что  . На основании закона Ома делаем вывод, что это выражение определяет сопротивление катушки индуктивности
. На основании закона Ома делаем вывод, что это выражение определяет сопротивление катушки индуктивности 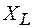 в цепи переменного тока, т. е.
в цепи переменного тока, т. е.
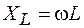 . (108.16)
. (108.16)
Индуктивное сопротивление не потребляет энергии электрического тока, т. е. является реактивным. В первую четверть периода при возрастании тока в магнитном поле катушки запасается энергия. В следующую четверть периода при убывании тока энергия магнитного поля возвращается в электрическую цепь. Далее все повторяется. Следовательно, в катушке индуктивности не происходит рассеивания энергии электрического тока. Говорят, что индуктивность – недиссипативный элемент, в ней не растрачивается (не "диссипирует") электрическая энергия. То же самое относится и к конденсатору. Однако не следует забывать, что катушки изготавливаются из провода, обладающего некоторым активным сопротивлением, в котором происходит выделение джоулева тепла.
Таким образом, в цепи переменного тока резисторы обладают активным сопротивлением, конденсаторы и катушки индуктивности – реактивным.
4. Цепь, содержащая последовательно соединенные резистор, катушку индуктивности и конденсатор (рис. 108.4, а)
В этом случае полное сопротивление цепи переменному току (импеданс цепи) Z определяется выражением
 , (108.17)
, (108.17)
а сила тока в цепи
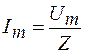 . (108.18)
. (108.18)
Формулу (108.18) называют законом Ома для переменного тока.
При пропускании переменного тока по такой цепи на ее элементах возникают падения напряжения: 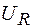 ,
, 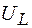 и
и 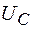 . Векторная диаграмма амплитуд падений напряжений на резисторе (
. Векторная диаграмма амплитуд падений напряжений на резисторе ( 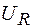 ), катушке индуктивности (
), катушке индуктивности ( 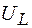 ) и конденсаторе (
) и конденсаторе ( 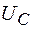 ) представлена на рисунке 108.4, б. Разность фаз
) представлена на рисунке 108.4, б. Разность фаз  между током и напряжением определяется отношением реактивного сопротивления к активному:
между током и напряжением определяется отношением реактивного сопротивления к активному:
 |
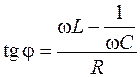 . (108.19)
. (108.19)
Дата добавления: 2015-08-08; просмотров: 4083;
